Đề thi Đại học môn Toán khối A và A1 năm 2012
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 713
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x4 – 2(m + 1)x2 + m2 (1), với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 0. b) Tìm m để đồ thị của hàm số (1) có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông.
Câu 2: Giải phương trình √3sin2x + cos2x + 2cosx – 1 .
Câu 3: Giải hệ phương trình 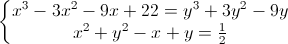 (x, y ∈ R).
(x, y ∈ R).
Câu 4: Tính tích phân I = 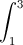
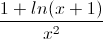 dx.
dx.
Câu 5: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 600. Tính thể tích của khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SA và BC theo a.
Câu 6: Cho các số thực x, y, z thỏa mãn điều kiện x + y + z = 0. Tìm giá trị nhỏ nhất của biểu thức P = 3|x – y| + 3|y – z| + 3|z – x| - 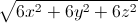 .
.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm của cạnh BC, N là điểm trên cạnh CD sao cho CN = 2ND. Giả sử M(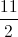 ;
;  ) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
Câu 8: Trong không gian với hệ tạo độ Oxyz, cho đường thẳng d : 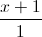 =
= 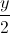 =
= 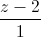 và điểm I(0; 0; 3). Viết phương trình mặt cầu (S) có tâm I và cắt d tại hai điểm A, B sao cho tam giác IAB vuông tại I.
và điểm I(0; 0; 3). Viết phương trình mặt cầu (S) có tâm I và cắt d tại hai điểm A, B sao cho tam giác IAB vuông tại I.
Câu 9: Cho n là số nguyên dương thỏa mãn 5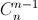 =
= 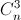 . Tìm số hạng chứa x5 trong khai triển nhị thức Niu – tơn của (
. Tìm số hạng chứa x5 trong khai triển nhị thức Niu – tơn của (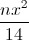 -
-  )n , x ≠ 0.
)n , x ≠ 0.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ): x2 + y2 = 8. Viết phương trình chính tắc của Elip (E), biết rằng (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành bốn đỉnh của một hình vuông.
Câu 11: Trong không gian với hệ tạo độ Oxyz, cho đường thẳng d : 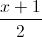 =
= 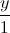 =
= 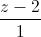 , mặt phẳng (P): x + y – 2z + 5 = 0 và điểm A(1; - 1; 2). Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt tại M và N và A là trung điểm của đoạn thẳng MN.
, mặt phẳng (P): x + y – 2z + 5 = 0 và điểm A(1; - 1; 2). Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt tại M và N và A là trung điểm của đoạn thẳng MN.
Câu 12: Cho số phức z thỏa mãn 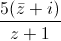 = 2 – i. Tính môđun của số phức w = 1 + z + z2.
= 2 – i. Tính môđun của số phức w = 1 + z + z2.
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
11 | 12 | 92% | 3.95 |
| 2 |
|
8 | 9 | 89% | 3.28 |
| 3 |
|
8 | 9 | 89% | 128.05 |
| 4 |
|
8 | 9 | 89% | 3.28 |
| 5 |
|
8 | 9 | 89% | 9.13 |
| 6 |
|
8 | 9 | 89% | 1.23 |
| 7 |
|
8 | 9 | 89% | 4.78 |
| 8 |
|
7 | 8 | 88% | 145.2 |
| 9 |
|
7 | 9 | 78% | 2.13 |
| 10 |
|
6 | 7 | 86% | 3.3 |
| 11 |
|
6 | 7 | 86% | 107 |
| 12 |
|
6 | 7 | 86% | 4.3 |
| 13 |
|
6 | 9 | 67% | 6.07 |
| 14 |
|
5 | 6 | 83% | 32.7 |
| 15 |
|
6 | 9 | 67% | 19.42 |
| 16 |
|
4 | 4 | 100% | 81.77 |
| 17 |
|
5 | 7 | 71% | 112.62 |
| 18 |
|
5 | 8 | 63% | 128.62 |
| 19 |
|
5 | 9 | 56% | 43.57 |
| 20 |
|
4 | 6 | 67% | 134.42 |
| 21 |
|
3 | 4 | 75% | 41.63 |
| 22 |
|
4 | 7 | 57% | 1.73 |
| 23 |
|
4 | 8 | 50% | 0.28 |
| 24 |
|
4 | 8 | 50% | 0.27 |
| 25 |
|
3 | 5 | 60% | 133.37 |
| 26 |
|
4 | 9 | 44% | 0.27 |
| 27 |
|
4 | 9 | 44% | 31.75 |
| 28 |
|
4 | 9 | 44% | 31.08 |
| 29 |
|
4 | 9 | 44% | 2.07 |
| 30 |
|
4 | 9 | 44% | 13.3 |
| 31 |
|
1 | 3 | 33% | 14.82 |
| 32 |
|
1 | 3 | 33% | 99.75 |
| 33 |
|
0 | 0 | 0% | 10.32 |
| 34 |
|
0 | 0 | 0% | 35.78 |
| 35 |
|
0 | 0 | 0% | 0.47 |
| 36 |
|
1 | 2 | 50% | 28.65 |
| 37 |
|
0 | 0 | 0% | 0.5 |
| 38 |
|
4 | 7 | 57% | 101.9 |
| 39 |
|
0 | 0 | 0% | 0.07 |
| 40 |
|
8 | 12 | 67% | 26.1 |
| 41 |
|
0 | 0 | 0% | 56.08 |
| 42 |
|
8 | 12 | 67% | 67.27 |
| 43 |
|
0 | 0 | 0% | 54.43 |
| 44 |
|
0 | 1 | 0% | 9.87 |
| 45 |
|
0 | 1 | 0% | 2.43 |
| 46 |
|
0 | 1 | 0% | 0.17 |
| 47 |
|
0 | 1 | 0% | 0.22 |
| 48 |
|
2 | 8 | 25% | 0.87 |
| 49 |
|
0 | 2 | 0% | 15.97 |
| 50 |
|
2 | 9 | 22% | 0.6 |
| 51 |
|
2 | 9 | 22% | 1.03 |
| 52 |
|
2 | 9 | 22% | 0.33 |
| 53 |
|
1 | 8 | 13% | 17.53 |