Đề thi Đại học môn Toán khối B năm 2010
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 458
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = 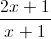 . 1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho 2. Tìm m để đường thẳng y = -2x + m cắt đồ thị (C) tại hai điểm A, B sao cho tam giác OAB có diện tích bằng √3 (O là gốc tọa độ)
. 1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho 2. Tìm m để đường thẳng y = -2x + m cắt đồ thị (C) tại hai điểm A, B sao cho tam giác OAB có diện tích bằng √3 (O là gốc tọa độ)
Câu 2: Giải phương trình: (sin2x + cos2x)cosx + 2cos2x - sinx = 0
Câu 3: Giải phương trình: 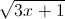 -
- 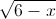 + 3x2 – 14x – 8 = 0 (x ∈
+ 3x2 – 14x – 8 = 0 (x ∈ 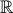 )
)
Câu 4: Tính tích phân: I = 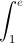
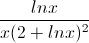 dx
dx
Câu 5: Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a, góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 600 . Gọi G là trọng tâm của tam giác A’BC. Tính thể tích khối lăng trụ đã cho và tính bán kính mặt cầu ngoại tiếp tứ diện GABC theo a
Câu 6: Cho các số thực không âm a, b, c thỏa mãn: a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức: M = 3(a2b2 + b2c2 + c2a2) + 3(ab + bc + ca) + 2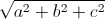
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A, có đỉnh C(-4 ; 1), phân giác trong góc A có phương trình x + y -5 = 0. Viết phương trình đường thẳng BC, biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương.
Câu 8: Trong không gian tọa độ Oxyz, cho các điểm A(1 ; 0 ; 0), B(0 ; b ; 0), C(0 ; 0 ; c), trong đó b , c dương và mặt phẳng (P): y - z + 1 = 0. Xác định b và c, biết mặt phẳng (ABC) vuông góc với mặt phẳng (P) và khoảng cách từ điểm O đến mặt phẳng (ABC) bằng 
Câu 9: Trong mặt phẳng với hệ tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn: |z - i| = |(1 + i)z|
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(2 ; √3) và elip (E): 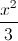 +
+ 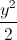 = 1. Gọi F1 và F2 là các tiêu điểm của (E) (F1có hoành độ âm); M là giao điểm có tung độ dương của đường thẳng AF1 với (E); N là điểm đối xứng của F2 qua M. Viết phương trình đường tròn ngoại tiếp tam giác ANF2.
= 1. Gọi F1 và F2 là các tiêu điểm của (E) (F1có hoành độ âm); M là giao điểm có tung độ dương của đường thẳng AF1 với (E); N là điểm đối xứng của F2 qua M. Viết phương trình đường tròn ngoại tiếp tam giác ANF2.
Câu 11: Trong không gian tọa độ Oxyz cho đường thẳng ∆: 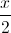 =
= 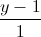 =
= 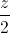 . Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM
. Xác định tọa độ của điểm M trên trục hoành sao cho khoảng cách từ M đến ∆ bằng OM
Câu 12: Giải hệ phương trình: 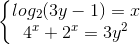 (x , y ∈
(x , y ∈ 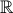 )
)
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
4 | 5 | 80% | 117.05 |
| 2 |
|
3 | 4 | 75% | 0.62 |
| 3 |
|
4 | 9 | 44% | 0.25 |
| 4 |
|
2 | 3 | 67% | 64.57 |
| 5 |
|
2 | 4 | 50% | 5.22 |
| 6 |
|
0 | 0 | 0% | 37.42 |
| 7 |
|
0 | 0 | 0% | 0.35 |
| 8 |
|
4 | 8 | 50% | 17.52 |
| 9 |
|
3 | 12 | 25% | 0.9 |
| 10 |
|
0 | 1 | 0% | 8.23 |
| 11 |
|
2 | 8 | 25% | 0.23 |