Đề thi Đại học môn Toán khối B năm 2011

Đề thi Đại học môn Toán khối B năm 2011

Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 510

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Giải phương trình: sin2xcosx + sinxcosx = cos2x + sinx + cosx (1)

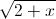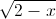Câu 2: Giải phương trình: 3 $\sqrt{2+x}$ - 6 $\sqrt{2-x}$ + 4 $\sqrt{4-x^{2}}$ = 10 - 3x (x ∈ R) (1)

Câu 3: Tính tích phân: I = 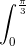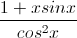$\int_{0}^{\frac{\pi }{3}}$ $\frac{1+xsinx}{cos^{2}x}$ dx

Câu 4: Cho lăng trụ ABCD.A₁B₁C₁D₁ có đáy ABCD là hình chữ nhật. AB = a, AD = a√3. Hình chiếu vuông góc của điểm A₁ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Góc giữa hai mặt phẳng (ADD₁A₁) và (ABCD) bằng 60⁰. Tính thể tích khối lăng trụ đã cho và khoảng cách từ điểm B₁ đến mặt phẳng (A₁BD) theo a.

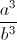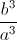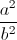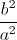Câu 5: Cho a và b là các số thực dương thỏa mãn 2(a² + b²) + ab = (a + b)(ab + 2). Tìm giá trị nhỏ nhất của biểu thức: P = 4( $\frac{a^{3}}{b^{3}}$ + $\frac{b^{3}}{a^{3}}$ ) - 9( $\frac{a^{2}}{b^{2}}$ + $\frac{b^{2}}{a^{2}}$ )

Câu 6: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆: x - y - 4 = 0; d: 2x - y - 2 = 0 Tìm tọa độ điểm N thuộc đường thẳng d sao cho đường thẳng ON cắt đường thẳng ∆ tại điểm M thỏa mãn OM.ON = 8

Câu 7: Trong không gian hệ tọa độ Oxyz, cho đường thẳng ∆: 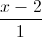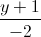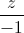$\frac{x-2}{1}$ = $\frac{y+1}{-2}$ = $\frac{z}{-1}$ và mặt phẳng (P): x + y + z - 3 = 0. Gọi I là giao điểm của ∆ và (P). Tìm tọa độ điểm M thuộc (P) sao cho MI vuông góc với ∆ và MI = 4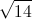 $\sqrt{14}$

Câu 8: Tìm số phức z, biết: 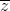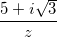$\small \overline{z}$ - $\small \frac{5+i\sqrt{3}}{z}$ - 1 = 0

Câu 9: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B( $\small \frac{1}{2}$ ; 1). Đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB tương ứng tại các điểm D, E, F. Cho D(3 ; 1) và đường thẳng EF có phương trình y - 3 = 0. Tìm tọa độ đỉnh A, biết A có tung độ dương

Câu 10: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆: 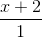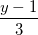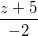$\small \frac{x+2}{1}$ = $\small \frac{y-1}{3}$ = $\small \frac{z+5}{-2}$ và hai điểm A(-2 ; 1 ; 1); B(-3 ; -1 ; 2). Tìm tọa độ điểm M thuộc đường thẳng ∆ sao cho tam giác MAB có diện tích bằng 3√5

Câu 11: Tìm phần thực và phần ảo của số phức z = (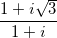 $\small \frac{1+i\sqrt{3}}{1+i}$ )³

Bạn có đủ giỏi để vượt qua

Nguyễn Thế Duy

Xếp hạng

Thành viên

Đúng

Làm

Đạt

Phút

1	Nguyễn Thế Duy	8	9	89%	3
2	mr la	6	6	100%	15.37
3	laikimoanh	4	4	100%	104.12
4	Tuy Nguyen	2	2	100%	17.28
5	Nguyễn Văn Hòa	4	9	44%	28.55
6	Tien Dinh Duc Dinh	2	3	67%	104.2
7	Nguyễn Duy Anh	1	1	100%	2.85
8	thao	1	2	50%	23.53
9	Bớt'ss Sủa's Giùm'ss	3	10	30%	4.72
10	Tuan Nguyen	5	11	45%	1.17
11	hoang nhu y	0	0	0%	2.15
12	thidaihoc	0	0	0%	0.17
13	Mai hồng bảo quyên	3	11	27%	0.5

Cùng tham gia trao đổi với bạn bè!

Lớp 12