Đề thi thử Đại học môn Toán đề số 24

Câu 1: Cho hàm số y = x⁴ – 3x² – 2. (1). Khảo sát sự biến thiên và vẽ đồ thị hàm số (2). Tìm số thực dương a để đường thẳng y = a cắt (C) tại hai điểm A, B sao cho tam giác OAB vuông tại gốc tọa độ O.

Câu 2: Giải phương trình: 3(cos³ x – sin³ x) = (4 + sin2x)cosx

Câu 3: Giải hệ phương trình: 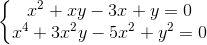 (x , y ∈ )

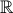Câu 4: Tính diện tích hình phẳng giới hạn bởi các đường 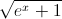y = , y = 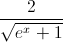 và x = ln3

Câu 5: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a√3, AD = a. Cạnh bên SC tạo với đáy một góc α thỏa mãn cosα  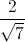= . Gọi M, N lần lượt là trung điểm của SD và SB. Biết rằng hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Tính thể tích khối chóp C. AMN và khoảng cách giữa hai đường thẳng AM và BD

Câu 6: Cho các số dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức P =  -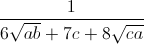 

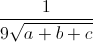
Câu 7: Trong mặt phẳng với hệ trục Oxy, cho hình chữ nhật ABCD có đường chéo AC: x + 2y - 9 = 0. Điểm M(0 ; 4) nằm cạnh BC. Xác định tọa độ của các đỉnh hình chữ nhật đã cho biết rằng diện tích của hình chữ nhật đó bằng 6, đường thẳng CD đi qua N(2 ; 8) và đỉnh C có tung độ là một số nguyên.

Câu 8: Trong không gian với hệ tọa độ Oxyz, cho các điểm A(3 ; 1 ; 1), B(0 ; 1 ; 4), C(-1 ; -3 ; 1) và mặt phẳng (α): x + y - 2z + 4 = 0. Viết phương trình mặt cầu (S) có tâm nằm trên mặt phẳng (α) và đi qua ba điểm A, B, C.

Câu 9: Trong mặt phẳng tọa độ, giả sử điểm A biểu diễn nghiệm z₁ của phương trình z² - 6z + 45 = 0 và điểm B biểu diễn số phức z₂ = -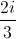z₁ . Chứng minh rằng tam giác OAB vuông

Câu 10: Trong mặt phẳng với hệ trục Oxy, cho hình chữ nhật ABCD. Hai điểm B và C thuộc trục tung. Phương trình đường chéo AC: 3x + 4y - 16 = 0. Xác định tọa độ các đỉnh của hình chữ nhật đã cho biết rằng bán kính đường tròn nội tiếp tam giác ACD bằng 1

Câu 11: Trong không gian với hệ tọa độ Oxyz, cho A(1 ; -1 ; 1), mặt phẳng (P): 2x + y - 2z + 2 = 0, đường thẳng d: 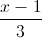 =  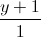= 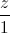. Lập phương trình mặt cầu (S) có tâm nằm trên đường thẳng d, có bán kính nhỏ nhất, tiếp xúc với mặt phẳng (P) và đi qua điểm A