Đề thi thử đại học môn Toán lần I năm 2012 - trường THPT chuyên Hà Nội Amsterdam
Thời gian thi : 180 phút - Số câu hỏi : 10 câu - Số lượt thi : 314
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y=x3-3x2+3mx+1-m có đồ thị (Cm) 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m=0 (học sinh tự giải) 2. Tìm các giác trị của tham số m để hàm số có cực trị, đồng thời đường thẳng đi qua hai điểm cực trị tạo với đường thẳng ∆: 3x+y-8=0 một góc 45o.
Câu 2: Giải phương trình: sin(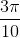 -
-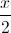 )=
)=  sin(
sin(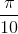 +
+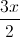 )
)
Câu 3: Tìm các giá trị của m để phương trình x2+ =m có nghiệm trên R
=m có nghiệm trên R
Câu 4: Tính tích phân: I=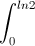
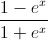 dx
dx
Câu 5: Trong mặt phẳng Oxy cho tam giác ABC vuông cân tại A. Biết rằng cạnh huyền nằm trên đường thẳng d: x+7y-31=0, điểm N(1; ) thuộc đường thẳng AC, điểm M(2;-3) thuộc đường thẳng AB. Xác định tọa độ các đỉnh của tam giác ABC.
) thuộc đường thẳng AC, điểm M(2;-3) thuộc đường thẳng AB. Xác định tọa độ các đỉnh của tam giác ABC.
Câu 6: Trong không gian tọa độ Oxyz cho hình lăng trụ đứng tam giác ABC.A’B’C’ với A(0;-3;0), B(4;0;0), C(0;3;0), B’(4;0;4). Gọi M là trung điểm của A’B’. Mặt phẳng (P) đi qua hai điểm A,M và song song với BC’, (P) cắt A’C’ tại N. Tính độ dài MN
Câu 7: Tìm số phức z thỏa mãn 2 điều kiện |z+1-2i|=|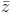 +3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo
+3+4i| và \(w = \frac{{z - 2i}}{{\overline z + i}}\) là một số thuần ảo
Câu 8: Trong mặt phẳng hệ tọa độ Oxy cho đường tròn (C): x2+y2-2x+4y+2=0. Gọi (C’) là đường tròn có tâm I'(5;1) và cắt đường tròn (C) tại 2 điểm M,N sao cho MN=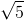 . Hãy viết phương trình của (C’)
. Hãy viết phương trình của (C’)
Câu 9: Giải hệ phương trình: 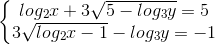
Câu 10: Cho các số dương x,y,z thỏa mãn: x(x-1)+y(y-1)+z(z-1)≤ Tìm các giá trị nhỏ nhất của: A=
Tìm các giá trị nhỏ nhất của: A=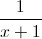 +
+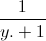 +
+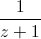 dấu "=" xảy ra khi:
dấu "=" xảy ra khi: