Đề thi thử ĐH môn Toán lần thứ IV năm 2012 - Trường THPT Đào Duy Từ
Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 355
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x3 – 3mx2 + (m2 + 2m – 3)x + 4 1.Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với m = 1. Gọi là đồ thị (C ). 2.Viết phương trình Parabol đi qua điểm cực đại, điểm cực tiểu của đồ thị ( C ) và tiếp xúc đường thẳng y = - 2x + 2.
Câu 2: Giải phương trình:
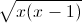 +
+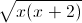 =2√x2
=2√x2
Câu 3: Giải phương trình: (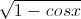 + √cosx )cos2x =
+ √cosx )cos2x =  sin4x
sin4x
Câu 4: Tính tích phân: I = 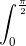
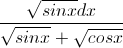
Câu 5: Cho hình chóp SABC đáy ABC là tam giác cân AB = AC, góc BAC = 2α. Hai mặt bên SAB, SAC cùng vuông góc với đáy. Cạnh bên SB = m hợp với đáy góc β. 1.Gọi H là trung điểm cạnh BC. Chứng minh SA2 + AH2 + HB2 = SB2 2.Tính thể tích của khối chóp.
Câu 6: Tìm m để hệ bất phương trình sau có nghiệm: 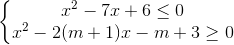
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn ( C ): x2 + y2 – 2x – 2my + m2 – 24 = 0 có tâm I và đường thẳng ∆ : mx + 4y = 0 . Tìm m biết đường thẳng ∆ cắt đường tròn ( C ) tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB bằng 12.
Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d1 : 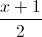 =
= 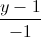 =
= 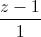 ; d2 :
; d2 : 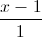 =
= 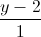 =
= 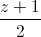 và mặt phẳng (P) : x – y – 2z + 3 = 0. Viết phương trình chính tắc của đường thẳng ∆, biết ∆ nằm trên mặt phẳng ( P ) và ∆ cắt hai đường thẳng d1, d2.
và mặt phẳng (P) : x – y – 2z + 3 = 0. Viết phương trình chính tắc của đường thẳng ∆, biết ∆ nằm trên mặt phẳng ( P ) và ∆ cắt hai đường thẳng d1, d2.
Câu 9: Cho x, y ∈ R và x > 1, y > 1. Tìm giá trị nhỏ nhất của biểu thức p = 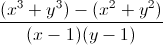
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trình cạnh AB: x – y – 2 = 0, phương trình cạnh AC: x + 2y – 5 = 0. Biết trọng tâm của tam giác G(3;2). Viết phương trình cạnh BC.
Câu 11: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆: 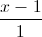 =
= 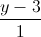 =
= 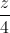 và điểm M(0; -2; 0). Viết phương trình mặt phẳng (P) đi qua điểm M song song với đường thẳng ∆ đồng thời khoảng cách giữa đường thẳng ∆ và mặt phẳng (P) bằng 4.
và điểm M(0; -2; 0). Viết phương trình mặt phẳng (P) đi qua điểm M song song với đường thẳng ∆ đồng thời khoảng cách giữa đường thẳng ∆ và mặt phẳng (P) bằng 4.