Đề thi thử vào lớp 10 môn Toán đề số 4

Thời gian thi : 120 phút - Số câu hỏi : 10 câu - Số lượt thi : 684

Click vào đề thi   Tải đề

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

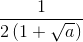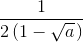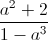
Cho biểu thức: \frac{1}{2\left ( 1+\sqrt{a}^{} \right )} + \frac{1}{2\left ( 1-\sqrt{a}^{} \right )} - \frac{a^{2}+2}{1-a^{3}}

Câu 1: Rút gọn P.

Câu 2: Tìm giá trị nhỏ nhất của P.

Giải các phương trình, hệ phương trình sau:

Câu 3: Giải phương trình:  x4 – 15x2 -100 = 0

Câu 4: Giải hệ phương trình : 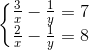\left\{\begin{matrix} \frac{3}{x}-\frac{1}{y}=7 \\\frac{2}{x}-\frac{1}{y}=8 \end{matrix}\right.

Cho hai hàm số  y= 2x2 có đồ thị (P) và y= x+3 có đồ thị d.

Câu 5: Vẽ các đồ thị (P) và d trên cùng một mặt phẳng tọa độ Oxy.

Câu 6: Gọi A là giao điểm của 2 đò thị (P) và d có hnhf độ âm. Viết phương trình đường thẳng (∆) cắt trục tung tại C, cắt trục hoành tại D. Đường thẳng d cắt trục hoành tại B. Tính tỉ số diện tích của ∆ABC và ∆ABD. 

Cho đường tròn tâm O; bàn kính R và đường tròn tâm O', bán kính R'(R>R') cắt nhau tại hai điểm A và B. Đường thẳng AB cắt  B. Vẽ tiếp tuyến chung MN của 2 đường tròn. Đường thẳng AB cắt MN tại I(B nằm giữa A và I).

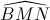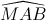
Câu 7: Chứng minh rằng: \widehat{BMN} = \widehat{MAB}

Câu 8: Chứng minh rằng: IN2 = IA.IB

Câu 9: Đường thẳng MA cắt cắt đường thẳng NB tại Q, đường thẳng NA cắt đường thẳng MB tại P. Chứng minh rằng MN//QP.

Câu 10: Cho các số thực a,b,c,d. Chứng minh rằng: 

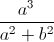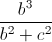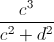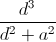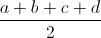
\frac{a^{3}}{a^{2}+b^{2}} + \frac{b^{3}}{b^{2}+c^{2}}+\frac{c^{3}}{c^{2}+d^{2}}+\frac{d^{3}}{d^{2}+a^{2}}≥ \frac{a+b+c+d}{2}

Bạn có đủ giỏi để vượt qua

kannaa kanna
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 kanna 8 10 80% 8.23
2 tran the minh 4 10 40% 0.63
3 Bảo Ngọc (san san) 5 9 56% 5.45
4 GIAP QUANG MINH 0 1 0% 12.33
5 Hồ Thị Hoàng Anh 6 9 67% 10.45
6 Ngô Thế Tấn 0 1 0% 2.05
7 Cao Văn Minh 2 10 20% 6.1
8 vu lac hoan 4 10 40% 4.77
9 Pham Trung Dong 0 1 0% 0.72
10 vo tan ngan 2 10 20% 0.28
11 camuyen 2 10 20% 0.22
12 Nguyễn Đăng Quý 2 10 20% 1.13

Cùng tham gia trao đổi với bạn bè!

Lớp 9