Căn bậc hai - Căn bậc ba
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 1:
Giải phương trình: 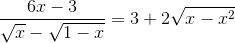
Câu hỏi số 2:
Chứng minh bất đẳng thức sau:
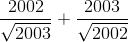 >
> 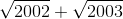
(Trích đề thi tuyển sinh THPT tỉnh Thái Bình, năm 2002 - 2003)
Câu hỏi số 3:
Chứng minh rằng: 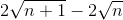 <
< 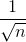 <
< 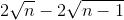 . Từ đó suy ra: 2004 < 1 +
. Từ đó suy ra: 2004 < 1 + 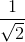 +
+ 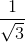 + ..... +
+ ..... + 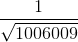 < 2005
< 2005
Câu hỏi số 4:
Với a, b là các số thực thỏa mãn đẳng thức (1 + a)(1 + b) =  , hãy tìm giá trị nhỏ nhất của biểu thức
, hãy tìm giá trị nhỏ nhất của biểu thức 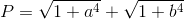
Câu hỏi số 5:
Tìm tất cả các cặp số (x;y) thỏa mãn điều kiện:
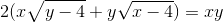
Câu hỏi số 6:
Giải phương trình:
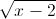 +
+ 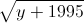 +
+ 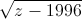 =
=  (x + y + z )
(x + y + z )
Câu hỏi số 7:
Chứng minh rằng 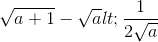 , với a>0.
, với a>0.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









