Góc với đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 21:
Cho tam giác cân ABC (AB = AC). Gọi I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp góc A, O là trung điểm đoạn IK.
Câu hỏi số 1:
Chứng minh ba điểm A, I, K thẳng hàng.
Câu hỏi số 2:
Chứng minh bốn điểm B, I, C, K cùng thuộc một đường tròn tâm O.
Câu hỏi số 3:
Chứng minh AC là tiếp tuyến của đường tròn (O)
Câu hỏi số 4:
Tính bán kính của đường tròn (O) biết AB = AC = 20 cm; BC = 24 cm
Bài 22:
Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B (O và O' thuộc hai nửa mặt phẳng bờ AB). Các đường thẳng AO và AO' cắt đường tròn (O) lần lượt ở C và D, cắt đường tròn (O') lần lượt ở E và F.
Câu hỏi số 1:
Chứng minh ba điểm B, F ,C thẳng hàng.
Câu hỏi số 2:
Chứng minh tứ giác CDEF nội tiếp được một đường tròn.
Câu hỏi số 3:
Chứng minh A là tâm đường tròn nội tiếp tam giác BDE
Câu hỏi số 4:
Tìm điều kiện để DE là tiếp tuyến chung của hai đường tròn (O) và (O')
Bài 23:
Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, M là một điểm trên cung nhỏ AC. Tiếp tuyến của đường tròn (O) tại M cắt tia DS tại S. Gọi I là giao điểm của CD và MB.
Câu hỏi số 1:
Chứng minh tứ giác AMIO nội tiếp được một đường tròn.
Câu hỏi số 2:
Chứng minh 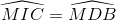 và
và 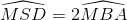
Câu hỏi số 3:
Chứng minh IM.IB = IC.ID và SM2 = SC.SD
Câu hỏi số 4:
Gọi K là trung điểm của MB. Khi M chuyển động trên cung nhỏ AC thì K chuyển động trên đường nào ?
Câu hỏi số 5:
Xác định vị trí điểm M trên cung nhỏ AC sao cho MA =  MB
MB
Bài 24:
Cho đường tròn (O; R), hai đường kính AB và CD vuông góc với nhau. Trong đoạn AB lấy điểm M khác O. Đường thẳng CM cắt đường tròn (O) tại điểm thứ hai N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến với đường tròn (O) tại N ở điểm P. Chứng minh:
Câu hỏi số 1:
Tứ giác OMNP nội tiếp được đường tròn.
Câu hỏi số 2:
Tứ giác CMPO là hình bình hành.
Câu hỏi số 3:
Tích CM.CN không đổi.
Câu hỏi số 4:
Khi M chuyển động trên đoạn AB thì P chạy trên một đoạn thẳng cố định.
Bài 25:
Cho hai đường tròn (O) và (O') bán kính R và R' (R > R') tiếp xúc ngoài tại điểm C. Gọi AC, BC là hai đường kính của đường tròn (O); (O'); DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của đoạn AB. Gọi giao điểm thứ hai của đường tròn DC với đường tròn (O') là F.
Câu hỏi số 1:
Tứ giác AEBD là hình gì?
Câu hỏi số 2:
Chứng minh ba điểm B, E, F thẳng hàng.
Câu hỏi số 3:
Chứng minh bốn điểm M, D, B, F thuộc một đường tròn.
Câu hỏi số 4:
BD cắt đường tròn (O') ở G. Chứng minh ba đường thẳng DF, EG và AB đồng quy.
Câu hỏi số 5:
Chứng minh 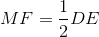 và MF là tiếp tuyến của đường tròn (O').
và MF là tiếp tuyến của đường tròn (O').
Bài 26:
Cho hai đường tròn (O); (O') cắt nhau tại hai điểm A, B. Các đường thẳng AO, AO' cắt đường tròn (O) lần lượt tại các điểm thứ hai C, D và cắt đường tròn (O') lần lượt tại các điểm thứ hai E, F.
Câu hỏi số 1:
Chứng minh rằng B, F, C thẳng hàng.
Câu hỏi số 2:
Chứng minh: tứ giác CDEF nội tiếp được.
Câu hỏi số 3:
Chứng minh rằng A là tâm đường tròn nội tiếp tam giác BDE.
Câu hỏi số 4:
Tìm điều kiện để DE là tiếp tuyến chung của các đường tròn (O), (O')
Bài 27:
Cho tam giác ABC (![]() < 90° )nội tiếp đường tròn (O; R). Vẽ các đường cao BD, CE,. Các tia BD, CE lần lượt cắt đường tròn (O; R) tại các điểm thứ hai D', E'.
< 90° )nội tiếp đường tròn (O; R). Vẽ các đường cao BD, CE,. Các tia BD, CE lần lượt cắt đường tròn (O; R) tại các điểm thứ hai D', E'.
Câu hỏi số 1:
Chứng minh rằng bốn điểm B, E, D, C nằm trên một đường tròn.
Câu hỏi số 2:
Chứng minh E'D' // ED.
Câu hỏi số 3:
Chứng minh rằng OA ┴ ED
Câu hỏi số 4:
Bây giờ cho điểm A di động trên cung lớn BC của đường tròn (O; R). Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AED không đổi.
Bài 28:
Cho đường tròn (O; R), đường kính AB và một điểm M nằm trên đường tròn sao cho MA > MB. Các tiếp tuyến của đường tròn tại M và B cắt nhau tại điểm P. Các đường thẳng AB, MP cắt nhau tại điểm Q; các đường thẳng AM, OM cắt đường thẳng BP lần lượt tại các điểm R, S.
Câu hỏi số 1:
Chứng minh rằng tứ giác AMPO là hình thang.
Câu hỏi số 2:
Chứng minh rằng MB // SQ
Câu hỏi số 3:
Gọi R1 là điểm đối xứng với R qua đường thẳng AB. Chứng minh rằng tứ giác ASQR1 nội tiếp được
Câu hỏi số 4:
Gọi giao điểm của các đường thẳng AM và SQ là R'. Cho biết tứ giác OMR'P là hình bình hành. Tính OS theo R.
Bài 29:
Một điểm M nằm trên nửa đường tròn tâm (O), đường kính AB. Gọi các điểm chính giữa của các cung AM, MB lần lượt là H, I và giao điểm của các dây AM, HI là K.
Câu hỏi số 1:
Chứng minh rằng góc HKM có độ lớn không đổi.
Câu hỏi số 2:
Vẽ đường cao IP của tam giác IAM. Chứng minh đường thẳng IP tiếp xúc với đường tròn (O; 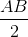 )
)
Câu hỏi số 3:
Gọi Q là trung điểm của dây MB, dựng hình bình hành APQR. Tìm tập hợp điểm R.
Câu hỏi số 4:
Trên nửa mặt phẳng bờ AB chứa điểm M. Hãy dựng một đường tròn có đường kính bằng 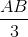 sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).
sao cho nó không có điểm chung với đường thẳng HI với mọi vị trí của điểm M trên nửa đường tròn (O).
Bài 30:
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Các tiếp tuyến tại A của các đường tròn (O) và (O') cắt đường tròn (O') và(O) theo thứ tự tại C và D. Gọi P và Q lần lượt là trung điểm của các dây cung AD và AC.
Câu hỏi số 1:
Chứng minh hai tam giác ABD và ABC đồng dạng.
Câu hỏi số 2:
Chứng minh 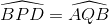
Câu hỏi số 3:
Chứng minh tứ giác APBQ nội tiếp.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









