Hàm số và các bài toán liên quan
Chuyên đề này giúp học sinh giải các bài tập về hàm số và các bài toán liên quan.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 31:
Cho hàm số y = 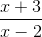 , có đồ thị (C).
, có đồ thị (C).
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
b. Tìm các giá trị m (m ∈ R) để đường thẳng d: y = -x + m cắt (C) tại hai điểm phân biệt A, B nằm ở hai phía của trục tung sao cho góc AOB nhọn (O là gốc tọa độ).
Câu hỏi số 32:
Cho hàm số y = x3 − 3mx2 + 4m3 có đồ thị (Cm)
1, Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
2, Tìm m để (Cm) có các điểm cực đại, cực tiểu ở về một phía đối với đường thẳng 3x − 2y + 8 = 0 .
Câu hỏi số 33:
Cho hàm số y = x3 - 3mx2 + (3m2 – 3)x + m2 + 1 (1), với m là tham số.
1. Khảo sát và vẽ đồ thị (C) của hàm số (1) khi m= 1 (HS tự làm ).
2. Định m để đồ thị hàm số (1) có hai đểm cực trị cách đều trục Ox.
Câu hỏi số 34:
Cho hàm số: y = 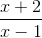 (1)
(1)
a. Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) (HS tự làm).
b. Chứng minh rằng đường thẳng y = -x + 2 là một trục đối cứng của đồ thị hàm số (1).
Câu hỏi số 35:
Cho hàm số y = x3 + (1 - 2m)x2 + (2 - m)x + m + 2 (1) m là tham số.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 2 (HS tự làm).
2. Tìm m đề đồ thị hàm số (1) có cực đại, cực tiểu và hoành độ cực tiểu bé hơn 1.
Câu hỏi số 36:
Cho hàm số y = 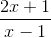 có đồ thị (H)
có đồ thị (H)
a. Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số. (HS tự làm).
b. Xác định tọa độ điểm M ∈ (H) có hoành độ dương sao cho tiếp tuyến tại M cắt 2 đường tiệm cận của tại A, B sao cho bán kính đường tròn ngoại tiếp ∆IAB = 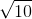 (I là giao của hai đường tiệm cận).
(I là giao của hai đường tiệm cận).
Câu hỏi số 37:
Cho hàm số y = 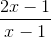 .
.
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
2. Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến cắt các trục Ox, Oy lần lượt tại các điểm phân biệt A, B sao cho OA = 4OB.
Câu hỏi số 38:
Cho hàm số: y = x3 – 3x2 + 2 có đồ thị (C)
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) (HS tự làm).
2. Viết phương trình tiếp tuyến của (C) cắt các trục Ox, Oy lần lượt tại các điểm phân biệt A, B sao cho OB = 9OA, trong đó điểm A có hoành dộ dương, điểm B có tung độ âm.
Câu hỏi số 39:
Cho hàm số: y = 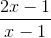
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm m để đường thẳng d: y =  x + m cắt đồ thị (C) tại hai điểm A, B sao cho KA = KB với K(2; 0).
x + m cắt đồ thị (C) tại hai điểm A, B sao cho KA = KB với K(2; 0).
Câu hỏi số 40:
Cho hàm số y = x4 - 2(m + 1)x2 + 2m + 1 (Cm), điểm K(3; -2)
1. Khảo sát và vẽ đồ thị hàm số khi m = 0 (HS tự làm).
2. Tìm m để (Cm) cắt trục hoành tại 4 điểm A, B, C, D phân biệt sao cho diện tích tam giác KAC bằng 4. (các điểm A, B, C, D được sắp xếp theo thứ tự hoành độ tăng dần).
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









