Hàm số và các bài toán liên quan
Chuyên đề này giúp học sinh giải các bài tập về hàm số và các bài toán liên quan.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 1:
Cho hàm số y = x3 −6x2 +3(m+ 2)x+ 4m−5 có đồ thị (Cm), với m là tham số thực.
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho khi m =1.
b) Tìm m để trên (Cm) tồn tại đúng hai điểm có hoành độ lớn hơn 1 sao cho các tiếp tuyến tại mỗi điểm đó của (Cm) vuông góc với đường thẳng d : x + 2y +3 = 0.
Câu hỏi số 2:
Cho hàm số y = f (x) =−x3 +3mx −2 với m là tham số thực.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1.
2. Tìm các giá trị của m để bất phương trình f (x) ≤−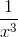 
đúng với mọi x ≥1.
Câu hỏi số 3:
Cho hàm số y = x4 - 2x2 - 3
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (HS tự làm).
2. Tìm m để đường thẳng d: y = m cắt đồ thị (C) tại 4 điểm phân biệt M, N, P, Q (sắp thứ tự từ trái sang phải) sao cho độ dài các đoạn thẳng MN, NP, PQ là độ dài 3 cạnh của một tam giác vuông.
Câu hỏi số 4:
Cho hàm số y = 
x3 – mx2 + 6(m - 1)x + 
(1) có đồ thị (Cm)
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1. (HS tự làm)
b. Tìm m để trên (Cm) có hai điểm phân biệt M (x1; y1) và N(x2; y2) sao cho tiếp tuyến tại mỗi điểm đó vuông góc với đường thẳng x + 3y - 6 = 0 và √x1 + √x2 ≤ 2√3
Câu hỏi số 5:
Cho hàm số y =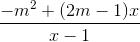 
(1) (m là tham số)
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) ứng với m = 0 (HS tự làm).
2. Chứng minh rằng với mọi giá trị của m khác 1 đồ thị hàm số (1) luôn tiếp xúc với đường thẳng y = x.
Câu hỏi số 6:
Cho hàm số y = -x3 + 3x - 1
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
b. Xác định m (m ∈ R) để đường thẳng d: y = mx - 2m - 3 cắt (C) tại 3 điểm phân biệt trong đó có đúng một điểm có hoành độ âm.
Câu hỏi số 7:
Cho hàm số y = x3 - 3x2 + 2
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
2. Tìm m để đường thẳng (∆): y = (2m - 1)x - 4m cắt đồ thị (C) tại đúng hai điểm M, N phân biệt và M, N cùng với điểm P(-1; 6) tạo thành tam giác MNP nhận gốc tọa độ làm trọng tâm.
Câu hỏi số 8:
Cho hàm số y =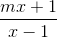 
có đồ thị (C)
1/ Khảo sát và vẽ đồ thị của hàm số khi m = 1.(HS tự làm)
2/ Viết phương trình tiếp tuyến d với (C) tại điểm có hoành độ x = 2, tìm m để khoảng cách từ điểm A(3; 5) tới tiếp tuyến d là lớn nhất.
Câu hỏi số 9:
Cho hàm số y=x3 + 3x2 -2
a.Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b.Tìm trên đường thẳng y= 9x - 7 những điểm mà qua đó kẻ được ba tiếp tuyến đến đồ thị (C) của hàm số.
Câu hỏi số 10:
Cho hàm số: y =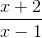 
có đồ thị (C)
Khảo sát và vẽ đồ thị hàm số (C) (HS Tự vẽ)
Viết phương trình 2 đường thẳng d1, d2 đi qua giao điểm I của hai tiệm cận và cắt đồ thị (C) tại 4 điểm phân biệt là các đỉnh của 1 hình chữ nhật biết đường chéo của hình chữ nhật đó có độ dài bằng √30
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
