Hệ thức lượng trong tam giác vuông
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 41:
Tính giá trị của các biểu thức sau:
a. A = +
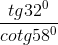 - 2(sin200.cos700 + cos200.sin700)
- 2(sin200.cos700 + cos200.sin700)
b. B = +
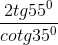
Câu hỏi số 42:
Cho tam giác vuông ABC (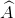 = 900, AB ≠ AC). Chứng minh:
= 900, AB ≠ AC). Chứng minh:
a. 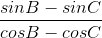 < 0
< 0
b. 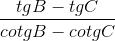 < 0
< 0
Câu hỏi số 43:
Cho ∆ABC có hai đường trung tuyến BM và CN vuông góc với nhau, các góc 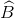 và
và 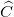 đều là góc nhọn. Chứng minh: cotgB + cotgC ≥
đều là góc nhọn. Chứng minh: cotgB + cotgC ≥ 
Câu hỏi số 44:
Cho tam giác vuông ABC (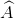 = 900). Chứng minh rằng cotgB + cotgC ≥ 2
= 900). Chứng minh rằng cotgB + cotgC ≥ 2
Câu hỏi số 45:
Cho tam giác vuông ABC (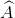 = 900), AB = 7,5 cm, AC = 10 cm, trung tuyến AM. Tính các tỉ số lượng giác của
= 900), AB = 7,5 cm, AC = 10 cm, trung tuyến AM. Tính các tỉ số lượng giác của 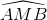 .
.
Câu hỏi số 46:
Cho ∆ABC có AB = 4,5 cm, AC = 6 cm, AC = 6 cm, BC = 7,5 cm. Kẻ đường phân giác BD của 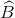 cắt AC tại D. Tính các tỉ số lượng giác của
cắt AC tại D. Tính các tỉ số lượng giác của 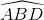
Câu hỏi số 47:
Cho ∆ABC, đường cao AH và trung tuyến AM. Biết AH = 12 cm, HB = 9 cm. HC = 16 cm. Tính các tỉ số lượng giác của 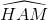 .
.
Câu hỏi số 48:
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, vẽ tia Ax và vẽ tia By ⊥ AB. Gọi O là trung điểm của đoạn thẳng AB và C là 1 điểm thuộc tia Ax. Vẽ tia Cz sao cho 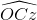 =
= 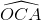 , tia Cz cắt By tại D (AC < BD). Hai đường thẳng AB và CD cắt nhau tại E.
, tia Cz cắt By tại D (AC < BD). Hai đường thẳng AB và CD cắt nhau tại E.
a. Kẻ OH ⊥ CD. Chứng minh OC2.HD = OD2.HC
b. Kẻ HK ⊥ AB. Chứng minh 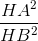 =
= 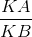 =
= 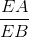
Câu hỏi số 49:
Cho tam giác vuông ABC (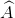 = 900). Kẻ AH ⊥ BC. Chu vi ∆ABH = 9 cm và chu vi ∆ACH = 12 cm.
= 900). Kẻ AH ⊥ BC. Chu vi ∆ABH = 9 cm và chu vi ∆ACH = 12 cm.
Tính chu vi và diện tích tam giác ABC.
Câu hỏi số 50:
Cho hình thang ABCD (AB // CD, AB < CD), M và N là trung điểm của hai đáy AB và CD, biết MN =  (CD - AB)
(CD - AB)
a. Chứng minh 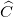 +
+ 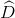 = 900.
= 900.
b. Biết AD = AB = 6 cm, BC = 8 cm. Tính diện tích hình thang ABCD.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









