Hệ thức lượng trong tam giác vuông
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 61:
Không dùng bảng và máy tính bỏ túi, hãy sắp xếp giá trị các tỉ số lượng giác sau đây theo thứ tự nhỏ đến lớn :
sin 20°, cos 20°, sin 55°, cos 40°, tg 70°.
Câu hỏi số 62:
Cho tam giác ABC vuông tại A có đường cao AH = 6 cm. Hãy tính các cạnh của tam giác đó, biết CH = 8 cm
Câu hỏi số 63:
Cho hình vuông ABCD. Lấy điểm E trên cạnh BC. Tia AE cắt đường thẳng CD tại G. Trên nửa mặt phẳng bờ là đường thẳng AE chứa tia AD, kẻ AF ⊥ AE và AF = AE.
a. Chứng minh 3 điểm F, D, C thẳng hàng.
b. Chứng minh 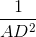 =
= 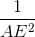 +
+ 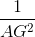
c. Biết AD = 13 cm, AF : AG = 10 : 13. Tính độ dài của FG.
Câu hỏi số 64:
Cho tam giác vuông ABC (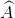 = 900), đường cao AH. Biết AB : AC = 1 : √3; HC - HB = 8 cm.
= 900), đường cao AH. Biết AB : AC = 1 : √3; HC - HB = 8 cm.
a. Tính các cạnh của ∆ABC.
b. Hình chữ nhật MNPQ nội tiếp ∆ABC (các điểm P và Q thuộc cạnh BC; M thuộc cạnh AB và N thuộc cạnh AC). Tìm GTLN của diện tích hình chữ nhật MNPQ.
Câu hỏi số 65:
Cho tam giác ABC (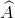 = 900), đường cao AH, đường phân giác AD. Biết AH = 24 cm, HC - HB = 14 cm. Tính BD và DA.
= 900), đường cao AH, đường phân giác AD. Biết AH = 24 cm, HC - HB = 14 cm. Tính BD và DA.
Câu hỏi số 66:
Cho hình thang vuông ABCD (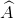 =
= 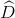 = 900), đường chéo BD vuông góc với cạnh bên BC. Biết AD = 12cm, DC = 25cm. Tinh độ dài các cạnh AB, BC và đường chéo DB.
= 900), đường chéo BD vuông góc với cạnh bên BC. Biết AD = 12cm, DC = 25cm. Tinh độ dài các cạnh AB, BC và đường chéo DB.
Câu hỏi số 67:
Cho đoạn thẳng AB = 13cm. Vẽ nửa đường tròn tâm O, đường kính AB. Từ điểm C trên nửa đường tròn, kẻ CD ⊥ AB. Biết CD = 6 cm. Tính AD và BD.
Câu hỏi số 68:
Cho tam giác vuông ABC (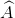 = 900), đường cao AH = 6 cm. Tỉ số hai cạnh góc vuông AB : AC = 3 : 7. Tính BH và HC.
= 900), đường cao AH = 6 cm. Tỉ số hai cạnh góc vuông AB : AC = 3 : 7. Tính BH và HC.
Câu hỏi số 69:
Cho tam giác vuông ABC (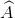 = 900), đường cao AH. Biết AB : AC = 3 : 4 và BC = 15cm. Tính BH và HC.
= 900), đường cao AH. Biết AB : AC = 3 : 4 và BC = 15cm. Tính BH và HC.
Câu hỏi số 70:
Mọi điểm trên mặt phẳng được đánh dấu bởi một trong hai dấu (+) và (-). Chứng minh rằng luôn chỉ ra 3 điểm trên mặt phẳng làm thành tam giác vuông cân mà 3 đỉnh của nó được đánh cùng dấu.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









