Hình học không gian
Hình học không gian nghiên cứu về điểm, đường thẳng... Chuyên đề này giúp học sinh giải quyết các bài toán điển hình về giải hình không gian bằng tọa
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 1:
Cho hình chóp đều S. ABCD có độ dài cạnh đáy bằng a , mặt bên của hình chóp tạo với mặt đáy góc 60o. Mặt phẳng (P ) chứa AB và đi qua trọng tâm tam giác SAC cắt SC, SD lần lượt tại M, N . Tính thể tích khối chóp S. ABMN theo a .
Câu hỏi số 2:
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật với SA vuông góc với đáy, G là trọng tâm tam giác SAC, mặt phẳng (ABG) cắt SC tại M, cắt SD tại N. Tính thể tích của khối đa diện MNABCD biết SA=AB=a và góc hợp bởi đường thẳng AN và mp(ABCD) bằng 300.
Câu hỏi số 3:
Cho hình chóp S.ABCD có đáy là hình bình hành với AB = 2a, BC = a√2, BD = a√6. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trong tâm G của tam giác BCD. Biết SG = 2a. Tính thể tích của khối chóp S.ABCD và khoảng cách từ điểm A đến mặt phẳng (SBD) theo a.
Câu hỏi số 4:
Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuông góc của A trên SC. Chứng minh SC ⊥ (ABH). Tính thế tích khối chóp S.ABH theo a.
Câu hỏi số 5:
Cho tam giác đều ABC cạnh a và tam giác cân SAB đỉnh S không cùng nằm trong một mặt phẳng. Gọi H, K lần lượt là trung điểm của AB, AC, biết góc giữa 2 mặt phẳng (SAB) và (ABC) là 600, SA = 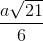 , SC < HC. Tính thể tích khối chóp S.ABC và khoảng cách giữa HK và mp (SBC) theo a.
, SC < HC. Tính thể tích khối chóp S.ABC và khoảng cách giữa HK và mp (SBC) theo a.
Câu hỏi số 6:
Cho hình chóp S.ABCD có đáy là ABCD là hình vuông cạnh a, tam gíac SAB đều, tam giác SCD vuông cân tại S. Gọi I, J, K lần lượt là trung điểm các cạnh AB, CD, SA. Chứng minh rằng (SIJ) ⊥ (ABCD). Tính thể tích khối chóp K.IBCD.
Câu hỏi số 7:
Cho hình chóp S.ABCD có ABCD là hình chữ nhật với AB = 2a; BC = a√2. Mặt phẳng (SAB) vuông góc với mặt đáy (ABCD) và SA = a√3, SB = a. Gọi K là trung điểm của CB. Hãy tính thể tích khối chóp S.ABCD và tính khoảng cách giữa hai đường chéo nhau SC và DK.
Câu hỏi số 8:
Cho hình lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông tại C. M là trung điểm A'C'. Biết AC = a, BC = a√3, mặt phẳng (ABC') hợp với mặt phẳng (ABC) góc 600. Tính thể tích khối lăng trụ ABC.A'B'C' và khoảng cách AM và BC' theo a .
Câu hỏi số 9:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a. Góc giữa mặt bên và mặt đáy bằng 600. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SD và BC. Tính thể tích khối tứ diện AMNP theo a.
Câu hỏi số 10:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Có SA = AB = a√3 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60o.
1. Tính thể tích khối chóp S.ABC.
2. Trong tam giác SAC vẽ phân giác góc A cắt cạnh SC tại D. Tính khoảng cách giữa hai đường thẳng AC và BD.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









