Số phức
Việc mở rộng trường số phức để giải những bài toán mà không thể giải trong trường số thực. Số phức được sử dụng trong nhiều lĩnh vực khoa học,
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 1:
Tìm số phức z thoả mãn │1-iz│ = │ 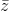 -3i│ và z -
-3i│ và z -  là số thuần ảo.
là số thuần ảo.
Câu hỏi số 2:
Gọi z1, z2 là hai nghiệm phức của phương trình z2 – (3+i)z +4 =0. Viết dạng lượng giác của các số phức z12014, z22014
Câu hỏi số 3:
Giải phương trình sau trên trường số phức C : | z | - iz = 1 – 2i.
Câu hỏi số 4:
Tìm tất cả các số phức z, biết |z - 1 - 2i|2+zi + 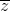 =11 + 2i
=11 + 2i
Câu hỏi số 5:
Cho số phức z thoả mãn: z - 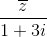 =
= 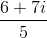 . Tìm phần thực của số phức z2013.
. Tìm phần thực của số phức z2013.
Câu hỏi số 6:
Tìm số phức z thỏa mãn 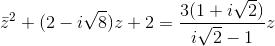
Câu hỏi số 7:
Giải phương trình sau trên tập số phức C: z4 – 2z3 – z2 - 2z + 1 = 0
Câu hỏi số 8:
Hãy tính tổng các số phức z thỏa mãn điều kiện z2 = │z│2 – 3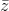
Câu hỏi số 9:
Gọi z1, z2 là 2 nghiệm của phương trình z2 - (2cos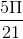 )z + 1 = 0. Tìm số n nguyên dương nhỏ nhất sao cho z1n + z2n = 1.
)z + 1 = 0. Tìm số n nguyên dương nhỏ nhất sao cho z1n + z2n = 1.
Câu hỏi số 10:
Tìm modun của số phức w = b + ci (b, c ∈ R), biết số phức 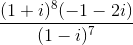 là nghiệm của phương trình z2 + bz + c = 0
là nghiệm của phương trình z2 + bz + c = 0
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









