Tổ hợp - Xác suất
Chuyên đề này giới thiệu cho các bạn một số dạng bài tập về công thức tổ hợp, xác suất.
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài tập luyện
Câu hỏi số 11:
Có hai hộp A và B đựng các cây viết. Hộp a gồm 5 cây viết màu đỏ và 6 cây viết màu xanh. Hộp B gồm 7 cây viết màu đỏ và 8 cây viết màu xanh. Lấy ngẫu nhiên cung một lúc từ mỗi hộp ra một cây viết. Tính xác suất sao cho hai cây viết được lấy ra có cùng màu.
Câu hỏi số 12:
Một hộp có 5 viên bi đỏ ,3 viên bi vàng và 4 viên bi xanh .Hỏi có bao nhiêu cách lấy ra 4 viên bi trong đó số bi đỏ lớn hơn số bi vàng
Câu hỏi số 13:
Tìm hệ số của x9trong khai triển: (1-√3x)2n; nϵ N*, biết 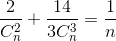
Câu hỏi số 14:
Tìm hệ số của x20 trong khai triển Newton của biểu thức (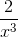 + x5)n biết rằng:
+ x5)n biết rằng:
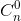 -
- 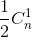 +
+ 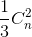 - .... + (-1)n
- .... + (-1)n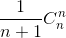 =
= 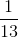 .
.
Câu hỏi số 15:
Trong một lớp gồm có 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Tìm xác suất để 4 học sinh được gọi có cả nam và nữ.
Câu hỏi số 16:
Tìm hệ số của x3 trong khai triển Niuton của biểu thức (2 + 2x – x2 – x3 )n
biết rằng: 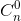 -
- 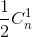 +
+ 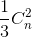 - ... +
- ... + 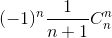 =
= 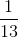
Câu hỏi số 17:
Chứng minh rằng với mọi n nguyên dương ta có:
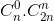 +
+ 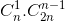 +
+ 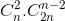 + ... +
+ ... + 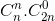 =
= 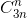
Câu hỏi số 18:
Với n là số nguyên dương, chứng minh:
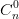 + 2
+ 2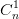 + 3
+ 3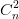 + ...+ (n + 1)
+ ...+ (n + 1)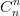 = (n + 2)2n-1
= (n + 2)2n-1
Câu hỏi số 19:
Tìm hệ số chứa x4 trong khai triển (1 + 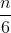 x + 3x2)n- 2biết
x + 3x2)n- 2biết
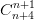 -
- 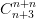 = 7(n + 3).
= 7(n + 3).
Câu hỏi số 20:
Chứng minh rằng :
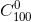 -
- 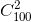 +
+ 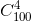 -
- 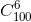 + ..... -
+ ..... - 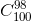 +
+ 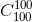 = -250
= -250
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









