Khi sử dụng các thiết bị nhiệt và thủy tinh trong phòng thí nghiệm Vật lí chúng ta cần lưu ý điều gì?
Đáp án đúng là: C
Sử dụng lý thuyết an toàn trong phòng thực hành
Đáp án cần chọn là: C
Lĩnh vực nghiên cứu nào sau đây là của Vật lí?
Đáp án đúng là: C
Sử dụng lý thuyết các lĩnh vực nghiên cứu của Vật lí
Đáp án cần chọn là: C
Biển báo hình bên cho biết ý nghĩa gì?

Đáp án đúng là: B
Sử dụng lý thuyết biển cảnh báo
Đáp án cần chọn là: B
Gọi \(\overrightarrow d \) là độ dịch chuyển và \(\overrightarrow v \) là vận tốc trung bình của một chất điểm trong khoảng thời gian t thì
Đáp án đúng là: A
Vận tốc trung bình: \(\overrightarrow v = \dfrac{{\overrightarrow d }}{t}\)
Đáp án cần chọn là: A
Độ dịch chuyển của một vật là
Đáp án đúng là: B
Sử dụng lý thuyết về độ dịch chuyển của một vật.
Đáp án cần chọn là: B
Một vật ném ngang từ độ cao h với vận tốc đầu \({v_0}\). Bỏ qua lực cản của không khí. Tầm xa của vật là
Đáp án đúng là: C
Sử dụng kiến thức về chuyển động ném ngang.
Đáp án cần chọn là: C
Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là:
Đáp án đúng là: D
Lý thuyết về chuyển động biến đổi đều.
Đáp án cần chọn là: D
Chọn đáp án đúng biểu diễn biểu thức gia tốc?
Đáp án đúng là: A
Biểu thức gia tốc: \(\overrightarrow a = \dfrac{{\Delta \overrightarrow v }}{{\Delta t}}\)
Đáp án cần chọn là: A
Sự rơi tự do là
Đáp án đúng là: A
Lý thuyết về sự rơi tự do.
Đáp án cần chọn là: A
Quỹ đạo chuyển động của một vật bị ném xiên là:
Đáp án đúng là: C
Sử dụng lý thuyết chuyển động ném xiên
Đáp án cần chọn là: C
Ngoài lực của động cơ, thời gian tăng tốc của ô tô phụ thuộc vào nhiều yếu tố khác như điều kiện mặt đường thử nghiệm, khối lượng xe, điều kiện thời tiết, lốp xe, độ cao so với mực nước biển, vv… Mẫu xe điện có thời gian tăng tốc nhanh nhất được thử nghiệm đã tăng tốc từ 0 km/h đến 97,0 km/h trong 1,98 giây. Gia tốc của xe trong thời gian đó là:
Đáp án đúng là: C
Gia tốc: \(a = \dfrac{{v - {v_0}}}{t}\)
Đáp án cần chọn là: C
Một vật rơi tự do không vận tốc ban đầu từ độ cao 5m xuống. Lấy \(g = 10{\rm{m/}}{{\rm{s}}^2}\) Vận tốc của nó ngay trước khi chạm đất là
Đáp án đúng là: D
Sử dụng kiến thức về sự rơi tự do.
Đáp án cần chọn là: D
Một vật chuyển động thẳng chậm dần đều với vận tốc đầu là 10 m/s, sau 2s vật có vận tốc là 8 m/s. Vật dừng lại sau thời gian
Đáp án đúng là: D
Sử dụng kiến thức về chuyển động thẳng chậm dần đều.
Đáp án cần chọn là: D
Một xe ô tô đang chuyển động đều thì hãm phanh chuyển động thẳng chậm dần đều. Chọn chiều dương là chiều chuyển động, nhận xét nào dưới đây là đúng?
Đáp án đúng là: C
Đặc điểm của chuyển động chậm dần đều: a.v < 0
Đáp án cần chọn là: C
Khi nào độ lớn vận tốc trung bình và tốc độ trung bình của một chất điểm chuyển động là như nhau?
Đáp án đúng là: B
Vận tốc trung bình: \(\overrightarrow {{\upsilon _{tb}}} = \dfrac{{\overrightarrow d }}{t}\)
Tốc độ trung bình: \({v_{tb}} = \dfrac{s}{t}\)
Độ lớn của độ dịch chuyển bằng quãng đường khi vật không đổi chiều chuyển động
Đáp án cần chọn là: B
Một vật được ném từ độ cao h = 45 m với vận tốc đầu \({v_0} = 20\,\,m/s\) theo phương nằm ngang, bỏ qua sức cản của không khí, lấy \(g = 10\,\,m/{s^2}\). Tầm ném xa của vật là
Đáp án đúng là: B
Tầm xa của vật bị ném ngang: \(L = {v_0}\sqrt {\dfrac{{2H}}{g}} \)
Đáp án cần chọn là: B
Xét quãng đường AB dài 500 m với A là vị trí nhà em và B là vị trí tiệm tạp hóa. Chọn A là gốc tọa độ và chiều dương hướng từ A đến B. Độ dịch chuyển và quãng đường em đi được khi đi từ nhà đến tiệm tạp hóa rồi quay trở về nhà lần lượt là:
Đáp án đúng là: D
Sử dụng lý thuyết độ dịch chuyển và quãng đường
Đáp án cần chọn là: D
Một vật chuyển động có đồ thị vận tốc – thời gian như hình vẽ.
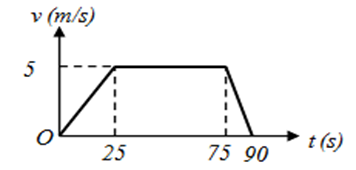
Xác định độ dịch chuyển của vật trong thời gian 75s.
Đáp án đúng là: D
Độ dịch chuyển trong chuyển động thẳng biến đổi đều: \(d = {v_0}t + \dfrac{{a{t^2}}}{2}\)
Độ dịch chuyển trong chuyển động thẳng đều: \(d = vt\)
Đáp án cần chọn là: D
Trong các đặc điểm sau đây của quãng đường và độ dịch chuyển của một vật chuyển động, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Quãng đường có phương và chiều xác định. | ||
| b) Quãng đường không thể có độ lớn bằng 0. | ||
| c) Độ dịch chuyển có thể có độ lớn bằng 0. | ||
| d) Độ dịch chuyển chỉ có đơn vị là mét. |
Đáp án đúng là: S; Đ; Đ; S
Độ dịch chuyển là một đại lượng vecto, quãng đường là đại lượng vô hướng
Đáp án cần chọn là: S; Đ; Đ; S
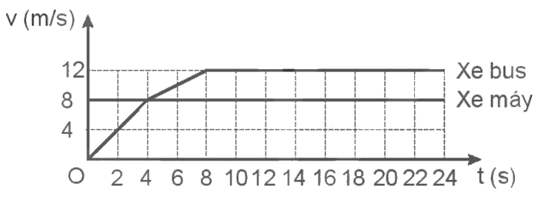
Hình vẽ dưới đây biểu diễn đồ thị vận tốc – thời gian của một xe bus và một xe máy chạy cùng chiều trên một đường thẳng. Xe bus đang đứng yên, bắt đầu chuyển động thì xe máy đi tới.
| Đúng | Sai | |
|---|---|---|
| a) Xe máy chuyển động nhanh dần đều. | ||
| b) Xe bus bắt đầu chạy nhanh hơn xe máy tại thời điểm 4 s. | ||
| c) Xe bus đuổi kịp xe máy tại thời điểm 4 s. | ||
| d) Khi xe bus đuổi kịp xe máy, xe máy đã đi được quãng đường 42 m. |
Đáp án đúng là: S; Đ; S; S
Sử dụng kĩ năng đọc đồ thị vận tốc – thời gian
Độ dịch chuyển của chuyển động biến đổi đều: \(d = {v_0}t + \dfrac{1}{2}a{t^2}\)
Độ dịch chuyển của chuyển động đều: d = vt
Xe bus đuổi kịp xe máy khi độ dịch chuyển của hai xe bằng nhau
Đáp án cần chọn là: S; Đ; S; S
Thả rơi tự do một vật khối lượng 2 kg từ độ cao 180 m xuống mặt đất. Lấy \(g = 10\,\,m/{s^2}\).
| Đúng | Sai | |
|---|---|---|
| a) Thời gian vật chuyển động là 6 giây. | ||
| b) Tốc độ của vật khi chạm đất là 60 m/s. | ||
| c) Quãng đường vật rơi được trong giây thứ 3 là 45 m. | ||
| d) Quãng đường vật rơi được trong giây cuối cùng là 125 m. |
Đáp án đúng là: Đ; Đ; S; S
Quãng đường đi được của vật rơi tự do: \(s = \dfrac{1}{2}g{t^2}\)
Tốc độ của vật rơi tự do: v = gt
Đáp án cần chọn là: Đ; Đ; S; S
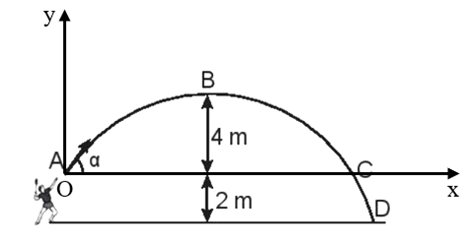
Hình bên vẽ quỹ đạo của một quả cầu lông được đánh lên với vận tốc ban đầu \({v_0} = 10\,\,m/s\) ở độ cao 2 m so với mặt đất. Bỏ qua sức cản của không khí và lấy \(g = 9,8\,\,m/{s^2}\).
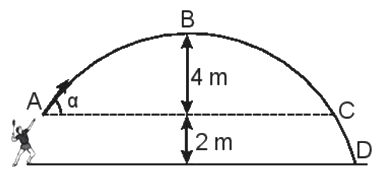
| Đúng | Sai | |
|---|---|---|
| a) Độ lớn của góc \(\alpha = {62^0}\). | ||
| b) Tốc độ của quả cầu ở vị trí B là 6,8 m/s. | ||
| c) Khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của người đánh cầu là 9,4 m. | ||
| d) Tốc độ của quả cầu tại vị trí D là 14,2 m/s. |
Đáp án đúng là: Đ; S; Đ; S
Tầm bay cao của chuyển động ném xiên: \(H = \dfrac{{{v_0}^2{{\sin }^2}\alpha }}{{2g}}\)
Vận tốc theo phương ngang: \({v_x} = {v_0}\cos \alpha \)
Vận tốc theo phương thẳng đứng: \({v_y} = {v_0}\sin \alpha - gt\)
Tốc độ của vật bị ném xiên: \(v = \sqrt {{v_x}^2 + {v_y}^2} \)
Tầm bay cao của chuyển động ném xiên: \(H = \dfrac{{{v_0}^2{{\sin }^2}\alpha }}{{2g}}\)
Chuyển động ném xiên theo phương Ox: \(x = \left( {{v_0}\cos \alpha } \right).t\)
Theo phương Oy: \(\left\{ \begin{array}{l}{v_y} = {v_0}\sin \alpha - gt\\y = \left( {{v_0}\sin \alpha } \right)t - \dfrac{{g{t^2}}}{2}\end{array} \right.\)
Đáp án cần chọn là: Đ; S; Đ; S
Một học sinh dùng đồng hồ bấm giây để đo chu kì dao động điều hòa của một con lắc lò xo. Sau 5 lần đo, xác định được khoảng thời gian T của mỗi dao động toàn phần như sau:

Giá trị trung bình của chu kì con lắc là bao nhiêu giây? (Kết quả làm tròn đến 2 chữ số thập phân).
Đáp án đúng là:
Giá trị trung bình: \(\overline A = \dfrac{{{A_1} + {A_2} + ... + {A_n}}}{n}\)
Đáp án cần điền là: 2,11
Một người đi bộ từ nhà đến bến xe bus cách nhà 1 km về phía Tây. Đến bến xe, người đó lên xe bus đi tiếp 5 km về phía Nam. Quãng đường người đó đi được trong cả chuyến đi là bao nhiêu km?
Đáp án đúng là:
Tổng quãng đường: \(s = {s_1} + {s_2}\)
Đáp án cần điền là: 6
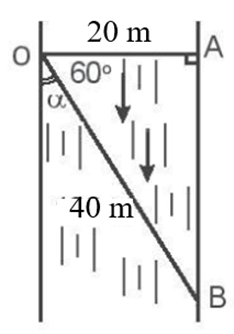
Một người bơi từ bờ này sang bờ kia của một con sông rộng 20 m theo hướng vuông góc với bờ sông. Do nước sông chảy mạnh nên quãng đường người đó bơi gấp 2 lần so với khi nước lặng. Vị trí điểm tới cách điểm đối diện với điểm khởi hành của người bơi là bao nhiêu mét? (Kết quả làm tròn đến một chữ số thập phân).
Đáp án đúng là:
Độ dịch chuyển: \(\overrightarrow d = \overrightarrow {{d_1}} + \overrightarrow {{d_2}} \)
Định lí Pi-ta-go: \(AB = \sqrt {O{B^2} - O{A^2}} \)
Đáp án cần điền là: 34,6
Một vật chuyển động thẳng đều với tốc độ 5 m/s. Thời gian để vật chuyển động hết quãng đường 0,5 km là bao nhiêu giây?
Đáp án đúng là:
Thời gian chuyển động: \(t = \dfrac{S}{v}\)
Đáp án cần điền là: 100
Một electron chuyển động trong ống đèn hình của một máy thu hình. Nó tăng tốc đều đặn từ vận tốc \({3.10^4}\,\,m/s\) đến vận tốc \({5.10^6}\,\,m/s\) trên một đoạn đường thẳng bằng 2 cm. Hãy tính thời gian electron đi hết quãng đường đó. (Đơn vị: ns, kết quả làm tròn đến hàng đơn vị).
Đáp án đúng là:
Độ dịch chuyển trong chuyển động biến đổi đều: \(d = \dfrac{{{v^2} - {v_0}^2}}{{2a}}\)
\(a = \dfrac{{v - {v_0}}}{t}\)
Đáp án cần điền là: 8
Trong khoảng thời gian liên tiếp bằng nhau 4 s, chất điểm chuyển động thẳng nhanh dần đều đi được những quãng đường lần lượt là 24 m và 64 m. Tính gia tốc của chất điểm. (Đơn vị: \(m/{s^2}\)).
Đáp án đúng là:
Quãng đường trong chuyển động thẳng biến đổi đều: \(s = {v_0}t + \dfrac{1}{2}a{t^2}\)
Mối liên hệ giữa quãng đường, tốc độ, gia tốc: \({v^2} - {v_0}^2 = 2as\)
Đáp án cần điền là: 2,5