
Biển báo nào dưới đây cảnh báo khu vực có điện thế cao?
Đáp án đúng là: A
Kiến thức về các loại biển báo.
Đáp án cần chọn là: A
Đơn vị nào sau đây là đơn vị của nhiệt nóng chảy riêng của vật rắn?
Đáp án đúng là: D
Lý thuyết về nhiệt nóng chảy riêng.
Đáp án cần chọn là: D
Trong xilanh của một động cơ có chứa một lượng khí ở nhiệt độ \({47^0}C\) và áp suất 0,7 atm. Sau khi bị nén thể tích của khí giảm đi 5 lần và áp suất tăng lên tới 8 atm. Tính nhiệt độ của khí ở cuối quá trình nén?
Đáp án đúng là: D
Áp dụng phương trình khí lý tưởng: \(\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\)
Đáp án cần chọn là: D
Trong đàn ghi-ta điện, pickup là một thiết bị cảm biến âm thanh được lắp đặt trên cây đàn guitar, giúp chuyển đổi các dao động của dây đàn thành tín hiệu điện. Tín hiệu này sau đó được truyền đến ampli hoặc hệ thống âm thanh để phát ra âm thanh từ đàn guitar. Giả sử rằng một cuộn dây của bộ thu có 500 vòng và diện tích mỗi vòng là \(0,005{m^2}\). Khi dây đàn dao động, từ trường biến thiên với tần số 440 Hz và cảm ứng từ có độ lớn 0,04 T. Suất điện động cảm ứng cực đại trong cuộn dây của bộ thu khi dây đàn dao động có độ lớn bằng:

Đáp án đúng là: A
Áp dụng công thức tính suất điện động cực đại: \({E_0} = NBS\omega \)
Đáp án cần chọn là: A
Một lượng khí xác định biến đổi theo các quá trình (1) - (2) - (3) - (4) như hình vẽ. Biết nhiệt độ của chất khí ở trạng thái (1) là \({T_1} = 300K\). Nhiệt độ của chất khí này ở trạng thái (4) là
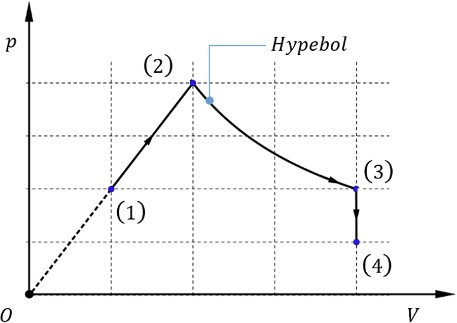
Đáp án đúng là: C
Áp dụng phương trình trạng thái khí lí tưởng: \(\dfrac{{pV}}{T} = const\)
Đáp án cần chọn là: C
Khi so sánh hạt nhân \({}_6^{12}C\) và hạt nhân \({}_6^{14}C\), phát biểu nào sau đây đúng?
Đáp án đúng là: D
Số neutron có trong hạt nhân: \(N = A - Z.\)
Đáp án cần chọn là: D
Xét một vòng dây dẫn kín (C), diện tích S được đặt trong từ trường đều cảm ứng từ \(\overrightarrow B \)tạo với véc tơ pháp tuyến \(\overrightarrow n \) của mặt phẳng vòng dây một góc α thì từ thông gửi qua diện tích vòng dây được xác định theo biểu thức:
Đáp án đúng là: A
Công thức tính từ thông qua một vòng dây là \(\phi = BSc{\rm{os}}\alpha \)
Đáp án cần chọn là: A
Nội dung nào sau đây không phải là mô hình động học phân tử về cấu tạo chất?
Đáp án đúng là: B
Lý thuyết về mô hình động học phân tử.
Đáp án cần chọn là: B
Biết nhôm có nhiệt dung riêng là 896J/kg.K và nhiệt nóng chảy riêng là \(3,{9.10^5}J\). Nhiệt lượng cần cung cấp cho miếng nhôm khối lượng 200 g ở nhiệt độ \({58^0}C\) để nó hóa lỏng hoàn toàn ở nhiệt độ \({658^0}C\) là
Đáp án đúng là: C
- Nhiệt lượng cần cung cấp để một vật tăng nhiệt độ: \(Q = mc\Delta t.\)
- Nhiệt lượng cần cung cấp để vật nóng chảy hoàn toàn ở nhiệt độ nóng chảy: \(Q = m\lambda .\)
Đáp án cần chọn là: C
Phát biểu nào sau đây là sai khi nói về các phóng xạ?
Đáp án đúng là: D
Lý thuyết về phóng xạ \({\beta ^ - }.\)
Đáp án cần chọn là: D
Một mạch kín hình vuông, cạnh 10 cm, đặt vuông góc với một từ trường đều có độ lớn thay đổi theo thời gian. Tính tốc độ biến thiên của cảm ứng từ, biết cường độ dòng điện cảm ứng 2 A và điện trở của mạch 5 Ω
Đáp án đúng là: A
Công thức tính độ lớn suất điện động cảm ứng: \(e = \left| {\dfrac{{\Delta B}}{{\Delta t}}} \right|.S\), với \(e = i.R\)
Đáp án cần chọn là: A
Một khung dây dẫn hình chữ nhật kín ABCD chuyển động song song với đoạn dây dẫn thẳng dài vô hạn mang dòng điện I chạy qua như hình vẽ. Dòng điện cảm ứng trong khung.
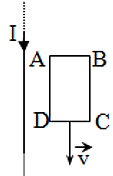
Đáp án đúng là: A
Lý thuyết về cách xác định chiều của dòng điện cảm ứng.
Đáp án cần chọn là: A
Trong quá trình hít vào, cơ hoành và cơ liên sườn của một người co lại, mở rộng khoang ngực và hạ thấp áp xuất không khí bên trong xuống dưới môi trường xung quanh để không khí đi vào qua miệng và mũi đến phổi. Giả sử phổi của một người chứa 6000 ml không khí ở áp suất 1 atm. Nếu người đó mở rộng khoang ngực thêm 500 ml bằng cách giữ mũi và miệng đóng lại để không hít không khí vào phổi thì áp suất không khí trong phổi theo atm sẽ là bao nhiêu? Giả sử nhiệt độ không khí không đổi.
Đáp án đúng là: B
Áp dụng định luật Boyle: \({P_1}{V_1} = {P_2}{V_2}\)
Đáp án cần chọn là: B
Giả thiết rằng rượu ethylic có nhiệt hoá hơi riêng là \(0,{9.10^6}J/kg\) và khối lượng riêng là 0,8 kg/l. Nhiệt lượng cần thiết để 10 lít rượu ethylic hoá hơi hoàn toàn ở nhiệt độ sôi là:
Đáp án đúng là: B
- Khối lượng của rượu: \(m = \rho V.\)
- Áp dụng công thức nhiệt lượng cần thiết để làm hóa hơi hoàn toàn chất lỏng: \(Q = mL = \rho VL\)
Đáp án cần chọn là: B
Công thức \(\dfrac{V}{T} = const\) áp dụng cho quá trình biến đổi trạng thái nào của một khối khí định?
Đáp án đúng là: B
Lý thuyết về các đẳng quá trình.
Đáp án cần chọn là: B
Chu kì bán rã của một chất phóng xạ là khoảng thời gian để
Đáp án đúng là: D
Nhớ lại khái niệm chu kì bán rã.
Đáp án cần chọn là: D
Một người được điều trị ung thư bằng phương pháp chiếu xạ gamma. Biết rằng chất phóng xạ dùng điều trị có chu kỳ bán rã là 100 ngày. Cứ 10 ngày người đó đi chiếu xạ 1 lần. Ở lần chiếu xạ đầu tiên bác sĩ đã chiếu xạ với liều lượng thời gian là 20 phút. Hỏi ở lần chiếu xạ thứ 6 người đó cần phải chiếu xạ bao lâu để vẫn nhận được nồng độ chiếu xạ như trên. (Vẫn dùng lượng chất ban đầu ở các lần chiếu xạ)
Đáp án đúng là: D
- Khối lượng chất phóng xạ sau thời gian t: \(m = {m_0}{2^{ - \dfrac{t}{T}}}\)
- Lượng chất bị mất đi sau thời gian ∆t: \(\Delta m = {m_0}\left( {1 - {2^{ - \dfrac{{\Delta t}}{T}}}} \right)\)
Đáp án cần chọn là: D
Bản chất lực tương tác giữa các nucleon trong hạt nhân là
Đáp án đúng là: D
Lý thuyết về lực hạt nhân.
Đáp án cần chọn là: D
Một nhóm học sinh lớp 12 thực hiện thí nghiệm thực hành đo nhiệt nóng chảy riêng của nước đá. Họ đã lựa chọn bộ dụng cụ thí nghiệm như hình 1 gồm: biến thế nguồn (1), bộ đo cồng suất nguồn điện có tích hợp chức năng đo thời gian (2), nhiệt kế điện tử có độ phân giải nhiệt độ ±0, 1∘C (3), nhiệt lượng kế bằng nhựa có vỏ xốp kèm dây điện trở (4), cân điện tử (5), các dây nối.

Họ cho viên nước đá có khối lượng 0,02 kg và một ít nước vào bình nhiệt lượng kế sao cho dây điện trở chìm trong hỗn hợp nước và nước đá.
Khi tiến hành đo họ khuấy liên tục nước đá, cứ sau mỗi hai phút lại ghi số đo công suất trên oát kế và nhiệt độ trên nhiệt kế. Kết quả đo được ở bảng sau:
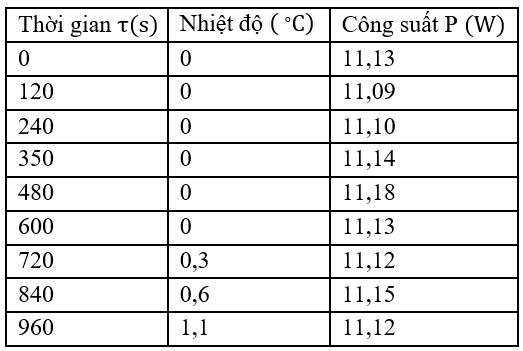
Từ bảng số liệu họ vẽ được đồ thị biểu diễn sự thay đổi nhiệt độ theo thời gian của nước trong bình nhiệt lượng kế như hình 2.
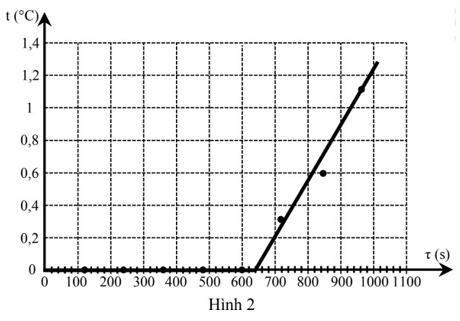
| Đúng | Sai | |
|---|---|---|
| a) Công suất trung bình của dòng điện qua điện trở trong nhiệt lượng kế là 11,13 W. | ||
| b) Với kết quả họ thu được thì nhiệt nóng chảy riêng trung bình của nước đá đo được là 3, 45.105 J/kg. |
||
| c) Khi tiến hành đo, họ khuấy liên tục nước đá để nhiệt độ của hỗn hợp nước và nước đá đồng đều. | ||
| d) Trên đồ thị vẽ được, họ tìm ra thời điểm kết thúc quá trình nóng chảy của viên nước đá nằm trong khoảng thời gian từ thời điểm 600 s đến thời điểm 700 s là không phù hợp với bảng số liệu. |
Đáp án đúng là: Đ; S; Đ; S
- Công thức tính giá trị trung bình.
- Nhiệt lượng cung cấp để nước đá tan hoàn toàn: \(Q = P.\tau = m\lambda .\)
- Phân tích số liệu từ đồ thị.
Đáp án cần chọn là: Đ; S; Đ; S
Một ngôi nhà có thể tích phần không gian bên trong là \(40\,\,{m^3}\). Vào một ngày mùa đông, nhiệt độ trong ngôi nhà vào buổi sáng sớm là \({20^0}C\) và đến giữa trưa là \({25^0}C\). Cho biết áp suất khí quyển không đổi trong ngày là 1 atm và khối lượng mol của không khí là 29 g/mol.

| Đúng | Sai | |
|---|---|---|
| a) Khối lượng không khí thoát ra khỏi căn phòng từ buổi sáng sớm đến giữa trưa là 0,81 kg. | ||
| b) Ở buổi trưa các phân tử khí trong ngôi nhà chuyển động nhanh hơn so với buổi sáng. | ||
| c) Số phân tử khí có trong ngôi nhà vào buổi sáng sớm là \(7,{51.10^{26}}\) phân tử. | ||
| d) Từ buổi sáng sớm đến giữa trưa, nhiệt độ trong ngôi nhà tăng 278 K. |
Đáp án đúng là: Đ; Đ; S; S
Phương trình Clapeyron: pV = nRT
Khối lượng khí: \(m = n\mu \)
Đáp án cần chọn là: Đ; Đ; S; S
Một khung dây hình tròn điện tích \(S = 15c{m^2}\) gồm N = 10 vòng dây, đặt trong từ trường đều cảm ứng từ \(\overrightarrow B \) hợp với mặt phẳng khung dây một góc \({60^0}\) như hình vẽ. Biết B = 0,04T, điện trở của khung dây là R = 0,2 Ω.
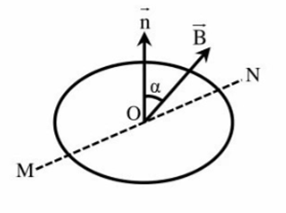
| Đúng | Sai | |
|---|---|---|
| a) Góc tạo bởi véc tơ cảm ứng từ \(\overrightarrow B \) và véc tơ pháp tuyến \(\overrightarrow n \) của mặt phẳng khung dây là \({60^0}\). | ||
| b) Từ thông gửi qua khung dây là \(5,{196.10^{ - 4}}Wb\). | ||
| c) Độ biến thiên của từ thông qua khung dây khi quay khung dây quanh đường kính MN một góc \({360^0}\) là \({6.10^{ - 4}}Wb\). |
||
| d) Cho từ trường tăng đều từ 0,04 T đến 0,1 T trong khoảng thời gian \(\Delta t = 0,05s\) thì cường độ dòng điện cảm ứng xuất hiện trong khung có cường độ 0,78 A. |
Đáp án đúng là: S; Đ; S; S
- Công thức tính từ thông: \(\Phi = NBS\cos \alpha .\)
- Suất điện động cảm ứng có độ lớn: \({e_c} = N\left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = N\left| {\dfrac{{\Delta B.S.\cos \alpha }}{{\Delta t}}} \right|\)
Đáp án cần chọn là: S; Đ; S; S
Hạt nhân \({}_{92}^{235}U\) hấp thụ một neutron nhiệt rồi vỡ ra thành hai hạt nhân \({}_{53}^{138}I\) và \({}_Z^AX\) kèm theo giải phóng 3 hạt neutron mới. Cho biết khối lượng nguyên tử của \({}_{92}^{235}U\), \({}_{53}^{138}I\), \({}_Z^AX\) lần lượt là 235,04393 u, 137,92281 u và 94,91281 u , khối lượng của hạt neutron là 1,00866 u
| Đúng | Sai | |
|---|---|---|
| a) Phản ứng này chỉ có thể xảy ra ở nhiệt độ cỡ hàng trăm triệu độ. | ||
| b) Hạt nhân \({}_Z^AX\) có 39 proton và 95 neutron. | ||
| c) Năng lượng toả ra sau phản ứng là 177,9 MeV. | ||
| d) Năng lượng ra khi 1,00 g \({}_{92}^{235}U\) phân hạch hết theo phản ứng trên là 7,29.1010J. |
Đáp án đúng là: S; S; Đ; Đ
- Lý thuyết về phản ứng phân hạch và nhiệt hạch.
- Áp dụng định luật bảo toàn số khối và điện tích tìm A và Z.
- Áp dụng công thức tính năng lượng của phản ứng hạt nhân: \(\Delta E = \left( {{m_t} - {m_s}} \right){c^2}.\)
- Năng lượng tỏa ra khi phân hạch hết m g chất X: \(E = N\Delta E = \dfrac{m}{M}.{N_A}.\Delta E\)
Đáp án cần chọn là: S; S; Đ; Đ
Một thí nghiệm khảo sát sự thay đổi nhiệt độ của một lượng rượu Etylic theo nhiệt lượng cung cấp thu được đồ thị có dạng như hình bên. Biết nhiệt dung riêng của rượu Etylic là c = 2500 J/(kgK). Nhiệt hóa hơi riêng của rượu Etylic xác định được trong thí nghiệm trên là bao nhiêu kJ/kg?
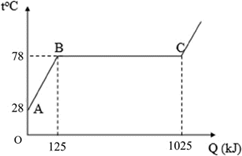
Đáp án đúng là:
- Công thức tính nhiệt lượng trong quá trình truyền nhiệt để làm thay đổi nhiệt độ: \(Q = mc\Delta t.\)
- Công thức tính nhiệt lượng trong quá trình làm nóng chảy hoàn toàn vật ở nhiệt độ nóng chảy: \(Q = L.m\)
Đáp án cần điền là: 900
Một căn phòng hở có kích thước như hình vẽ. Ban đầu không khí trong phòng ở điều kiện tiêu chuẩn (nhiệt độ ở 0°C; áp suất 1,013.105 Pa). Người ta tăng nhiệt độ không khí trong phòng lên tới 200C. Cho biết khối lượng mol của không khí bằng 29 g/mol. Khối lượng không khí đã ra khỏi phòng khi được tăng nhiệt độ là bao nhiêu kg? (Kết quả làm tròn đến phần nguyên).
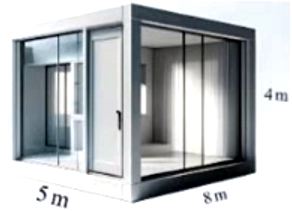
Đáp án đúng là:
Áp dụng phương trình Clapeyron: \(pV = nRT = \dfrac{m}{M}RT\)
Đáp án cần điền là: 14
Cho một lượng khí lý tưởng xác định ở điều kiện nhiệt độ không thay đổi. Nếu áp suất của lượng khí đó tăng thêm 4.105 Pa thì thể tích của lượng khí đó giảm đi 2 lít. Nếu áp suất của lượng khí đó giảm đi 105 Pa thì thể tích tăng thêm 3 lít. Thể tích ban đầu của khí nói trên là bao nhiêu lít? (làm tròn kết quả đến chữ số hàng đơn vị).
Đáp án đúng là:
+ Trong quá trình đẳng nhiệt thì áp suất tỉ lệ nghịch với thể tích.
+ Áp dụng định luật Boyle: \({p_1}{V_1} = {p_2}{V_2}\).
Đáp án cần điền là: 3
Hạt nhân nhôm \({}_{13}^{27}Al\)có khối lượng mAl = 26,9972 amu. Biết khối lượng proton và neutron lần lượt là mp = 1,0073 amu, mn = 1,0087 amu. Độ hụt khối của hạt nhân \({}_{13}^{27}Al\) là bao nhiêu amu? (làm tròn đến 2 chữ số có nghĩa).
Đáp án đúng là:
Độ hụt khối của hạt nhân \(_Z^AX\): \(\Delta m = \left[ {Z{m_p} + \left( {A - Z} \right){m_n}} \right] - {m_X}.\)
Đáp án cần điền là: 0,22
Một bệnh nhân ung thư tuyến giáp được tiêm một liều thuốc chứa 20 mg đồng vị phóng xạ \({}_{53}^{131}I\). Biết \({}_{53}^{131}I\) có chu kì bán rã là 8 ngày đêm.
Cho số Avogadro \({N_A} \approx 6,{022.10^{23}}mo{l^{ - 1}},1Ci = 3,{7.10^{10}}Bq\). Độ phóng xạ của liều thuốc trên là bao nhiêu Ci? (Kết quả làm tròn đến phần nguyên).
Đáp án đúng là:
Công thức độ phóng xạ: \({H_0} = \lambda {N_0} = \dfrac{{\ln 2}}{T}.\dfrac{{{m_0}}}{M}.{N_A}\)
Đáp án cần điền là: 2492
Một đoạn dây dẫn mang dòng điện cường độ 1,5 A đặt trong một từ trường đều thì chịu một lực từ có độ lớn 0,3 N. Nếu sau đó cường độ dòng điện tăng thêm 0,5 A thì lực từ tác dụng lên đoạn dây dẫn bằng bao nhiêu N?
Đáp án đúng là:
Công thức lực từ: \(F = BI\ell \sin \alpha .\)
Đáp án cần điền là: 0,4
