Đối với dao động tuần hoàn, số lần dao động được lặp lại trong một đơn vị thời gian gọi là
Đáp án đúng là: A
Tần số là số dao động thực hiện được trong một đơn vị thời gian.
Đáp án cần chọn là: A
Tại nơi có gia tốc trọng trường g, một con lắc đơn có sợi dây dài l đang dao động điều hòa. Tần số góc dao động của con lắc là
Đáp án đúng là: D
Sử dụng công thức tính tần số góc của con lắc đơn.
Đáp án cần chọn là: D
Khi một vật dao động điều hoà thì
Đáp án đúng là: D
Sử dụng lí thuyết dao động điều hoà.
Đáp án cần chọn là: D
Một vật dao động điều hòa với phương trình \(x = 4\cos \left( {6\pi t + \dfrac{\pi }{4}} \right)\,\,cm\). Tần số góc của vật là
Đáp án đúng là: B
Phương trình dao động: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Với x là li độ
A là biên độ
\(\omega \) là tần số góc
\(\varphi \) là pha ban đầu
\(\left( {\omega t + \varphi } \right)\) là pha dao động
Đáp án cần chọn là: B
Một chất điểm dao động điều hòa với phương trình \(x = 6\cos \left( {4\pi t + \dfrac{\pi }{2}} \right)cm\). Biên độ dao động của chất điểm là
Đáp án đúng là: D
Phương trình dao động điều hòa: \(x = A.\cos \left( {\omega t + \varphi } \right)\)
Với: x là li độ, A là biên độ dao động, \(\omega \) là tần số góc, \(\varphi \) là pha ban đầu, \(\left( {\omega t + \varphi } \right)\) là pha của dao động.
Đáp án cần chọn là: D
Dao động tắt dần được ứng dụng trong thiết bị nào sau đây?
Đáp án đúng là: D
Sử dụng lí thuyết ứng dụng của dao động tắt dần.
Đáp án cần chọn là: D
Mối liên hệ giữa tần số góc \(\omega \) và chu kì T của một dao động điều hòa là
Đáp án đúng là: A
Áp dụng công thức \(\omega = \dfrac{{2\pi }}{T}.\)
Đáp án cần chọn là: A
Bộ phận giảm xóc trong ô tô, xe máy là ứng dụng của
Đáp án đúng là: A
Sử dụng lí thuyết ứng dụng của dao động tắt dần.
Đáp án cần chọn là: A
Một con lắc đơn có chiều dài dây treo là l dao động tại một nơi trên Trái Đất với tần số 2 Hz. Nếu cắt bỏ đi một đoạn dây treo bằng \(\dfrac{3}{4}\) chiều dài ban đầu thì con lắc đơn mới dao động điều hòa với chu kỳ
Đáp án đúng là: C
Công thức tính chu kì con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Đáp án cần chọn là: C
Trong dao động cơ tắt dần, các đại lượng nào sau đây giảm dần theo thời gian?
Đáp án đúng là: D
Sử dụng định nghĩa dao động tắt dần.
Đáp án cần chọn là: D
Đồ thị li độ theo thời gian của dao động điều hòa là
Đáp án đúng là: C
Sử dụng lí thuyết dao động điều hoà.
Đáp án cần chọn là: C
Tác dụng vào hệ dao động một ngoại lực cưỡng bức tuần hoàn có biên độ không đổi nhưng tần số f thay đổi được, ứng với mỗi giá trị của f thì hệ sẽ dao động cưỡng bức với biên độ A. Hình bên là đồ thị biểu diễn sự phụ thuộc của A vào f. Chu kì dao động riêng của hệ gần nhất với giá trị nào sau đây?
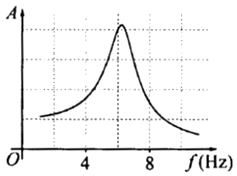
Đáp án đúng là: D
Con lắc có biên độ cực đại khi có cộng hưởng: chu kì của lực cưỡng bức bằng chu kì riêng của con lắc.
Đáp án cần chọn là: D
Gia tốc tức thời trong dao động điều hòa biến đổi
Đáp án đúng là: D
Sử dụng lí thuyết dao động điều hoà.
Đáp án cần chọn là: D
Một vật dao động điều hòa có đồ thị như hình vẽ. Phương trình dao động của vật là
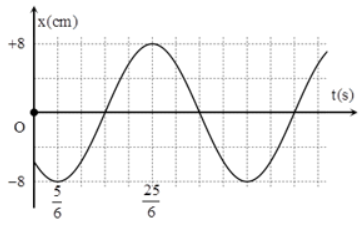
Đáp án đúng là: C
Sử dụng kĩ năng đọc đồ thị để viết phương trình dao động.
Đáp án cần chọn là: C
Chu kì con lắc đơn có chiều dài l dao động điều hoà tại vị trí có gia tốc trọng trường g được tính bởi biểu thức
Đáp án đúng là: A
Sử dụng lí thuyết dao động điều hoà.
Đáp án cần chọn là: A
Ở một nơi trên mặt đất, con lắc đơn có chiều dài l dao động điều hòa với chu kì T. Cũng tại nơi đó, con lắc đơn có chiều dài \(\dfrac{l}{4}\) dao động điều hòa với chu kì là
Đáp án đúng là: A
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \).
Đáp án cần chọn là: A
Một con lắc lò xo gồm lò xo có độ cứng 200N/m và vật có khối lượng 50g. Lấy \({\pi ^2} = 10\). Chu kì dao động của vật là
Đáp án đúng là: A
Chu kì của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \).
Đáp án cần chọn là: A
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 40 N/m dao động điều hòa trên mặt phẳng nằm ngang với biên độ 6 cm. Mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là
Đáp án đúng là: D
Cơ năng của con lắc lò xo: \({\rm{W}} = \dfrac{1}{2}k{A^2}\)
Đáp án cần chọn là: D
Một vật dao động điều hòa
| Đúng | Sai | |
|---|---|---|
| a) Biên độ là li độ cực đại của vật so với vị trí cân bằng. | ||
| b) Tần số là số dao động vật thực hiện được trong 1 giây. | ||
| c) Chu kì là thời gian vật thực hiện được 1 dao động. | ||
| d) Mối liên hệ giữa tần số góc và chu kì: \(\omega = \dfrac{T}{{2\pi }}\). |
Đáp án đúng là: Đ; Đ; Đ; S
Sử dụng lý thuyết dao động điều hòa
Đáp án cần chọn là: Đ; Đ; Đ; S
Một vật dao động điều hòa có đồ thị li độ - thời gian như hình vẽ.
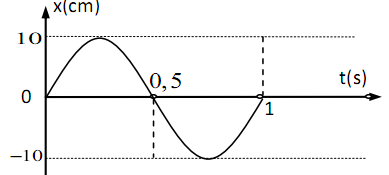
| Đúng | Sai | |
|---|---|---|
| a) Biên độ của dao động là 10 cm. | ||
| b) Chu kì của dao động là 1 s. | ||
| c) Vận tốc cực đại của vật là 20 cm/s. | ||
| d) Gia tốc cực đại của vật là \(40\pi \,\,cm/{s^2}\). |
Đáp án đúng là: Đ; Đ; S; S
Sử dụng kĩ năng đọc đồ thị
Tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
Vận tốc cực đại: \({v_{\max }} = \omega A\)
Gia tốc cực đại: \({a_{\max }} = {\omega ^2}A\)
Đáp án cần chọn là: Đ; Đ; S; S
Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo nhẹ có độ cứng 40 N/m, được treo vào một điểm cố định. Giữ vật ở vị trí lò xo dãn 10 cm rồi thả nhẹ cho vật dao dộng điều hòa theo phương thẳng đứng. Biết tốc độ cực đại của vật bằng 70 cm/s. Lấy \(g = 9,8\,\,m/{s^2}\).
| Đúng | Sai | |
|---|---|---|
| a) Tần số góc của dao động là \(14\pi \,\,rad/s\). | ||
| b) Khối lượng của vật là 0,289 kg. | ||
| c) Cơ năng của con lắc là 50 mJ. | ||
| d) Thế năng của con lắc tại vị trí lò xo không biến dạng là 50 mJ. |
Đáp án đúng là: S; S; Đ; Đ
Tốc độ cực đại của vật dao động điều hòa: \({v_{\max }} = \omega A\)
Tần số góc của con lắc lò xo: \(\omega = \sqrt {\dfrac{k}{m}} \)
Ở VTCB, lò xo dãn một đoạn: \(\Delta {l_0} = \dfrac{{mg}}{k}\)
Cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}m{\omega ^2}{A^2}\)
Đáp án cần chọn là: S; S; Đ; Đ
Một con lắc đơn có chiều dài 100 cm, khối lượng vật nhỏ 0,2 kg được treo tại nơi gia tốc rơi tự do \(g = 9,8\,\,m/{s^2}\). Con lắc dao động với biên độ 5 cm. Bỏ qua mọi ma sát.
| Đúng | Sai | |
|---|---|---|
| a) Chu kì của con lắc là 1,98 s. | ||
| b) Cơ năng của con lắc là 4,9 mJ. | ||
| c) Tại li độ 3 cm, động năng của vật là 4,4 mJ. | ||
| d) Thế năng của con lắc ở li độ 2 cm là 2,1 mJ. |
Đáp án đúng là: S; S; S; S
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Cơ năng của con lắc đơn: \(W = \dfrac{1}{2}\dfrac{{mg{A^2}}}{l}\)
Động năng của con lắc đơn: \({W_d} = \dfrac{1}{2}\dfrac{{mg\left( {{A^2} - {x^2}} \right)}}{l}\)
Thế năng của con lắc đơn: \({W_t} = \dfrac{1}{2}\dfrac{{mg{x^2}}}{l}\)
Đáp án cần chọn là: S; S; S; S
Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ vào thời gian t của một chất điểm dao động điều hòa. Chu kì dao động của chất điểm bằng bao nhiêu giây?
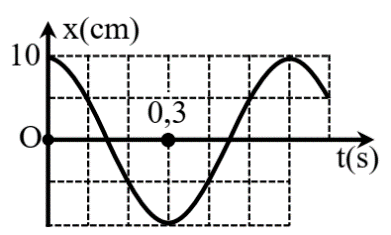
Đáp án đúng là:
Sử dụng kĩ năng đọc đồ thị
Đáp án cần điền là: 0,6
Một con lắc lò xo có quả nặng khối lượng 200 g đang dao động điều hòa với phương trình \(x = 5\cos \left( {20t + \pi } \right)\,\,\left( {cm} \right)\), t được tính bằng giây. Độ cứng của lò xo bằng bao nhiêu N/m?
Đáp án đúng là:
Áp dụng công thức \(\omega = \sqrt {\dfrac{k}{m}} \)
Đáp án cần điền là: 80
Một vật dao động điều hòa có độ lớn vận tốc cực đại là \(10\pi \,\,cm/s\). Tốc độ trung bình của vật trong một chu kì dao động là bao nhiêu cm/s?
Đáp án đúng là:
Tốc độ trung bình trong một chu kì: \({v_{tb}} = \dfrac{{4A}}{T}\)
Đáp án cần điền là: 20
Một vật nhỏ khối lượng 150 g dao động điều hòa với chu kì 0,2 s và cơ năng 90 mJ. Chọn mốc thế năng tại vị trí cân bằng. Lấy \({\pi ^2} = 10\). Tại li độ 2 cm, tỉ số động năng và thế năng của vật là bao nhiêu?
Đáp án đúng là:
Tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
Cơ năng: \(W = \dfrac{1}{2}m{\omega ^2}{A^2}\)
Thế năng: \({W_t} = \dfrac{1}{2}m{\omega ^2}{x^2}\)
Động năng: \({W_d} = W - {W_t}\)
Đáp án cần điền là: 2
Một vật nhỏ dao động điều hòa, khi vật qua vị trí có li độ \({x_1} = 0\) thì vật có tốc độ \({v_1} = 50cm/s\), khi vật qua vị trí có li độ \({x_2} = 3cm\) thì vật có tốc độ \({v_2} = 40cm/s\). Biên độ dao động của vật bằng bao nhiêu cm?
Đáp án đúng là:
Hệ thức độc lập theo thời gian: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
Đáp án cần điền là: 5
Một chất điểm dao động điều hòa trên trục Ox với biên độ 10 cm, chu kì 1 s. Thời điểm ban đầu vật qua vị trí có li độ 5 cm theo chiều dương. Kể từ thời điểm ban đầu đến khi chất điểm qua vị trí có gia tốc cực đại lần đầu tiên thì tốc độ trung bình của chất điểm là bao nhiêu cm/s?
Đáp án đúng là:
Tốc độ trung bình: \(v = \dfrac{s}{t}\)
Sử dụng VTLG
Đáp án cần điền là: 37,5