Góc lượng giác có số đo $\dfrac{5\pi}{3}$ rad thì có số đo theo đơn vị độ là
Đáp án đúng là: C
Đổi đơn vị đo: $1 \text{rad} = \left( \dfrac{180}{\pi} \right)^{{^\circ}}$
Đáp án cần chọn là: C
Phương trình \(\cos x = \dfrac{{ - 1}}{2}\) có các nghiệm là:
Đáp án đúng là: A
Giải phương trình lượng giác \(\cos x = m\).
Đáp án cần chọn là: A
Trong không gian cho hai đường thẳng \(a,\,\,b\). Có tất cả bao nhiêu vị trí tương đối giữa \(a\) và \(b\)?
Đáp án đúng là: D
Có 4 vị trí tương đối giữa hai đường thẳng trong không gian
Đáp án cần chọn là: D
Hàm số $y = \cos x$ là hàm số:
Đáp án đúng là: B
Hàm số $y = \cos x$ là hàm số có $\cos( - x) = \cos x$, $\cos(x + 2\pi) = \cos x$
Đáp án cần chọn là: B
Khẳng định nào sau đây là sai?
Đáp án đúng là: A
Kiểm tra các công thức lượng giác cơ bản:
- Công thức cộng.
- Công thức nhân đôi.
- Công thức biến đổi tổng thành tích.
Đáp án cần chọn là: A
Trong không gian cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), đường thẳng \(b\) bất kỳ nằm trong mặt phẳng \(\left( P \right)\). Có tất cả bao nhiêu vị trí tương đối giữa \(a\) và \(b\)?
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Hình chiếu song song của điểm O lên $(SAD)$ theo phương của đường thẳng SB là:
Đáp án đúng là: D
Sử dụng tính chất hình chiếu song song:
1. Xác định mặt phẳng chứa O và song song với SB.
2. Tìm giao tuyến của mặt phẳng đó với mặt phẳng (SAD).
3. Tìm điểm cắt của đường thẳng qua O song song với SB với giao tuyến vừa tìm được.
Đáp án cần chọn là: D
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Giao tuyến của hai mặt phẳng $(\text{MCD})$ và $(\text{ADN})$ là :
Đáp án đúng là: C
Muốn tìm giao tuyến của hai mặt phẳng: ta tìm hai điểm chung thuộc cả hai mặt phẳng. Nối hai điểm chung đó được giao tuyến cần tìm.
Đáp án cần chọn là: C
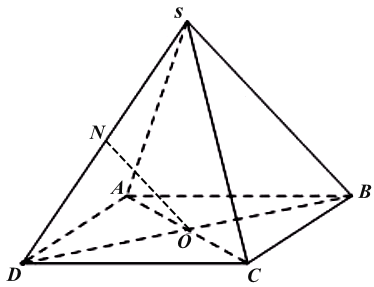
Cho hình chóp S.ABCD (tham khảo hình vẽ). Gọi O là giao điểm của AC và BD, I là giao điểm của AB và CD. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$ là
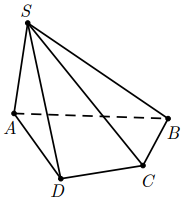
Đáp án đúng là: C
Xác định giao tuyến của hai mặt phẳng:
- Xác định điểm A thuộc cả hai mặt phẳng $(\alpha)$ và $(\beta)$.
- Tìm điểm B thứ hai cũng thuộc cả $(\alpha)$ và $(\beta)$.
Đường thẳng đi qua hai điểm A và B chính là giao tuyến của hai mặt phẳng $(\alpha)$ và $(\beta)$.
Đáp án cần chọn là: C
Hàm số $y = \tan x$ tuần hoàn với chu kì là
Đáp án đúng là: D
Chu kì tuần hoàn của hàm lượng giác.
Đáp án cần chọn là: D
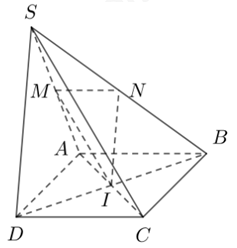
Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AB và BC (tham khảo hình vẽ). Khẳng định nào dưới đây đúng?

Đáp án đúng là: D
Tính chất của đường trung bình trong tam giác ABC.
Đáp án cần chọn là: D
Tìm tập giá trị \(T\) của hàm số \(y = 3\cos 2x + 5.\)
Đáp án đúng là: C
Sử dụng \( - 1 \le \cos 2x \le 1\).
Đáp án cần chọn là: C
Các câu sau là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Qua một điểm \(A\) nằm ngoài mặt phẳng \(\left( \beta \right)\) cho trước, có vô số mặt phẳng \(\left( \alpha \right)\) chứa \(A\) song song với \(\left( \beta \right)\) | ||
| b) Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. | ||
| c) Cho hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\) song song với nhau. Khi đó một mặt phẳng nếu cắt \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt theo các giao tuyến \(a,\,\,b\) thì \(a\) song song với \(b\) | ||
| d) Hai mặt phẳng phân biệt không cắt nhau thì song song. |
Đáp án đúng là: S; Đ; Đ; Đ
Kiểm tra tính đúng sai của mệnh đề
Đáp án cần chọn là: S; Đ; Đ; Đ
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(I\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA,\,\,SB\). Xét tính đúng, sai của các mệnh đề sau:
| Đúng | Sai | |
|---|---|---|
| a) \(MN\parallel CD\) | ||
| b) \(SA\) và \(CD\) chéo nhau | ||
| c) \(MN\parallel \left( {SCD} \right)\) | ||
| d) Mặt phẳng \(\left( {MNI} \right)\) song song với mặt phẳng \(\left( {SCD} \right)\) |
Đáp án đúng là: Đ; Đ; Đ; Đ
Đáp án cần chọn là: Đ; Đ; Đ; Đ
Cho hàm số \(f(x) = 2 + 3\cos x\) và \(g(x) = \sin x + \cos x\). Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) Giá trị lớn nhất của hàm số \(f(x)\) bằng 5 | ||
| b) Hàm số \(f(x)\) đạt giá trị nhỏ nhất khi \(x = \pi + k2\pi (k \in \mathbb{Z})\) | ||
| c) Giá trị lớn nhất của hàm số \(g(x)\) bằng \( - \sqrt 2 \) | ||
| d) Hàm số \(g(x)\) đạt giá trị nhỏ nhất khi \(x = - \dfrac{{3\pi }}{4} + k2\pi (k \in \mathbb{Z})\). |
Đáp án đúng là: Đ; Đ; S; Đ
Đáp án cần chọn là: Đ; Đ; S; Đ
Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình $x = 3\cos\left( {2t - \dfrac{\pi}{3}} \right)$. Ở đây, thời gian $t$ tính bằng giây. Các mệnh đề sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Tại thời điểm $t = 0$ là vật có li độ $x = \dfrac{3}{2}$ | ||
| b) Vật đạt biên độ cực đại lần đầu tiên tại thời điểm $t = \dfrac{\pi}{2}$ | ||
| c) Vật bắt đầu chuyển động đến khi đi qua vị trí cân bằng lần đầu tiên trong khoảng thời gian là $\dfrac{5\pi}{12}$ giây. | ||
| d) Trong thời gian từ 0 đến 30 giây, vật đi qua vị trí cân bằng 18 lần. |
Đáp án đúng là: Đ; S; Đ; S
a) Thay $t = 0$ vào hàm $x = 3\cos\left( {2t - \dfrac{\pi}{3}} \right)$ tìm li độ x
b) Vật đạt biên độ cực đại lần đầu tiên tại thời điểm $t$ sao cho $\cos\left( {2t - \dfrac{\pi}{3}} \right) = 1$ và tìm nghiệm dương nhỏ nhất.
c) Vật qua vị trí cân bằng khi $\cos\left( {2t - \dfrac{\pi}{3}} \right) = 0$ tìm nghiệm dương nhỏ nhất.
d) Tìm tất cả các nghiêm thuộc khoảng (0;30) của phương trình $\cos\left( {2t - \dfrac{\pi}{3}} \right) = 0$
Đáp án cần chọn là: Đ; S; Đ; S
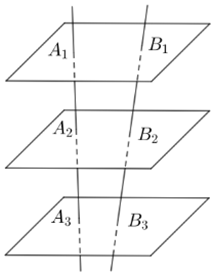
Cho ba mặt phẳng \(\left( P \right),\,\,\left( Q \right),\,\,\left( R \right)\) đôi một song song. Hai đường thẳng \(a\) và \(b\) chéo nhau cắt ba mặt phẳng \(\left( P \right),\,\,\left( Q \right),\,\,\left( R \right)\) lần lượt tại \({A_1},\,\,{A_2},\,\,{A_3}\) và \({B_1},\,\,{B_2},\,\,{B_3}\). Biết \({A_1}{A_2} = 20cm,\,\,{A_2}{A_3} = 30cm,\,\,{B_1}{B_2} = 30cm\). Tính độ dài đoạn thẳng \({B_2}{B_3}\) (đo bằng đơn vị cm).
Đáp án đúng là:
Đáp án cần điền là: 45
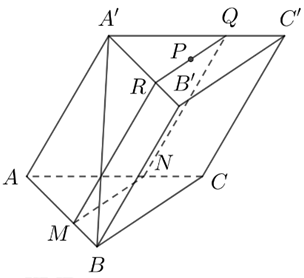
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh là 6cm. Gọi \(M,\,\,N\) là các điểm nằm trên các cạnh \(AB,\,\,AC\) thỏa mãn \(AM = AN = 4cm\), điểm \(P\) là trọng tâm của các tam giác \(A'B'C'\). Mặt phẳng \(\left( {MNP} \right)\) cắt các mặt của lăng trụ tạo thành một đa giác. Tìm số cạnh của đa giác đó.
Đáp án đúng là:
Đáp án cần điền là: 4
Phương trình $\tan\left( {2x + \dfrac{\pi}{4}} \right) = - \sqrt{3}$ có nghiệm $x = \dfrac{a\pi}{b} + \dfrac{k\pi}{2}$ ($a;k \in {\mathbb{Z}};b \in {\mathbb{N}}^{*};\dfrac{a}{b}$là phân số tối giản). Tính giá trị của biểu thức $a^{2} + b$
Đáp án đúng là:
Sử dụng công thức nghiệm của phương trình $\left. \tan x = m\Leftrightarrow x = \alpha + k\pi,k \in {\mathbb{Z}} \right.$.
Đáp án cần điền là: 73
Số nghiệm của phương trình \((\cos 3x - 1)(\tan x + \sqrt 3 ) = 0\) thuộc khoảng \((0;2024\pi )\) là
Đáp án đúng là:
Đáp án cần điền là: 4047
Tính tổng tất cả các nghiệm của phương trình $\sin 2x = \dfrac{\sqrt{2}}{2}$ trên đoạn $\lbrack 0;2\pi\rbrack$ (kết quả cuối cùng làm tròn đến hàng phần trăm).
Đáp án đúng là:
Giải phương trình lượng giác cơ bản.
Dựa vào điều kiện $x \in \lbrack 0;2\pi\rbrack$, thay các giá trị nguyên của $k$ vào các công thức nghiệm tổng quát để tìm tất cả các nghiệm nằm trong đoạn $\lbrack 0;2\pi\rbrack$
Đáp án cần điền là: 9,42
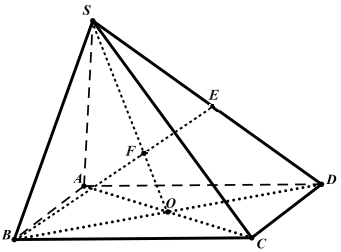
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành, tâm O. Gọi E là trung điểm của cạnh SD, gọi F là giao điểm giữa BE và mặt phẳng (SAC). Tính tỉ số $\dfrac{BE}{EF}$.
Đáp án đúng là:
Xác định giao điểm giữa đường thẳng và mặt phẳng.
CHứng minh F là trọng tâm tam giác SBD, từ đó suy ra tỉ số $\dfrac{BE}{EF}$.
Đáp án cần điền là: 3