Cho cấp số cộng $\left( u_{n} \right)$ có $u_{1} = 4;d = - 3$. Giá trị của $u_{10}$ bằng:
Đáp án đúng là: B
Công thức số hạng tổng quát của cấp số cộng.
Đáp án cần chọn là: B
Một quần thể virut Corona $P$ có $P(t)$ là số lượng virut Corona $P$ sau $t$ giờ, $t \geq 0$ và đang thay đổi với tốc độ $P'(t) = \dfrac{5000}{1 + 0,2t}$, trong đó $t$ là thời gian tính bằng giờ. Quần thể virut Corona $P$ ban đầu có số lượng là 1000 con. Số lượng virut Corona sau 3 giờ gần với số nào sau đây nhất?
Đáp án đúng là: C
Sử dụng định nghĩa của tích phân.
Đáp án cần chọn là: C
Tập nghiệm $S$ của bất phương trình $5^{x} - \dfrac{1}{5} > 0$ là:
Đáp án đúng là: A
Giải bất phương trình mũ.
Đáp án cần chọn là: A
Trong không gian Oxyz, cho điểm $A(1;2; - 1)$ và $\overset{\rightarrow}{AB} = (1;3;1)$. Tọa độ của điểm $B$ là:
Đáp án đúng là: C
Cho $A(x_1;y_1;z_1)$, $B(x_2;y_2;z_2)$, có $\overset{\rightarrow}{AB} = (x_2-x_1;y_2-y_1;z_2-z_1)$, từ đó xác định toạ độ điểm B.
Đáp án cần chọn là: C
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:

Tứ phân vị thứ ba của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
Đáp án đúng là: B
Công thức tính tứ phân vị của mẫu số liệu ghép nhóm.
Đáp án cần chọn là: B
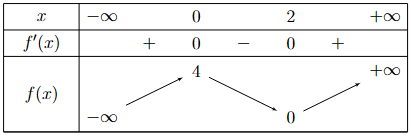
Cho hàm số $y = f(x)$ xác định trên tập $R\backslash\left\{ - 1;1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
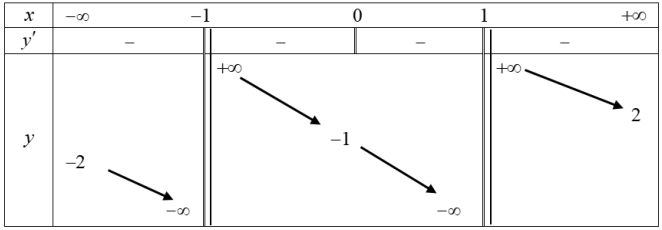
Hỏi đồ thị hàm số có bao nhiêu tiệm cận ngang?
Đáp án đúng là: A
Dựa vào bảng biến thiên và định nghĩa tiệm cận ngang.
Đáp án cần chọn là: A
Đạo hàm của hàm số \(y = {3^x}\) là:
Đáp án đúng là: B
Công thức đạo hàm
Đáp án cần chọn là: B
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
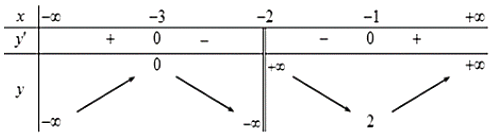
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Đáp án đúng là: B
Dựa vào bảng biến thiên.
Đáp án cần chọn là: B
Một cuộc khảo sát được thực hiện để điều tra số giờ sử dụng điện thoại và tivi của 40 học sinh lớp 11A trong một tuần. Thu được kết quả như sau:

Nhóm chứa mốt là?
Đáp án đúng là: A
Quan sát nhóm có số học sinh nhiều nhất
Đáp án cần chọn là: A
Cho hình lập phương $ABCD \cdot A_{1}B_{1}C_{1}D_{1}$. Góc giữa $AC$ và $DA_{1}$ bằng:
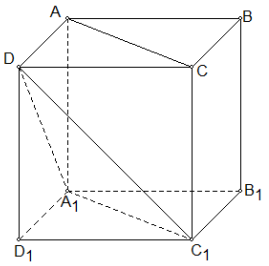
Đáp án đúng là: D
Xác định góc giữa hai đường thẳng chéo nhau.
Đáp án cần chọn là: D
Trong không gian \(Oxyz\), cho \(A\left( {0; - 1; - 1} \right)\), \(B\left( { - 2;1;1} \right)\), \(C\left( { - 1;3;0} \right)\), \(D\left( {1;1;1} \right)\). Tính cosin của góc giữa hai đường thẳng \(AB\) và \(CD\)?
Đáp án đúng là: C
Sử dụng công thức \(\cos \left( {AB;CD} \right) = \left| {\cos \left( {\overrightarrow {AB} ;\overrightarrow {CD} } \right)} \right| = \dfrac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{AB.CD}}\).
Đáp án cần chọn là: C
Trong các phương trình sau, phương trình nào vô nghiệm?
Đáp án đúng là: D
Tập giá trị của hàm lượng giác.
Đáp án cần chọn là: D
Cho hàm số \(y = f(x) = {x^3} - 3{x^2} + 4\).
| Đúng | Sai | |
|---|---|---|
| a) Hàm số \(y = f(x)\) nghịch biến trên khoảng \((0;2)\). | ||
| b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \). |
||
| c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số \(y = f(x)\). Khi đó độ dài AB bằng \(\sqrt 5 \). | ||
| d) Đồ thị hàm số \(y = \dfrac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng. |
Đáp án đúng là: Đ; Đ; S; S
Khảo sát hàm số bậc ba: Tính đạo hàm, lập bảng biến thiên, xác định khoảng biến thiên, cực trị và các đường tiệm cận.
Đáp án cần chọn là: Đ; Đ; S; S
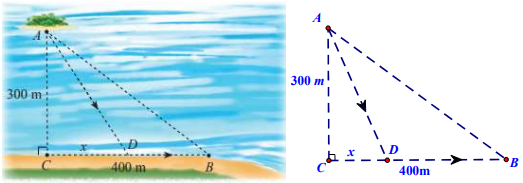
Trong một trò chơi thử thách, bạn Giáp đang ở trên thuyền (vị trí A) cách bờ hồ (vị trí C) 300 m và cần đi đến vị trí B trên bờ hồ như hình vẽ dưới đây, khoảng cách từ C đến B là 400 m . Lưu ý là Giáp có thể chèo thuyền thẳng từ A đến B hoặc chèo thuyền từ A đến một điểm nằm giữa C và B rồi chạy bộ đến B.
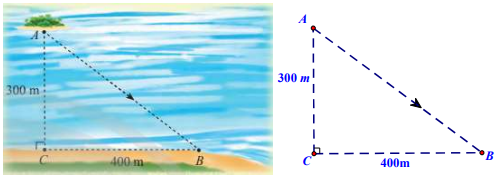
Biết rằng Giáp chèo thuyền với tốc độ \(50 \mathrm{~m} /\) phút và chạy bộ với tốc độ \(100 \mathrm{~m} /\) phút.
| Đúng | Sai | |
|---|---|---|
| a) Thời gian Giáp chèo thuyền từ A đến C rồi chạy bộ từ C đến B là 10 phút. | ||
| b) Giả sử Giáp chèo thuyền thẳng đến điểm \(D\) nằm giữa B và C và cách C một đoạn \(x(\mathrm{~m})\) như hình vẽ dưới đây, rồi chạy bộ đến B thì thời gian Giáp đi từ A đến B được tính bằng công thức \(f(x)=\dfrac{1}{100}\left(\sqrt{x^2+90000}+400-x\right)\) (phút).
|
||
| c) Thời gian nhanh nhất để Giáp đi từ A đến B xấp xỉ 9,2 phút (kết quả làm tròn đến hàng phần chục). | ||
| d) Thời gian Giáp chèo thuyền thẳng từ A đến B là 10 phút. |
Đáp án đúng là: Đ; S; Đ; Đ
Tìm quãng đường theo $x$.
Lập hàm số thời gian bằng cách sử dụng công thức $t = \dfrac{s}{v}$ cho từng chặng rồi cộng lại để được hàm tổng thời gian $f(x)$.
Khảo sát hàm số trên, tìm giá trị nhỏ nhất.
Đáp án cần chọn là: Đ; S; Đ; Đ
Một tháp trung tâm kiểm soát không lưu ở sân bay cao 80m sử dụng ra đa có phạm vi theo dõi 500km được đặt trên đỉnh tháp. Chọn hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với vị trí chân tháp, mặt phẳng \((Oxy)\) trùng với mặt đất sao cho tia \(Ox\) hướng về phía tây, tia \(Oy\) hướng về phía nam, tia \(Oz\) hướng thẳng đứng lên phía trên (Hình l) (đơn vị trên mỗi trục tính theo kilômét). Một máy bay tại vị trí A cách mặt đất 10km, cách 300km về phía đông và 200km về phía bắc so với tháp trung tâm kiếm soát không lưu

| Đúng | Sai | |
|---|---|---|
| a) Ra đa của trung tâm kiểm soát không lưu không thể phát hiện được máy bay tại vị trí \(A\). | ||
| b) Ra đa ở vị trí có toạ độ \((0;0;0,08)\). | ||
| c) Vị trí \(A\) có toạ độ \((300;200;10)\). | ||
| d) Khoảng cách từ máy bay đến ra đa là khoảng \(360,69\;{\rm{km}}\) (làm tròn kết quả đến hàng phần trăm). |
Đáp án đúng là: S; Đ; S; Đ
Xác định tọa độ của rađa, tọa độ của máy bay.
Tính khoảng cách từ rađa đến máy bay.
Đáp án cần chọn là: S; Đ; S; Đ
Một người vừa gieo một con xúc xắc để ghi lại số chấm xuất hiện, sau đó người này tiếp tục chọn ngẫu nhiên một lá bài từ bộ bài 52 lá.
| Đúng | Sai | |
|---|---|---|
| a) Gọi A là biến cố: "Số chấm của xúc xắc lớn nhất", khi đó: \({\rm{P}}(A) = \dfrac{1}{6}\). | ||
| b) Gọi B là biến cố: "Chọn được một lá bài tây (lá bài hình người)", khi đó: \({\rm{P}}(B) = \dfrac{3}{{13}}\). | ||
| c) Xác suất để số chấm trên con xúc xắc là lớn nhất và chọn được một lá bài tây bằng \(\dfrac{1}{{26}}\). | ||
| d) Coi Át là lá bài mang số 1 trong bộ bài, khi đó xác suất để số chấm trên con xúc xắc và số của lá bài là giống nhau bằng \(\dfrac{1}{{16}}\). |
Đáp án đúng là: Đ; Đ; Đ; S
Xác định tính độc lập của hai biến cố, sử dụng quy tắc nhân xác suất.
Liệt kê các cặp kết quả có thể xảy ra, tính xác suất cho từng cặp và sử dụng quy tắc cộng xác suất.
Chú ý: bộ bài 52 lá thì có 12 lá bài tây.
Đáp án cần chọn là: Đ; Đ; Đ; S
Một doanh nghiệp sản xuất độc quyền một loại sản phẩm. Giả sử khi sản xuất và bán hết $x$ sản phẩm $(0 < x \leq 300,x \in N)$, tổng số tiền doanh nghiệp thu được là $f(x) = 2500x - x^{2}$ (đơn vị: nghìn đồng) và tổng chi phí sản xuất là $g(x) = x^{2} + 1700x - 1500$ (đơn vị: nghìn đồng). Giả sử mức thuế phụ thu trên một đơn vị sản phẩm bán được là $t$ (nghìn đồng) $(0 < t < 500)$. Giá trị của $t$ bằng bao nhiêu nghìn đồng để nhà nước nhận được số tiền thuế phụ thu lớn nhất và doanh nghiệp cũng nhận được lợi nhuận lớn nhất theo mức thuế phụ thu đó?
Đáp án đúng là:
Thiết lập hàm lợi nhuận sau thuế: Lấy hàm doanh thu trừ đi hàm chi phí và trừ tiếp đi phần thuế tổng cộng ($x \cdot t$).
Tính đạo hàm của hàm lợi nhuận theo biến $x$, cho đạo hàm bằng 0 để tìm biểu thức của $x$ phụ thuộc vào $t$.
Khảo sát hàm $G(t) = x \cdot t$, trong đó $x$ là biểu thức vừa tìm được ở bước 2 vào.
Tìm giá trị $t$ để $G(t)$ lớn nhất.
Đáp án cần điền là: 400
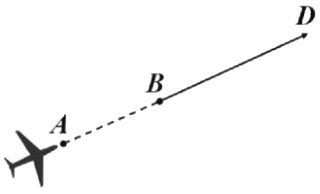
Trong không gian \(Oxyz\) (đơn vị đo lấy theo km), radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \(A(800 ; 500 ; 7)\) đến điểm \(B(940 ; 550 ; 8)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo là \(D(x ; y ; z)\). Khi đó, \(x-y+z\) bằng bao nhiêu?
Đáp án đúng là:
Nhận xét tỉ lệ vectơ. Vì máy bay giữ nguyên vận tốc và thời gian di chuyển bằng nhau (đều 10 phút) nên $\overrightarrow{AB} = \overrightarrow{BD}$.
Tìm tọa độ điểm $D$: Sử dụng công thức tính nhanh: $D = 2B - A$
Thay tọa độ $x, y, z$ vừa tìm được của $D$ vào biểu thức đề bài yêu cầu để ra kết quả.
Đáp án cần điền là: 489
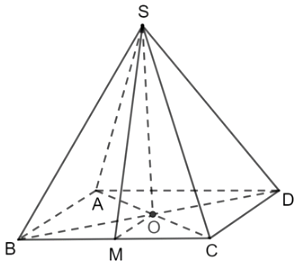
Kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98m và cạnh đáy 180m. Tính giá trị tang của góc nhị diện tạo bởi mặt bên và mặt đáy của kim tự tháp đó (làm tròn kết quả đến hàng phần chục).
Đáp án đúng là:
Vẽ hình, xác định góc nhị diện tạo bởi mặt bên và mặt đáy.
Đáp án cần điền là: 1,1
Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng theo hình thức lãi kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi suất 6%/ năm cũng theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt đầu gửi tiết kiệm là bao nhiêu triệu đồng (kết quả được làm tròn đến hàng đơn vị)?
Đáp án đúng là:
Đáp án cần điền là: 64
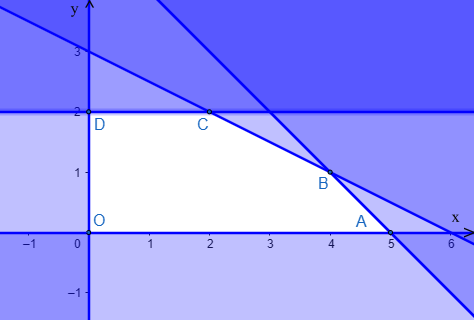
Có ba nhóm máy A, B,C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
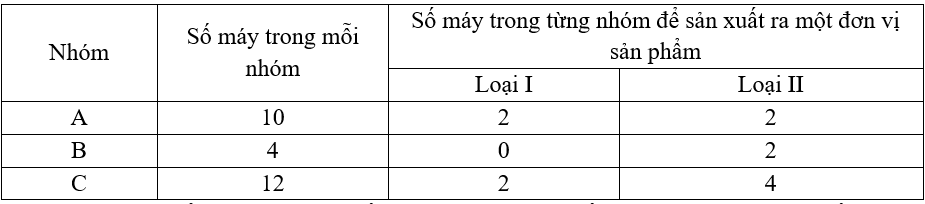
Một đơn vị sản phẩm I lãi ba nghìn đồng, một đơn vị sản phẩm loại II lãi năm nghìn đồng. Trong điều kiện sản xuất đó hãy tính số tiền lãi có thể đạt cao nhất? (tiền lãi có đơn vị nghìn đồng)
Đáp án đúng là:
Gọi $x$ là số đơn vị sản phẩm loại I và $y$ là số đơn vị sản phẩm loại II
Lập hệ bất phương trình 2 ẩn, biểu diễn miền nghiệm. Khi đó tiền lãi là $F = 3x + 5y$ lớn nhất tại 1 trong các đỉnh của đa giác miền nghiệm.
Đáp án cần điền là: 17
Trong đợt ủng hộ sách giáo khoa cho những học sinh bị ảnh hưởng do trận lũ lụt vừa qua, lớp 12A nhận được 20 cuốn gồm 5 cuốn sách Toán học, 7 cuốn sách Vật lí, 8 cuốn sách Hóa học, các sách cùng môn học là giống nhau. Số sách này được chia đều cho 10 học sinh, mỗi học sinh chỉ được nhận đúng 2 cuốn sách khác môn học. Trong số 10 học sinh nhận sách đợt này có bạn Hưng và bạn Thành. Tính xác suất để 2 cuốn sách mà bạn Hưng nhận được giống 2 cuốn sách của bạn Thành (làm tròn kết quả đến hàng phần trăm).
Đáp án đúng là:
Giải hệ phương trình từ số lượng sách mỗi môn để xác định số lượng cụ thể của 3 loại bộ sách phối hợp (Toán-Lý, Lý-Hóa, Toán-Hóa).
Sử dụng quy tắc cộng và quy tắc nhân xác suất.
Đáp án cần điền là: 0,31