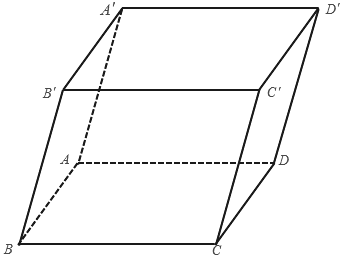
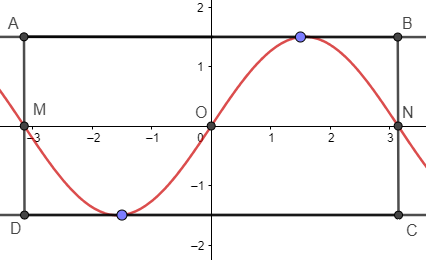
Cho hình hộp \(A B C D \cdot A'B'C'D'\) và \(G\) là trọng tâm tam giác \(B A^{\prime} D\). Mệnh đề nào sau đây đúng?
Đáp án đúng là: B
Sứ dụng quy tắc hình hộp, \(\overrightarrow{A B}+\overrightarrow{A A^{\prime}}+\overrightarrow{A D}=3 \overrightarrow{A G}\) với \(G\) là trọng tâm tam giác \(B A^{\prime} D\).
Đáp án cần chọn là: B
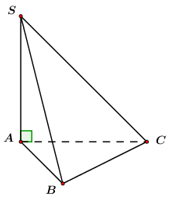
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và \(AB \bot BC.\) Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là góc nào sau đây?
Đáp án đúng là: D
Góc giữa mặt phẳng \(\left( \alpha \right)\) và mặt phẳng \(\left( \beta \right)\) là góc giữa đường thẳng \(a \subset \left( \alpha \right)\) và \(b \subset \left( \beta \right)\) sao cho \(\left\{ \begin{array}{l}a \bot d\\b \bot d\end{array} \right.\) với \(d = \left( \alpha \right) \cap \left( \beta \right).\)
Đáp án cần chọn là: D
Tập nghiệm của bất phương trình \({\rm{lo}}{{\rm{g}}_{0,5}}x > 2\) là
Đáp án đúng là: B
\({\log _a}x > b \Leftrightarrow x < {a^b}\) với \(0 < a < 1\)
Đáp án cần chọn là: B
Trong không gian \(Oxyz\), cho điểm \(M\left( { - 1;3;4} \right)\) và mặt phẳng \(\left( P \right):x - y - z + 1 = 0\). Phương trình mặt phẳng đi qua \(M\) và song song với mặt phẳng \(\left( P \right)\) là
Đáp án đúng là: D
Viết phương trình mặt phẳng biết điểm đi qua và mặt phẳng song song với nó. Hai mặt phẳng song song có hai vecto pháp tuyến cùng phương.
Đáp án cần chọn là: D
Trong không gian \(Oxyz\), cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 5 - 2t}\\{y = 3t}\\{z = 2}\end{array}} \right.\), với \(t\) là tham số. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng \(d\).
Đáp án đúng là: D
Đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = x_o + at}\\{y = y_o + bt}\\{z = z_o + ct}\end{array}} \right.\) nhận \(\overrightarrow {{u_1}} = \left( {a;b;c} \right)\) là 1 VTCP.
Đáp án cần chọn là: D
Đo chiều cao của 100 học sinh, ta thu được kết quả như bảng dưới đây. Phương sai của mẫu số liệu ghép nhóm trên là \(\overline{a, b c d e}\), với \(a,b,c,d,e\) là các số tự nhiên. Khi đó \(a + b + c + d + e\) bằng

Đáp án đúng là: D
Công thức tính phương sai của mẫu số liệu: \({s^2} = \dfrac{1}{n}\left[ {{{\left( {{x_1} - \bar x} \right)}^2} + {{\left( {{x_2} - \bar x} \right)}^2} + \ldots {{\left( {{x_n} - \bar x} \right)}^2}} \right]\)
Hoặc \({s^2} = \dfrac{1}{n}\left( {x_1^2 + x_2^2 + \ldots + x_n^2} \right) - {\bar x^2}\), trong đó \(\bar x\) là số trung bình mẫu.
Đáp án cần chọn là: D
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_{2023}} = 2\) và \({u_{2024}} = 4\). Công bội của cấp số nhân đã cho bằng
Đáp án đúng là: C
Cấp số nhân \(\left( {{u_n}} \right)\) có công bội \(q\): \(q = \dfrac{{{u_n}}}{{{u_{n - 1}}}}\).
Đáp án cần chọn là: C
Cho hàm số \(y = f\left( x \right)\) có đồ thị trong hình bên. Mệnh đề nào dưới đây đúng?
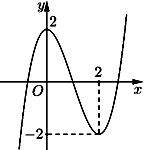
Đáp án đúng là: D
Quan sát đồ thị và kết luận
Đáp án cần chọn là: D
\(\int\limits_{ - 3}^0 {\dfrac{1}{{1 - x}}\;{\rm{d}}x} \) bằng
Đáp án đúng là: D
Nguyên hàm mở rộng: \(\int {\dfrac{1}{{ax + b}}dx} = \dfrac{1}{a}\ln \left| {ax + b} \right| + C\).
Đáp án cần chọn là: D
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau:
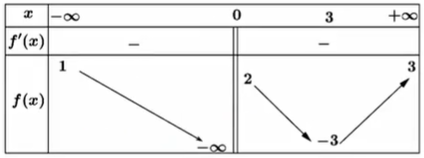
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận?
Đáp án đúng là: B
Đường thẳng \(x=a\) là đường tiệm cận đứng của đồ thị hàm \(y=f(x)\) nếu ít nhất một trong bốn điều kiện sau được thoả mãn:
\(\lim _{x \rightarrow a^{+}} f(x)=+\infty \), \(\lim _{x \rightarrow a^{+}} f(x)=-\infty \),
\(\lim _{x \rightarrow a^{-}} f(x)=+\infty \), \(\lim _{x \rightarrow a^{-}} f(x)=-\infty\)
Đường thẳng \(y=b\) là tiệm cận ngang của đồ thị hàm \(y=f(x)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\lim _{x \rightarrow+\infty} f(x)=b\), \(\lim _{x \rightarrow-\infty} f(x)=b\)
Đáp án cần chọn là: B
Phương trình \({2^{x + 2}} = {4^3}\) có nghiệm là
Đáp án đúng là: C
Đưa về cùng cơ số.
Đáp án cần chọn là: C
Cho miền phẳng $(D)$ giới hạn bởi $y = \sqrt{x}$, hai đường thẳng $x = 1$, $x = 2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $(D)$ quanh trục hoành.
Đáp án đúng là: B
Ứng dụng tích phân tính thể tích khối tròn xoay: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Đáp án cần chọn là: B
Cho hàm số \(f(x)=\sin x+\cos 2x\).
| Đúng | Sai | |
|---|---|---|
| a) \(f(0)=1\); \(f\left(\dfrac{\pi}{3}\right)=\dfrac{-1+\sqrt{3}}{2}\). | ||
| b) Đạo hàm của hàm số là \(f'(x) = \cos x-\dfrac{1}{2}\sin 2x\). | ||
| c) Phương trình \(f'(x)=0\) có nghiệm duy nhất trên đoạn \([0;\pi]\). | ||
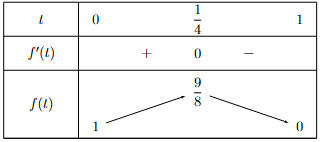
| d) Giá trị lớn nhất của \(f(x)\) trên \([0;\pi]\) là \(\dfrac{9}{4}\). |
Đáp án đúng là: Đ; S; Đ; S
a) Thay \(x=0\) và \(x=\dfrac{\pi}{3}\), xác định giá trị hàm số.
b) Tính đạo hàm hàm số lượng giác.
c) Biến đổi lượng giác: \(\cos 2x=1-2\sin^2x\). Đặt \(t=\sin x\) với \(t \in [0;1]\), giải phương trình.
d) Tìm giá trị nhỏ nhất của hàm số \(f(t)\) trên đoạn \([0;1]\).
Đáp án cần chọn là: Đ; S; Đ; S
Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian, mô tả bởi công thức \(v(t)=\dfrac{1}{{120}}{t^2}+ \dfrac{{58}}{{45}}t(\;{\rm{m}}/{\rm{s}})\), trong đó \(t\) (giây) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn 3 giây so với \(A\) và có gia tốc bằng \(a\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\) (\(a\) là hằng số). Sau khi \(B\) xuất phát được 17 giây thì đuổi kịp \(A\).
| Đúng | Sai | |
|---|---|---|
| a) Vận tốc của chất điểm B là \(\int a dt\). | ||
| b) Quãng đường chất điểm \(A\) đi từ khi xuất phát đến khi \(B\) đuổi kịp là 210m. | ||
| c) Giá trị của \(a\) là \(\dfrac{{560}}{{239}}\). | ||
| d) Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) là 25m/s. |
Đáp án đúng là: Đ; S; S; S
a) Vận tốc của chất điểm là \({v_B}(t) = \int a dt\) với \(a\) là gia tốc.
b) Quãng đường đi được từ thời điểm \(t_1\) đến \(t_2\) là tích phân của vận tốc: \(S=\int_{t_1}^{t_2} v(t) d t \).
c) Sử dụng điều kiện ban đầu của \(B\): \(v_B(3)=0\);
Tính quãng đường B đi được từ lúc bắt đầu đến khi gặp \(A\).
Giải phương trình tìm \(a\).
d) Thay giá trị \(a\) vào \(v_B(20)\).
Đáp án cần chọn là: Đ; S; S; S
Một công ty có một dây chuyền sản xuất thường xuyên mở khóa đào tạo công nhân để họ làm việc hiệu quả hơn. Có 50% công nhân mới tham gia khóa đào tạo. Thống kê cho thấy rằng có khoảng 90% công nhân tham gia khóa đào tạo sẽ làm việc đạt mức yêu cầu. Và có khoảng 65% công nhân làm việc đạt mức yêu cầu nếu không tham gia khóa đào tạo.
| Đúng | Sai | |
|---|---|---|
| a) Tham gia khóa đào tạo không ảnh hưởng đến hiệu suất làm việc của công nhân. | ||
| b) Xác suất chọn ngẫu nhiên một công nhân đạt mức yêu cầu là 77,5%. | ||
| c) Nếu một công nhân làm việc đạt mức yêu cầu, xác suất người đó đã tham gia khóa đào tạo là lớn hơn 40%. | ||
| d) Công ty quyết định tổ chức một buổi kiểm tra năng lực để đánh giá các công nhân. Trong số các công nhân đạt mức yêu cầu, có 80% số người vượt qua buổi kiểm tra này. Trong khi đó, trong số các công nhân làm việc không đạt mức yêu cầu, chỉ có 30% số người vượt qua kiểm tra. Nếu một công nhân không vượt qua buổi kiểu tra thì xác suất công nhân đó làm việc đạt mức yêu cầu là 49,6%. |
Đáp án đúng là: S; Đ; Đ; Đ
Gọi biến cố A: “Công nhân tham gia khóa đào tạo”.
B: “Công nhân làm việc đạt mức yêu cầu”.
C: “Công nhân vượt qua buổi kiểm tra”
a) Dựa vào dữ kiện đầu bài.
b) Áp dụng công thức xác suất toàn phần để tính \(P(B).\)
c) Áp dụng công thức Bayes để tính \(P\left( {A|B} \right)\).
d) Tính \(P\left( C \right)\), \(P\left( {\overline C } \right)\) và áp dụng công thức Bayes để tính \(P\left( {B|\overline C } \right)\).
Đáp án cần chọn là: S; Đ; Đ; Đ
Với hệ trục tọa độ Oxyz (đơn vị km), sao cho \(O\) nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, một vệ tinh dò tìm được đặt tại điểm S cách mặt nước biển 10km, cách mặt phẳng (Oxz), (Oyz) lần lượt là 4km và 3km. Vệ tinh này có khả năng phát hiện các vật thể trong phạm vi bán kính 12km. Một tàu ngầm bị mất liên lạc đang di chuyển trên đường thẳng \(\Delta \) có phương trình tham số: \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = - 2 + 2t}\\{z = - 5 - 5t}\end{array}} \right., t \in \mathbb{R}\). Một máy dò cứu hộ được triển khai tại vị trí \(M\left( {7;3;0} \right)\) và phát hiện tín hiệu một lần từ tàu ngầm khi tàu ngầm ở gần nhất.
| Đúng | Sai | |
|---|---|---|
| a) Vệ tinh dò tìm được đặt tại điểm \(S(10;4;3)\) | ||
| b) Phương trình mô tả vùng dò tìm của vệ tinh là \({(x - 3)^2} + {(y - 4)^2} + {(z - 10)^2} = 144.\) |
||
| c) Vệ tinh có khả năng phát hiện ra tàu ngầm. | ||
| d) Máy dò cứu hộ M phát hiện tín hiệu khi tàu ngầm ở vị trí \(B(7; - 3; - 7)\) |
Đáp án đúng là: S; Đ; Đ; S
a) Xác định tọa độ điểm S.
b) Viết phương trình mặt cầu tâm S , bán kính R.
c) Sử dụng công thức tính khoảng cách từ điểm đến đường thẳng.
d) Tham số hoá tọa độ điểm \(B \in \Delta\), để tàu ngầm gần máy dò nhất thì khoảng cách từ B đến M nhỏ nhất.
Đáp án cần chọn là: S; Đ; Đ; S
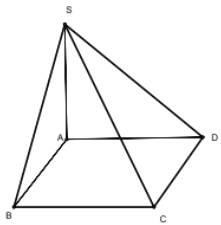
Cho hình chóp \(S \cdot A B C D\) có đáy \(ABCD\) là hình vuông với đường chéo \(AC=2\), \(S A\) vuông góc với mặt phẳng \((A B C D)\). Khoảng cách giữa hai đường thẳng \(SB\) và \(CD\) là (kết quả làm tròn đến hàng phần trăm).
Đáp án đúng là:
Khoảng cách giữa SB và CD bằng khoảng cách giữa \((S A B)\) và CD và bằng DA.
Đáp án cần điền là: 1,41
Một nhân viên giao hàng có nhiệm vụ giao bưu kiện tại 4 địa điểm: A, B, C, D. Để tiết kiệm thời gian, anh ta cần tìm lộ trình đi qua cả 4 địa điểm, không lặp lại địa điểm nào, và quay trở lại điểm xuất phát. Thời gian di chuyển giữa các địa điểm được cho như sau:
AB: 16 phút, AC: 10 phút, AD: 10 phút, BC: 19 phút, BD: 6 phút, CD: 5 phút.
Hỏi thời gian tối thiểu để hoàn thành chuyến giao hàng là bao nhiêu?
Đáp án đúng là:
Đáp án cần điền là: 37
Trong không gian với hệ toạ độ Oxyz, cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(A(0;0;0)\), \(B(3;0;0),D(0;3;0),{D^\prime }(0;3; - 3)\). Tổng hoành độ và cao độ của trọng tâm tam giác \({A^\prime }{B^\prime }C\) là?
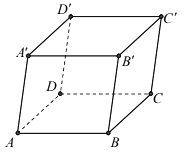
Đáp án đúng là:
Dựa vào tính chất hình bình hành, xác định tọa độ các điểm \(A',B', C\).
G là trọng tâm tam giác \(A^{\prime} B^{\prime} C,\left\{\begin{array}{l}x_G=\dfrac{x_{A^{\prime}}+x_{B^{\prime}}+x_C}{3} \\ y_G=\dfrac{y_{A^{\prime}}+y_{B^{\prime}}+y_C}{3} \\ z_G=\dfrac{z_{A^{\prime}}+z_{B^{\prime}}+z_C}{3}\end{array}\right.\)
Đáp án cần điền là: 0
Bác An có mảnh vườn hình chữ nhật \(ABCD\), chiều dài \(AB = 2\pi \left( m \right)\), chiều rộng \(BC = 3\left( m \right)\). Bác muốn trồng hoa trên dải đất (phần tô đậm) được giới hạn bởi đường \(MN\) (với \(M,N\) lần lượt là trung điểm của \(AD,BC\)) và một đường hình sin (tham khảo hình vẽ). Diện tích đất trồng hoa bằng bao nhiên \(m^2\)?
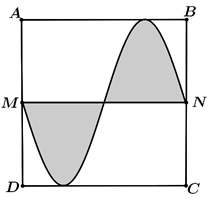
Đáp án đúng là:
Gắn hệ toạ độ Oxy với O là trung điểm của MN.
Xác định phương trình của đường cong.
Ứng dụng tích phân tính diện tích hình phẳng.
Đáp án cần điền là: 6
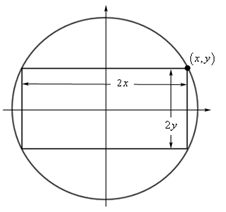
Một kiến trúc sư muốn thiết kế một khung cửa sổ hình chữ nhật lắp vào một ô tròn trên tường có bán kính 4 mét. Kiến trúc sư muốn cửa sổ có kích thước lớn nhất để đón ánh sáng vào căn phòng. Hỏi diện tích lớn nhất của cửa sổ có thể đạt được là bao nhiêu?
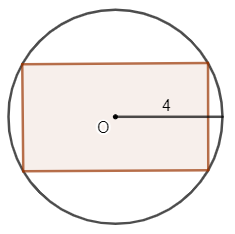
Đáp án đúng là:
- Bài toán yêu cầu tìm diện tích lớn nhất của hình chữ nhật nội tiếp hình tròn có bán kính bằng 4.
- Đặt trục tọa độ với tâm đường tròn trùng với gốc tọa độ. Lập phương trình đường tròn và biểu
diễn hàm diện tích của hình chữ nhật.
- Tính đạo hàm của hàm diện tích và tìm giá trị lớn nhất của hàm số.
Đáp án cần điền là: 32
Cơ quan tình báo Trung ương Mỹ (CIA) đã thử nghiệm một loại thuốc nói thật, được gọi là “huyết thanh nói thật” (Truth serum) với mục đích thẩm vấn các nghi phạm khủng bố. Hiệu quả của loại thuốc này được xác định bởi mức độ chính xác mà nó có thể phân biệt giữa nghi phạm có tội và vô tội. 90% nghi phạm có tội được phán đoán đúng. Tuy nhiên, vẫn có 1% khả năng nghi phạm vô tội bị phán đoán sai. Nếu chọn một nghi phạm từ một nhóm người có 5% người phạm tội và huyết thanh nói thật cho rằng anh ta có tội, vậy xác suất nghi phạm này vô tội là bao nhiêu %? Kết quả làm tròn đến hàng phần mười.
Đáp án đúng là:
Gọi các biến cố: A: “Nghi phạm có tội”.
B: “Thuốc cho kết quả nghi phạm có tội”.
Cần tính \(P\left( {\overline A |B} \right)\).
Xác định các xác suất đã cho và áp dụng công thức xác suất toàn phần, công thức Bayes để tính \(P\left( {\overline A |B} \right)\).
Đáp án cần điền là: 17,4