Phát biểu nào sau đây không đúng
Đáp án đúng là: D
Lý thuyết về nội năng của một vật.
Đáp án cần chọn là: D
Biểu thức nào sau đây thể hiện đúng mối liên hệ giữa đơn vị T của cảm ứng từ với các đơn vị N của lực từ, A của cường độ dòng điện và m của chiều dài?
Đáp án đúng là: A
Lý thuyết về đơn vị cảm ứng từ.
Đáp án cần chọn là: A
Theo phương trình trạng thái của khí lí tưởng, tích của áp suất p và thể tích V của một khối lượng khí lí tưởng xác định
Đáp án đúng là: B
Áp dụng lý thuyết về phương trình trạng thái khí lí tưởng.
Đáp án cần chọn là: B
Ứng dụng nào sau đây không phải là ứng dụng của đồng vị phóng xạ?
Đáp án đúng là: B
Lý thuyết về ứng dụng của đồng vị phóng xạ.
Đáp án cần chọn là: B
Một đứa trẻ bị sốt, người mẹ đã sử dụng thiết bị (hình vẽ) để đo nhiệt độ kết quả máy đo hiển thị 1010F (do máy hỏng thang đo Celsius).
Trả lời cho các câu 5, 6, 7 dưới đây:
Thiết bị đo nhiệt độ cho bé được gọi là:
Đáp án đúng là: C
Lý thuyết về dụng cụ đo nhiệt độ.
Đáp án cần chọn là: C
Đứa trẻ khi sốt có nhiệt độ trong thang Celsius là
Đáp án đúng là: D
Cách chuyển giữa thang đo nhiệt độ Cesius và thang đo nhiệt độ Fahrenheit.
Đáp án cần chọn là: D
Đứa trẻ được mẹ cho uống thuốc hạ sốt, cơn sốt hạ xuống 980F trong 20 phút. Giả sử cơ chế bay hơi của mồ hôi là cách duy nhất để làm giảm nhiệt độ cơ thể. Khối lượng của đứa trẻ là 30kg. Nhiệt dung riêng của cơ thể con người gần bằng nhiệt dung riêng của nước là 1000cal/kg.0C và nhiệt hoá hơi của nước khoảng 580cal/g, thì tốc độ bay hơi trung bình do thuốc gây ra là bao nhiêu?
Đáp án đúng là: A
- Cần đổi nhiệt độ Fahrenheit về nhiệt độ Celsius.
- Áp dụng công thức trao đổi nhiệt lượng giữa cơ thể trẻ và nhiệt lượng làm hóa hơi nước.
- Tốc độ bay hơi trung bình do thuốc gây ra: \(\dfrac{{{m_{hh}}}}{t}.\)
Đáp án cần chọn là: A
Biết nhiệt nóng chảy riêng của đồng là \(1,{8.10^5}J/kg\), của chì là \(0,{25.10^5}J/kg\). Nhiệt lượng cần thiết để làm nóng chảy hoàn toàn 1 kg đồng ở nhiệt độ nóng chảy có thể làm nóng chảy được bao nhiêu kilôgam chì?
Đáp án đúng là: C
Áp dụng công thức tính nhiệt lượng cần để làm các chất nóng chảy ở nhiệt độ nóng chảy.
Đáp án cần chọn là: C
Cho khối lượng của proton, notron và hạt nhân \(_2^4He\)lần lượt là: 1,0073u; 1,0087u và 4,0015u. Biết 1uc2 = 931,5MeV. Năng lượng liên kết của hạt nhân \(_2^4He\)là
Đáp án đúng là: B
Lý thuyết về hạt nhân nguyên tử.
Đáp án cần chọn là: B
Động năng chuyển động tịnh tiến trung bình của phân tử tăng gấp đôi nếu
Đáp án đúng là: B
Sử dụng công thức: \({{\rm{W}}_d} = \dfrac{3}{2}kT \Rightarrow {{\rm{W}}_d} \sim T\)
Đáp án cần chọn là: B
Để đo khối lượng nguyên tử, phân tử, thế giới sử dụng đơn vị khối lượng nguyên tử amu (Atomic mass unit) với quy ước 1 đơn vị amu bằng
Đáp án đúng là: D
Lý thuyết về khối lượng hạt nhân.
Đáp án cần chọn là: D
Một khối khí ban đầu có các thông số trạng thái là \({p_0};{V_0};{T_0}.\) Biến đổi đẳng áp đến \(2{V_0}\) sau đó nén đẳng nhiệt về thể tích ban đầu. Đồ thị nào sau đây diễn tả đúng quá trình trên?

Đáp án đúng là: C
Sử dụng đồ thị của các đẳng quá trình trong các hệ trục tọa độ.
Đáp án cần chọn là: C
Các phân tử ôzôn trong tầng bình lưu hấp thụ phần lớn bức xạ có hại từ mặt trời. Thông thường, nhiệt độ và áp suất riêng phần của ôzôn trong tầng bình lưu lần lượt là 250 K và 0,0010 atm. Giả sử khí này là khí lý tưởng.
Trả lời cho các câu 13, 14 dưới đây:
Nhiệt độ của ozon trong tầng bình lưu là bao nhiêu độ Celsius?
Đáp án đúng là: B
Đổi từ độ Kelvin sang độ Celsius: \(t\left( {^oC} \right) = T\left( K \right) - 273\)
Đáp án cần chọn là: B
Có bao nhiêu phân tử ôzôn có trong 1,0 lít không khí trong những điều kiện này?
Đáp án đúng là: C
Sử dụng phương trình: \(pV = nRT = \dfrac{N}{{{N_A}}}RT.\)
Đáp án cần chọn là: C
Chất phóng xạ X có chu kỳ bán rã là T. Ban đầu có một mẫu X nguyên chất với khối lượng 60g. Sau khoảng thời gian 2T, khối lượng chất X trong mẫu đã bị phân rã là
Đáp án đúng là: D
Khối lượng chất X đã bị phân rã: \(\Delta m = {m_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)
Đáp án cần chọn là: D
Mạng điện sinh hoạt ở Nhật Bản có hiệu điện thế hiệu dụng là 110V trong khi ở Việt Nam ta là 220V. Chiếc đài Sony xách tay từ Nhật Bản về nước ta phải được gắn thêm một máy biến áp nhỏ có tổng số 2400 vòng dây. Cuộn sơ cấp của máy biến áp này có số vòng dây là:
Đáp án đúng là: A
Sử dụng công thức: \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
Đáp án cần chọn là: A
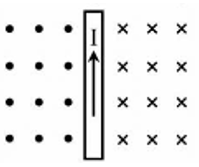
Một dây dẫn thẳng dài nằm trên trang giấy có dòng điện I chạy qua. Hình nào dưới đây mô tả cảm ứng từ của từ trường do dòng điện gây nên trên trang giấy là đúng nhất?
Đáp án đúng là: A
Áp dụng quy tắc nắm bàn tay phải xác định chiều của đường sức từ do dòng điện thẳng dài gây ra: Nắm bàn tay phải sao cho ngón tay cái chỉ chiều của dòng điện, bốn ngón tay khum lại chỉ chiều của đường sức từ.
Đáp án cần chọn là: A
Một đoạn dây dẫn uốn thành một vòng tròn tâm O, bán kính 5,8cm. Khi cho dòng điện không đổi có cường độ I chạy trong vòng dây thì dòng điện này gây ra tại O cảm ứng từ có độ lớn \(2,{6.10^{ - 5}}T\). Giá trị của I là
Đáp án đúng là: A
Sử dụng công thức tính cảm ứng từ gây ra bởi các đoạn dây dẫn có hình dạng đặc biệt.
Đáp án cần chọn là: A
Một nhóm học sinh thực hiện thí nghiệm đo nhiệt nóng chảy riêng của nước đá bằng dụng cụ thực hành. Họ chuẩn bị các dụng cụ gồm: Chai nước (1); bình nhiệt lượng kế (2) cách nhiệt (có que khuấy); cốc nước cùng các viên nước đá (3); cân điện tử (4) có độ chính xác là 0,01 g; nhiệt kế điện tử (5) có độ chính xác là 0,10C (hình bên).

Họ đã tiến hành thí nghiệm, kết quả thu được như sau:
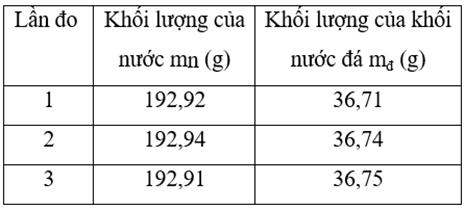
- Cân khối lượng nước và nước đá (ở 0,00C), kết quả các lần cân như bảng bên.
- Nhiệt độ ban đầu của nước và bộ dụng cụ kèm theo (bình nhiệt lượng kế, nhiệt kế, que khuấy) là t0 = 32,00C.
- Nhiệt độ của nước trong bình nhiệt lượng kế ổn định khi nước đá vừa tan hết là t = 15,50C.
Nhóm học sinh đã xác định được nhiệt dung (nhiệt lượng cần cung cấp cho vật để tăng nhiệt độ thêm 1,00C) của bộ dụng cụ kèm theo (gồm bình nhiệt lượng kế, nhiệt kế, que khuấy) là C0 = 41,9 J/K. Nhiệt dung riêng của nước là 4180 J/kg.K.
| Đúng | Sai | |
|---|---|---|
| a) Trình tự thí nghiệm: Cân khối lượng của nước rồi cho vào nhiệt lượng kế; Đo nhiệt độ ban đầu của nước và bộ dụng cụ kèm theo; Cân khối lượng của khối nước đá rồi cho vào nhiệt lượng kế; Đo nhiệt độ ổn định của nước khi nước đá vừa tan hết. | ||
| b) Để giữ cho nhiệt độ nóng chảy của nước đá không thay đổi trong suốt quá trình thí nghiệm phải giữ áp suất tác dụng lên viên đá không đổi. |
||
| c) Kết quả phép đo khối lượng nước sử dụng trong thí nghiệm là \({m_n} = 192,92 \pm 0,01g\) |
||
| d) Giá trị trung bình của nhiệt nóng chảy riêng của nước đá ở nhiệt độ 0,00C đo được bởi nhóm học sinh này là 3,16.105 J/kg. |
Đáp án đúng là: S; Đ; Đ; Đ
- Lý thuyết về thí nghiệm đo nhiệt dung riêng.
- Công thức tính giá trị trung bình và sai số của phép đo, cách ghi kết quả đo.
- Áp dụng phương trình cân bằng nhiệt.
Đáp án cần chọn là: S; Đ; Đ; Đ
Người ta dùng một bơm tay có ống bơm dài 50 cm và đường kính trong 4 cm để bơm không khí vào một túi cao su sao cho túi phồng lên. Sau 40 lần bơm thì không khí trong túi có thể tích là 6,28 lít. Biết áp suất khí quyển là 1 atm và coi nhiệt độ của không khí được bơm vào túi không đổi. Lấy \(\pi = 3,14\).
| Đúng | Sai | |
|---|---|---|
| a) Mỗi lần bơm ta đưa vào quả bóng 0,628 lít khí. |
||
| b) Sau 40 lần bơm ta đưa vào quả bóng 50,24 lít khí. |
||
| c) Sau 40 lần bơm lượng khí đưa vào quả bóng được nén còn 6,28 lít. | ||
| d) Áp suất khí trong quả bóng sau 40 lần bơm là 4 atm. |
Đáp án đúng là: Đ; S; Đ; Đ
+ Sử dụng công thức tính thể tích: V = S.h
+ Áp dụng định luật Boyle: pV = const.
Đáp án cần chọn là: Đ; S; Đ; Đ
Hình bên biểu diễn một thanh dẫn điện MN trượt trên hai thanh kim loại theo chiều vuông góc với cảm ứng từ. Biết B = 0,40T, MN = PQ = 0,20m. Thanh MN đang chuyển động về bên trái với vận tốc có độ lớn 0,2m/s và có hướng vuông góc với nó. Toàn bộ mạch điện có điện trở 2,0Ω. Các thanh kim loại không nhiễm từ, bỏ qua ma sát.
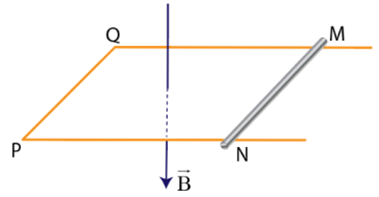
| Đúng | Sai | |
|---|---|---|
| a) Suất điện động cảm ứng trong khung dây có độ lớn là 0,016V. | ||
| b) Dòng điện trong mạch có chiều NMQP. |
||
| c) Lực kéo thanh MN chuyển động đều với tốc độ đã cho là \(6,{4.10^{ - 4}}N.\) | ||
| d) Nếu coi NM là nguồn điện thì M đóng vai trò cực dương. |
Đáp án đúng là: Đ; S; Đ; S
+ Độ lớn suất điện động cảm ứng:
\(e = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{B.\Delta S.\cos \alpha }}{{\Delta t}}} \right|\) với \(\Delta S = MN.s = MN.v.\Delta t\)
+ Áp dụng quy tắc nắm tay phải xác định chiều dòng điện.
+ Sử dụng công thức: \(F = BIl\sin \alpha \)
+ Dòng điện đi ra cực dương, đi vào cực âm.
Đáp án cần chọn là: Đ; S; Đ; S
Đồng vị phóng xạ Xenon \(_{54}^{133}Xe\)được sử dụng trong phương pháp nguyên tử đánh dấu của y học hạt nhân khi kiểm tra chức năng và chẩn đoán các bệnh về phổi. Chu kì bán rã của xenon \(_{54}^{133}Xe\) là 5,24 ngày. Một mẫu khí chứa xenon \(_{54}^{133}Xe\) khi được sản xuất tại nhà máy có độ phóng xạ 4,25.109 Bq. Mẫu đó được vận chuyển về bệnh viện và sử dụng cho bệnh nhân sau đó 3,00 ngày.
| Đúng | Sai | |
|---|---|---|
| a) Sản phẩm phân rã của xenon \(_{54}^{133}Xe\) là cesium \(_{55}^{133}Cs.\) | ||
| b) Hằng số phóng xạ của xenon \(_{54}^{133}Xe\) là 0,132 s-1. |
||
| c) Số nguyên tử \(_{54}^{133}Xe\) có trong mẫu mới sản xuất là 2,78.1015 nguyên tử. |
||
| d) Khi bệnh nhân sử dụng, độ phóng xạ của mẫu khí là 1,86.109 Bq. |
Đáp án đúng là: Đ; S; Đ; S
- Viết phương trình phản ứng hạt nhân rồi áp dụng định luật bảo toàn điện tích và bảo toàn ssoo nucleon.
- Áp dụng công thức tính hằng số phóng xạ \(\left( {\lambda = \dfrac{{\ln 2}}{T}} \right)\) và độ phóng xạ \(\left( {H = {H_0}{{.2}^{ - \dfrac{t}{T}}}} \right)\).
Đáp án cần chọn là: Đ; S; Đ; S
Người ta cung cấp nhiệt lượng 5,3 J cho khối khí trong xilanh, khí nở ra với áp suất không đổi bằng 1,1.105 N/m3. Khi đó, thể tích khí tăng thêm 20 cm3. Độ biến thiên nội năng của khối khí bằng bao nhiêu joule (jun) (làm tròn kết quả đến chữ số hàng phần mười)?
Đáp án đúng là:
Độ biến thiên nội năng của khí: $\Delta U = Q + A.$
Đáp án cần điền là: 3,1
Bạc có nhiệt nóng chảy riêng 105 kJ/kg.K. Để làm nóng chảy hoàn toàn 0,26 kg bạc ở nhiệt độ nóng chảy của nó, cần một nhiệt lượng bao nhiêu kilojoule (ki-lô-jun) (làm tròn kết quả đến chữ số hàng phần mười)?
Đáp án đúng là:
Nhiệt lượng cung cấp cho quá trình nóng chảy: $Q = m\lambda.$
Đáp án cần điền là: 27,3
Một khí cầu có dung tích 328 m3 bắt đầu được bơm khí Hydrogen. Đến khi bơm xong thì Hydrogen trong khí cầu có nhiệt độ \({27^0}C\), áp suất 0,9 atm. Biết rằng mỗi giây bơm được 2,5 g Hydrongen vào khí cầu, thời gian bơm là bao nhiêu phút?
Đáp án đúng là:
- Áp dụng phương trình Clapeyron: \(pV = nRT\)
- Thời gian bơm: \(t = \dfrac{m}{{{m_0}}}\)
Đáp án cần điền là: 160
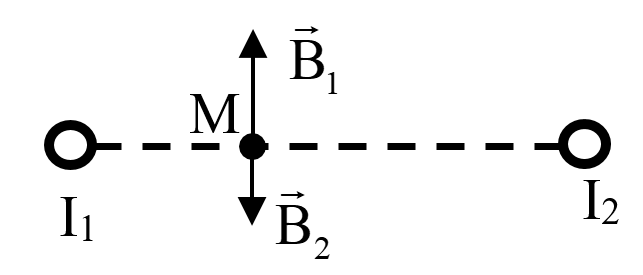
Cho hai dây dẫn thẳng, song song, cách nhau 15 cm, mang dòng điện cùng chiều, có cường độ lần lượt là I1 = 5 (A), I2 = 8 (A). Cho biết cảm ứng từ do dòng điện thẳng cường độ I (A) gây ra tại điểm cách nó khoảng r (m) được tính theo biểu thức $B = 2.10^{7}.\dfrac{I}{r}(T)$. Cảm ứng từ tổng hợp do hai dòng điện I1, I2 gây ra tại vị trí cách I1 5 cm và cách I2 10 cm là bao nhiêu $\mu T$?
Đáp án đúng là:
- Tính cảm ứng từ do các dòng điện gây ra tại điểm tổng hợp theo công thức.
- Xác định hướng của vecto cảm ứng từ theo quy tắc nắm bàn tay phải.
- Áp dụng công thức tổng hợp vecto: $\overset{\rightarrow}{B} = {\overset{\rightarrow}{B}}_{1} + {\overset{\rightarrow}{B}}_{2}$
Đáp án cần điền là: 4
Một máy phát điện xoay chiều một pha có phần ứng gồm bốn cuộn dây giống nhau mắc nối tiếp. Suất điện động xoay chiều do máy phát sinh ra có tần số 50 Hz và giá trị hiệu dụng bằng \(50\sqrt 2 \) V. Biết từ thông cực đại qua mỗi vòng của phần ứng là \(\dfrac{1}{\pi }\) mWb . Số vòng dây của mỗi cuộn dây phần ứng là
Đáp án đúng là:
Sử dụng công thức: \({E_0} = N\omega {\Phi _0}\)
Đáp án cần điền là: 250
Một mẫu vật liệu đất hiếm có chứa đồng vị phóng xạ của nguyên tố Prometi (Pm) và Galodi (Gd). Chu kì bán rã của \(^{145}Pm\) là 17,7 năm và của \(^{148}Gd\) là 85 năm. Tại thời điểm ban đầu, phân tích thành phần nguyên tố trong mẫu vật liệu cho thấy hàm lượng nguyên tử đồng vị \(^{145}Pm\) gấp đôi của \(^{148}Gd\). Hỏi sau thời gian bao lâu thì hàm lượng của hai đồng vị đó trong mẫu vật liệu là bằng nhau? (Làm tròn đến 1 chữ số sau dấu thập phân).
Đáp án đúng là:
Số hạt nhân còn lại sau thời gian t: \(N = {N_0}{.2^{\dfrac{{ - t}}{T}}}.\)
Đáp án cần điền là: 22,4