
Trong đơn vị SI, đơn vị nào là đơn vị dẫn xuất?
Đáp án đúng là: B
7 đơn vị cơ bản là: mét (m), kilogam (kg), giây (s), Ampe (A), Kelvin (K), mol (mol), candela
Đơn vị dẫn xuất là đơn vị đo lường được dẫn xuất từ 7 đơn vị cơ bản
Đáp án cần chọn là: B
Khi sử dụng các thiết bị nhiệt và thủy tinh trong phòng thí nghiệm Vật lí chúng ta cần lưu ý điều gì?
Đáp án đúng là: C
Sử dụng lý thuyết an toàn trong phòng thực hành
Đáp án cần chọn là: C
Câu nào sai khi nói về sai số tuyệt đối của phép đo trực tiếp một đại lượng vật lý
Đáp án đúng là: D
Sử dụng lý thuyết sai số tuyệt đối
Đáp án cần chọn là: D
Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là:
Đáp án đúng là: D
Lý thuyết về chuyển động biến đổi đều.
Đáp án cần chọn là: D
Sự rơi tự do là
Đáp án đúng là: A
Lý thuyết về sự rơi tự do.
Đáp án cần chọn là: A
Gọi \(\overrightarrow d \) là độ dịch chuyển và \(\overrightarrow v \) là vận tốc trung bình của một chất điểm trong khoảng thời gian t thì
Đáp án đúng là: A
Vận tốc trung bình: \(\overrightarrow v = \dfrac{{\overrightarrow d }}{t}\)
Đáp án cần chọn là: A
Đơn vị nào sau đây không phải đơn vị cơ bản của hệ SI là:
Đáp án đúng là: C
Sử dụng lý thuyết đơn vị của bản của hệ SI
Đáp án cần chọn là: C
Chọn câu đúng. Gia tốc là một đại lượng
Đáp án đúng là: C
Sử dụng lý thuyết gia tốc
Đáp án cần chọn là: C
Cho hai chuyển động thẳng được mô tả bằng hai đồ thị tương ứng như hình H1 và H2 sau. Tính chất chuyển động tương ứng với H1 và H2 lần lượt là:
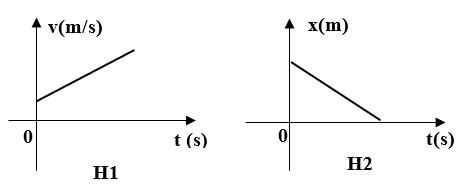
Đáp án đúng là: D
Giá trị vận tốc bằng độ dốc của đồ thị độ dịch chuyển – thời gian
Giá trị gia tốc bằng độ dốc của đồ thị vận tốc – thời gian
Đáp án cần chọn là: D
Một vật rơi tự do không vận tốc ban đầu từ độ cao 5m xuống. Lấy \(g = 10{\rm{m/}}{{\rm{s}}^2}\) Vận tốc của nó ngay trước khi chạm đất là
Đáp án đúng là: D
Sử dụng kiến thức về sự rơi tự do.
Đáp án cần chọn là: D
Một vật rơi tự do không vận tốc đầu ở nơi \(g = 10\,\,m/{s^2}\). Khi rơi được 20 m thì thời gian rơi là:
Đáp án đúng là: C
Quãng đường vật rơi tự do: \(s = \dfrac{1}{2}g{t^2}\)
Đáp án cần chọn là: C
Một vật đang ở độ cao h so với mặt đất được ném theo phương ngang với tốc độ ban đầu \({v_0}\) thì tầm xa của vật đạt L. Bỏ qua sức cản không khí và xem như gia tốc rơi tự do là không đổi. Khi ném vật với tốc độ ban đầu \(3{v_0}\) và để vật đạt tầm xa là 1,5L thì phải đưa vật đến vị trí có độ cao so với mặt đất là
Đáp án đúng là: A
Tầm xa của chuyển động ném ngang: \(L = {v_0}\sqrt {\dfrac{{2h}}{g}} \)
Đáp án cần chọn là: A
Trong các đặc điểm sau đây của quãng đường và độ dịch chuyển của một vật chuyển động, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Quãng đường có phương và chiều xác định. | ||
| b) Quãng đường không thể có độ lớn bằng 0. | ||
| c) Độ dịch chuyển có thể có độ lớn bằng 0. | ||
| d) Độ dịch chuyển chỉ có đơn vị là mét. |
Đáp án đúng là: S; Đ; Đ; S
Độ dịch chuyển là một đại lượng vecto, quãng đường là đại lượng vô hướng
Đáp án cần chọn là: S; Đ; Đ; S
Một quả bóng được ném với tốc độ 8,2 m/s theo phương ngang từ đỉnh của một tòa nhà, như hình vẽ. Mặt bên của tòa nhà là thẳng đứng. Tại một điểm Đ trên đường đi của mình, quả bóng cách mặt bên tòa nhà một khoảng x, có vận tốc hợp với phương ngang góc \({60^0}\). Bỏ qua lực cản của không khí, lấy \(g = 9,8\,\,m/{s^2}\).
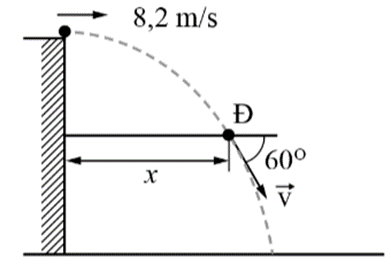
| Đúng | Sai | |
|---|---|---|
| a) Độ lớn thành phần thẳng đứng của vận tốc tại điểm Đ là 4,7 m/s. | ||
| b) Độ lớn của vận tốc tại điểm Đ là 16,4 m/s. | ||
| c) Khoảng cách mà quả bóng đã rơi theo phương thẳng đứng tại điểm Đ là 10,3 m. | ||
| d) Khoảng cách x theo phương nằm ngang tại điểm Đ là 10,9 m. |
Đáp án đúng là: S; Đ; Đ; S
Sử dụng các công thức lượng giác trong tam giác vuông
Vận tốc theo phương ngang của chuyển động ném ngang: \({v_x} = {v_0}\)
Vận tốc theo phương thẳng đứng của chuyển động ném ngang: \({v_y} = gt\)
Quãng đường theo phương thẳng đứng của chuyển động ném ngang: \(h = \dfrac{1}{2}g{t^2}\)
Quãng đường theo phương ngang của chuyển động ném ngang: \(L = {v_x}t\)
Đáp án cần chọn là: S; Đ; Đ; S
Khi dùng Ứng dụng Google maps để tìm đường đi từ trường THPT Kim Sơn A đến trường THPT Bình Minh (huyện Kim Sơn, tỉnh Ninh Bình), trên điện thoại thông minh, ứng dụng hiển thị kết quả như hình bên.
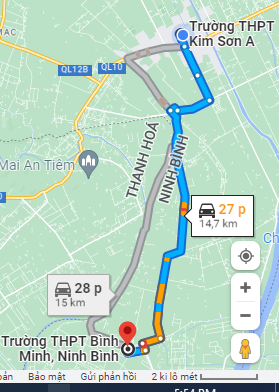
Phần mềm dự đoán lộ trình tối ưu khi di chuyển bằng ô tô hết mất quãng đường bao nhiêu km?
Đáp án đúng là:
Sử dụng khả năng đọc dữ kiện trên bản đồ.
Đáp án cần điền là: 14,7
Một người đi bộ từ nhà đến bến xe bus cách nhà 1 km về phía Tây. Đến bến xe, người đó lên xe bus đi tiếp 5 km về phía Nam. Quãng đường người đó đi được trong cả chuyến đi là bao nhiêu km?
Đáp án đúng là:
Tổng quãng đường: \(s = {s_1} + {s_2}\)
Đáp án cần điền là: 6
Một người chèo thuyền qua một con sông rộng 400 m. Muốn cho thuyền đi theo đường AB, người đó phải luôn hướng mũi thuyền theo hướng AC (hình vẽ). Biết thuyền qua sông hết 8 min 20 s và vận tốc chảy của dòng nước là 0,6 m/s. Tìm vận tốc của thuyền so với dòng nước. (Đơn vị: m/s).
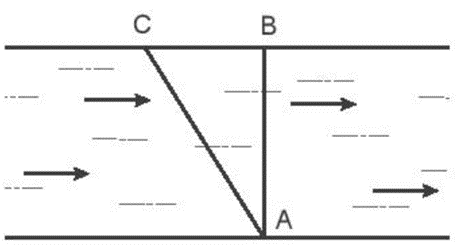
Đáp án đúng là:
Thời gian chuyển động: \(t = \dfrac{s}{v}\)
Định lí Pi-ta-go: \({a^2} = {b^2} + {c^2}\)
Đáp án cần điền là: 1
Một electron chuyển động trong ống đèn hình của một máy thu hình. Nó tăng tốc đều đặn từ vận tốc \({3.10^4}\,\,m/s\) đến vận tốc \({5.10^6}\,\,m/s\) trên một đoạn đường thẳng bằng 2 cm. Hãy tính thời gian electron đi hết quãng đường đó. (Đơn vị: ns, kết quả làm tròn đến hàng đơn vị).
Đáp án đúng là:
Độ dịch chuyển trong chuyển động biến đổi đều: \(d = \dfrac{{{v^2} - {v_0}^2}}{{2a}}\)
\(a = \dfrac{{v - {v_0}}}{t}\)
Đáp án cần điền là: 8
Một vật đang chuyển động thẳng đều với vận tốc 5 m/s. Nếu không có lực nào tác dụng lên nó, sau 3 giây vật đi được quãng đường bao nhiêu mét?
Đáp án đúng là:
Sử dụng công thức: $s = vt$
Đáp án cần điền là: 15
Một xe chuyển động thẳng, vận tốc tăng đều từ $v_{0} = 5m/s$. Sau 4 s quãng đường tăng thêm 44m so với quãng đường đi được trong 2 giây đầu. Gia tốc của xe là bao nhiêu $m/s^{2}$? (Kết quả làm tròn đến hàng phần trăm).
Đáp án đúng là:
Sử dụng công thức: $s = v_{0}t + \dfrac{1}{2}at^{2}$.
Đáp án cần điền là: 5,67
