Một mặt phẳng hoàn toàn được xác định nếu biết các yếu tố nào sau đây?
Đáp án đúng là: C
Đáp án cần chọn là: C
Tất cả các nghiệm của phương trình $\cot\left( {x - 15^{{^\circ}}} \right) - \sqrt{3} = 0$ là:
Đáp án đúng là: B
Phương trình $\left. \cot u = \cot v\Leftrightarrow u = v + k180^{{^\circ}},(k \in {\mathbb{Z}}) \right.$, có $\cot 30^{o} = \sqrt{3}$
Đáp án cần chọn là: B
Trong các hàm số sau, hàm số nào là hàm số chẵn?
Đáp án đúng là: D
Hàm số $y = f(x)$ được gọi là hàm số chẵn nếu $f( - x) = f(x)$ với mọi $x$ thuộc tập xác định.
Đáp án cần chọn là: D
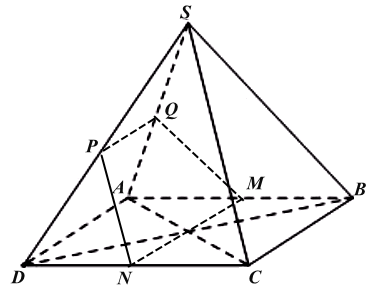
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm các cạnh \(AB\), \(CD\), \(SD\) và \(SA\). Chọn khẳng định sai trong các khẳng định dưới đây:
Đáp án đúng là: B
Sử dụng định nghĩa đường trung bình của tam giác và quy tắc xác định đường thẳng song song với mặt phẳng.
Kiểm tra từng đáp án.
Đáp án cần chọn là: B
Cho dãy số $\left( u_{n} \right)$ được xác định bởi: $\left\{ \begin{array}{l} {u_{1} = 1} \\ {u_{n + 1} = 2u_{n} - 5} \end{array} \right.$. Tính số hạng $u_{3}$.
Đáp án đúng là: C
Thay $n = 2$ vào $u_{n + 1} = 2u_{n} - 5$.
Đáp án cần chọn là: C
Trong các khẳng định sau, khẳng định nào sai?
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho cấp số nhân $\left( u_{n} \right)$ biết $u_{1} = - 2$ và công bội $\text{q} = 3$. Tính số hạng $u_{5}$.
Đáp án đúng là: A
Công thức số hạng tổng quát của cấp số nhân là $u_{n} = u_{1} \cdot q^{n - 1}$.
Đáp án cần chọn là: A
Chọn khẳng định đúng.
Đáp án đúng là: B
Công thức nhân đôi của cos:
$\cos 2a = \cos^{2}a - \sin^{2}a = 2\cos^{2}a - 1 = 1 - 2\sin^{2}a$
Đáp án cần chọn là: B
Cho dãy số $\left( u_{n} \right)$ với $u_{n} = {( - 2)}^{n}$. Số hạng thứ tư của dãy số đã cho là
Đáp án đúng là: C
Thay $n = 4$ vào số hạng tổng quát của dãy số.
Đáp án cần chọn là: C
Góc lượng giác $\dfrac{24\pi}{5}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
Đáp án đúng là: B
Các góc có cùng điểm biểu diễn là các góc sai khác nhau một bội số của $2\pi$.
Góc $\dfrac{24\pi}{5}$ có cùng điểm biểu diễn với góc $\dfrac{4\pi}{5}$.
Đáp án cần chọn là: B
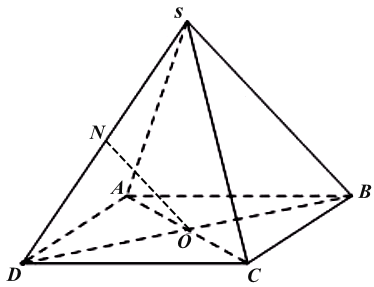
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Hình chiếu song song của điểm O lên $(SAD)$ theo phương của đường thẳng SB là:
Đáp án đúng là: D
Sử dụng tính chất hình chiếu song song:
1. Xác định mặt phẳng chứa O và song song với SB.
2. Tìm giao tuyến của mặt phẳng đó với mặt phẳng (SAD).
3. Tìm điểm cắt của đường thẳng qua O song song với SB với giao tuyến vừa tìm được.
Đáp án cần chọn là: D
Cho dãy số $\left( u_{n} \right)$ có số hạng tổng quát $u_{n} = 1 - \dfrac{n}{n^{2} + 1}$ (với $n \in {\mathbb{N}}^{*}$). Số hạng thứ 10 của dãy số là:
Đáp án đúng là: B
Để tìm số hạng thứ $k$ của một dãy số khi biết công thức số hạng tổng quát $u_{n}$, ta chỉ cần thay $n = k$ vào công thức.
Đáp án cần chọn là: B
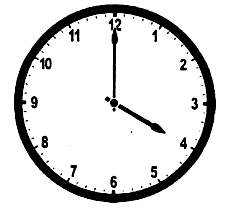
Một chiếc đồng hồ có kim giờ và kim phút được cho như trong hình vẽ sau. Chiều dài kim giờ, kim phút lần lượt bằng 8cm và 10cm. Kiểm tra tính đúng sai của các khẳng định sau
| Đúng | Sai | |
|---|---|---|
| a) Đồng hồ chỉ 6 giờ kim giờ quay được góc bằng $\dfrac{\pi}{3}$. | ||
| b) Đồng hồ chỉ 6 giờ kim giờ quét được một cung có độ dài bằng $\dfrac{8\pi}{3}(~\text{cm})$. | ||
| c) Đồng hồ chỉ 6 giờ 15 phút kim phút quay được góc bằng $\dfrac{9\pi}{2}$ | ||
| d) Đồng hồ chỉ 6 giờ 15 phút kim phút quét được một cung có độ dài bằng $90\pi(~\text{cm})$. |
Đáp án đúng là: Đ; Đ; Đ; S
Tìm số vòng quay của kim phút và kim giờ theo thời gian bài cho từ đó tính góc quay và độ dài cung.
Góc quay = Số vòng quay nhân với $2\pi$ (đơn vị rad)
Độ dài cung = Góc quay nhân với bán kính (đơn vị radian)
Đáp án cần chọn là: Đ; Đ; Đ; S
Cho biểu thức $P = \dfrac{\sin x + 2\sin 2x + \sin 3x}{\cos x + 1}$.
| Đúng | Sai | |
|---|---|---|
| a) Rút gọn P ta được $P = \sin 2x$. | ||
| b) Tồn tại 3 giá trị của $x \in \lbrack 0;2\pi\rbrack$ để $P = 0$. | ||
| c) Điều kiện xác định của biểu thức P là $x \neq - \dfrac{\pi}{2} + k\pi$. | ||
| d) Tại $x = \dfrac{\pi}{4}$ thì $P = 2$. |
Đáp án đúng là: S; S; S; Đ
a) Rút gọn biểu thức lượng giác bằng cách sử dụng các công thức cộng, biến đổi tổng thành tích.
b) Giải phương trình $P = 0$ để tìm số nghiệm trong khoảng cho trước.
c) Tìm điều kiện xác định của biểu thức.
d) Thay giá trị $x$ vào biểu thức đã rút gọn để tính giá trị của P.
Đáp án cần chọn là: S; S; S; Đ
Cho hàm số $y = 2\sin\left( {\dfrac{5\pi}{2} - \dfrac{\pi x}{6}} \right) + 11$.
| Đúng | Sai | |
|---|---|---|
| a) Hàm số có tập xác định là $D = {\mathbb{R}}$. | ||
| b) Hàm số tuần hoàn với chu kì $T = 12\pi$. | ||
| c) Hàm số là hàm số lẻ. | ||
| d) Giá trị lớn nhất của hàm số là 13. |
Đáp án đúng là: Đ; S; S; Đ
a) Tập xác định hàm $\sin x,\cos x$ là $D = {\mathbb{R}}$
b) Hàm số $\sin\left( {ax + b} \right)$ tuần hoàn với chu kì $T = \dfrac{2\pi}{|a|}$
c) Hàm số chẵn nếu $f\left( {- x} \right) = f(x)$
d) Từ $- 1 \leq \sin x \leq 1; - 1 \leq \cos x \leq 1$ tìm GTNN của hàm số.
Đáp án cần chọn là: Đ; S; S; Đ
Các mệnh đề sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Hai đường thẳng chéo nhau thì không có điểm chung. | ||
| b) Hai đường thẳng song song xác định một mặt phẳng. | ||
| c) Hai đường thẳng được gọi là song song nếu chúng không có điểm chung. | ||
| d) Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau. |
Đáp án đúng là: Đ; Đ; S; S
Các định nghĩa và tính chất cơ bản về quan hệ song song trong không gian:
- Hai đường thẳng chéo nhau.
- Hai đường thẳng song song.
Đáp án cần chọn là: Đ; Đ; S; S
Có bao nhiêu giá trị của $x$ trên đoạn $\lbrack - \pi;\pi\rbrack$ để hàm số $y = \cos x$ nhận giá trị bằng $\dfrac{1}{2}$?
Đáp án đúng là:
Giải phương trình lượng giác $\cos x = \dfrac{1}{2}$ trên đoạn $\lbrack - \pi;\pi\rbrack$.
Xác định các giá trị của $x$ trong khoảng đã cho.
Đáp án cần điền là: 2
Cho dãy số $\left( u_{n} \right)$, biết $u_{n} = \left( {2 - a} \right)n + a - 2,\forall n \in {\mathbb{N}}^{\text{*}}$. Có tất cả bao nhiêu số nguyên dương $a$ để dãy số $\left( u_{n} \right)$ là dãy tăng?
Đáp án đúng là:
Tính $u_{n + 1} - u_{n}$
($u_{n}$) là dãy tăng $\left. \Leftrightarrow u_{n + 1} - u_{n} > 0\forall n \in {\mathbb{N}}^{\text{*}} \right.$.
Đáp án cần điền là: 1
Chị An được nhận vào làm việc ở một công ty may với mức lương khởi điểm là 72 triệu đồng một năm, từ năm thứ 2 trở đi công ty sẽ tăng lương cho chị mỗi năm thêm 20 triệu đồng. Hỏi sau 10 năm làm việc cho công ty đó, tổng số tiền lương chị An nhận được là bao nhiêu triệu đồng?
Đáp án đúng là:
Xác định dãy số biểu diễn số tiền lương mỗi năm của chị An.
Tính tổng của dãy số đó sau 10 năm.
Dãy số này là một cấp số cộng. Tổng số tiền lương chị An nhận được sau 10 năm làm việc là tổng của 10 số hạng đầu của cấp số cộng.
Đáp án cần điền là: 1620
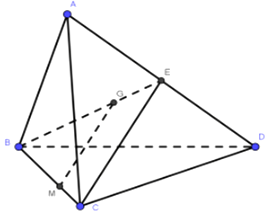
Cho tứ diện ABCD có G là trọng tâm của $\bigtriangleup ABD$ và M là một điểm trên cạnh BC sao cho $MB = x.MC$. Tìm $x$ để đường thẳng MG song song với mặt phẳng $(ACD)$.
Đáp án đúng là:
Sử dụng tính chất trọng tâm: \(G\) nằm trên \(B E\) và \(B G=2 G E\).
Để \(M G \|(A C D)\) thì \(M G \| C E\) (vì \(C E \subset(A C D)\) ).
Dùng định lý Thales trong tam giác \(B C E\) để tìm tỉ số \(\frac{B M}{M C}\).
Đáp án cần điền là: 2
Một bánh xe đạp quay được 25 vòng trong 10 giây. Tính độ dài quãng đường mà người đi xe thực hiện được trong 2,35 phút, biết rằng bán kính bánh xe bằng 340mm. (Tính theo đơn vị mét, kết quả được làm tròn đến hàng đơn vị).
Đáp án đúng là:
Tính số vòng mà bánh xe đi được trong 2,35 phút là $x$ vòng
Quãng đường mà người đi xe đạp đi là $S = x.2\pi R$
Đáp án cần điền là: 753
Aladin nhặt được cây đèn thần, chàng miết tay vào cây đèn và gọi Thần đèn ra. Thần đèn cho chàng 3 điều ước. Aladin ước 2 điều đầu tiên tùy thích, nhưng điều ước thứ 3 của chàng là: "Ước gì ngày mai tôi lại nhặt được cây đèn và Thần cho tôi số điều ước gấp đôi số điều ước ngày hôm nay". Thần đèn chấp thuận và mỗi ngày Aladin đều thực hiện theo quy tắc như trên: ước hết các điều đầu tiên và luôn chừa lại điều ước cuối cùng để kéo dài thỏa thuận với thần đèn cho ngày hôm sau. Hỏi sau 10 ngày gặp Thần đèn, Aladin ước tất cả bao nhiêu điều ước
Đáp án đúng là:
Đưa bài toán về cấp số nhân $u_{n} = u_{1}.q^{n - 1}$u
Tổng n số hạng cấp số nhân $S_{n} = u_{1}.\dfrac{q^{n} - 1}{q - 1}$
Đáp án cần điền là: 3069