Câu hỏi số 1:

 

Cho hàm số y=x^{4}-2(m+1)x^{2}+2m (1) (m là tham số).

1. Khảo sát và vẽ đồ thị (C) của hàm số (1) khi m=1.

2. Tìm m để đồ thị hàm số (1) có ba điểm cực trị tạo thành một tam giác có trọng tâm là điểm G(0;2).

Câu hỏi: 66969

Câu hỏi số 2:

 

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=xln^{2}x trên đoạn [e^{-3};e]

Câu hỏi: 66970

Câu hỏi số 3:

 

1. Giải phương trình: \frac{1}{2}log_{\sqrt{2}}(x+3)+\frac{1}{2}log_{2}(x-1)^{2}=log_{2}(4x)

2. Cho phương trình:

      (\sqrt{5}+1)^{x}+m(5-1)^{x}=2^{x} (với m là tham số)

Tìm m để phương trình có nghiệm thuộc đoạn [0,1]

Câu hỏi: 66971

Câu hỏi số 4:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông  tại A, AB=a 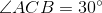\angle ACB=30^{\circ}. Mặt phẳng (B'AC) tạo với mặt phẳng (ABC) một góc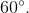 60^{\circ}.

  1. Tính thể tích của khối lăng trụ ABC.A'B'C'.

  2. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp A'ABC.

  3 Tính khoảng cách giữa hai đường thẳng B'C và AB.

Câu hỏi: 66972

Câu hỏi số 5:

 Giải hệ phương trình:

\left\{\begin{matrix} x^{2}-y^{2}+5x-3y+4=0 & \\ log_{12}(x-1)+log_{12}(y-3)=1 & \end{matrix}\right.

Câu hỏi: 66973
Quy định - Hướng dẫn làm đề thi thử
  • 1. Tất cả các đề thi thử trên Tuyển sinh 247 đều có hướng dẫn giải chi tiết
  • 2. Bảng xếp hạng chỉ áp dụng cho những thành viên thi lần 1, không tính thi lại
  • 3. Bất cứ khi nào bạn cũng có thể làm đề thi thử đã thi nhưng điểm sẽ không được tính vào điểm thành tích cũng như bảng xếp hạng