Đề thi vào lớp 10 môn Tóan chuyên trường PT năng khiếu năm 2011

Thời gian thi : 120 phút - Số câu hỏi : 12 câu - Số lượt thi : 787

Click vào đề thi  

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Cho phương trình bậc hai x2 – (m + 3)x + m2 = 0, trong đó m là tham số sao cho phương trình có hai nghiệm phân biệt x1, x2. 

Câu 1: Khi m = 1, chứng minh rằng ta có hệ thức \sqrt[8]{x_{1}}+\sqrt[8]{x_{2}}=\sqrt{2+\sqrt{2+\sqrt{6}}}

Câu 2: Tìm tất cả các giá trị của m sao cho √x1 + √x2 = √5.

Câu 3: Xét đa thức P(x) = x3 + ax2 + bx. Tìm tất cả các cặp số (a, b) sao cho ta có hệ thức P(x1) = P(x2) với mọi giá trị của tham số m.

Câu 4: Cho a, b  là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 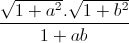\frac{\sqrt{1+a^{2}}.\sqrt{1+b^{2}}}{1+ab}

Câu 5: Cho x, y, z là các số thực thỏa mãn điều kiện |x| ≤ 1, |y| ≤ 1, |z| ≤ 1.

Chứng minh rằng ta có bất đẳng thức 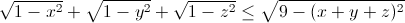\sqrt{1-x^{2}}+\sqrt{1-y^{2}}+\sqrt{1-z^{2}}\leq \sqrt{9-(x+y+z)^{2}}

Cho tam giác nhọn ABC có AB = b, AC = c. M là một điểm thay đổi trên cạnh AB. Đường tròn ngoại tiếp tam giác  BMC  cắt các cạnh AC tại N.

Câu 6: Chứng minh tam giác AMN đồng dạng với tam giác ACB. Tính tỷ số 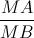\frac{MA}{MB} để diện tích tam giác AMN bằng một nửa tam giác ACB.

Câu 7: Gọi I là tâm đường tròn ngoại tiếp tam giác AMN. Chứng minh I luôn thuộc một đường thẳng cố định.

Câu 8: Gọi J là tâm đường tròn ngoại tiếp tam giác BMC. Chứng minh rằng độ dài IJ không đổi.

Cho a, b , c là các số nguyên sao cho 2a + b, 2b + c, 2c + a đều là các số chính phương (*).

Câu 9: Biết rằng có ít nhất một trong ba số chính phương nói trên chia hết cho 3. Chứng minh rằng tích (a – b)(b – c)(c – a) chia hết cho 27.

Câu 10: Tồn tại hay không các số nguyên a, b, c thỏa mãn điều kiện (*) sao cho (a – b)(b – c)(c – a) không chia hết cho 27. 

Cho hình chữ nhật ABCD có AB = 3; BC = 4.

Câu 11: Chứng minh rằng từ 7 điểm bất kỳ nằm trong hình chữ nhật ABCD luôn tìm được hai điểm mà khoảng cách giữa chúng lớn hơn √5.

Câu 12: Chứng minh rằng khẳng định ở câu a) vẫn còn đúng với 6 điểm bất kỳ nằm trong hình chữ nhật ABCD.

Bạn có đủ giỏi để vượt qua

lamlinh35 Lâm Linh
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 Lâm Linh 0 1 0% 2.95
2 Lương Công Quỳnh 2 12 17% 3.72
3 Nguyen Van Chuong 2 11 18% 0.48
4 HỒ LỮ TÚ 12 12 100% 0.73
5 Nguyen Dinh Hao 2001 7 12 58% 20.75
6 Ngay Tho Co Be 1 9 11% 1.52
7 Nguyen Thanh Lan 6 12 50% 1.75
8 Ba Tuan 1 4 25% 2.13
9 Nguyễn Quang Tùng 2 12 17% 1.27
10 Diệu Hiền 9 12 75% 0.73
11 Nguyễn Chấn Phong 0 0 0% 0.3
12 ʚɞKatori The Virgoʚɞ 0 4 0% 0.73
13 Con Nhà Nghèo 2 12 17% 0.2
14 Baokute Nhontho 0 12 0% 1.72

Cùng tham gia trao đổi với bạn bè!

Lớp 9