Đề luyện Số phức

Đề luyện Số phức - Đề số 1

Thời gian thi : 120 phút - Số câu hỏi : 10 câu - Số lượt thi : 281

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Tìm số phức z thỏa mãn 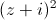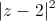$(z+i)^{2}$ + $\left|z-2\right|^{2}$ =2 $(\bar{z}-3i)^{2}$ .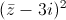

Câu 2: Tìm các số phức z, w thỏa mãn z + w = 4 - i và z³+ w³= 7 + 28i.

Câu 3: Tìm số phức z thỏa mãn 2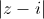 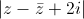$\left|z-i\right|$ = $\left|z-\bar{z}+2i\right|$ và (2-z)(i+ 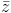$\bar{z}$ ) là số thực.

Câu 4: Tìm số thực m để phương trình sau có nghiệm z=i: z³-(3+i)z²+(3+4i)z+1-mi=0 Với giá trị m tìm được, hãy giải phương trình đã cho.

Câu 5: Cho số phức z thỏa mãn 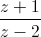$\frac{z+1}{z-2}$ = z + 3. Tính môđun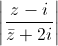 $\left|\frac{z-i}{\bar{z}+2i}\right|$

Câu 6: Giả sử z₁,z₂ là các số phức thỏa mãn z₁²+z₂²= z_zz₂ Tính 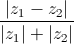$\frac{|z_{1}-z_{2}|}{|z_{1}|+|z_{2}|}$

Câu 7: Tìm số nguyên dương n nhỏ nhất sao cho z₁= 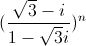$(\frac{\sqrt{3}-i}{1-\sqrt{3}i})^{n}$ là số thực và z₂= 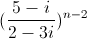$(\frac{5-i}{2-3i})^{n-2}$ là số ảo.

Câu 8: Trong mặt phẳng tọa độ, giả sử điểm A biểu diễn nghiệm z₁ của phương trình z²-2z+5=0 và điểm B biểu diễn số phức z₂=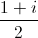 $\frac{1+i}{2}$ z₁. Tính diện tích tam giác OAB (O là gốc tọa độ).

Câu 9: Cho số phức z thỏa mãn 2|z|+√3iz=4-z. Tính z²⁰¹²+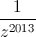 $\frac{1}{z^{2013}}$

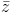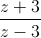Câu 10: Tìm số phức z thỏa mãn |1 - 2z| = |i - 2 $\bar{z}$ | và $\frac{z+3}{z-3}$ có một acgumen bằng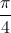 $\frac{\pi}{4}$

Bạn có đủ giỏi để vượt qua

Huỳnh Trúc

Xếp hạng

Thành viên

Đúng

Làm

Đạt

Phút

1	Huỳnh Trúc	1	2	50%	2.95
2	Hoàng Hiệp	0	0	0%	0.18
3	trần thanh thùy	0	1	0%	0.62
4	Meoden Mapmap	3	10	30%	19.25
5	leminhthang	0	2	0%	0.13
6	vothibichphuong	0	2	0%	0.1
7	lê thị nguyệt	1	10	10%	0.45

Cùng tham gia trao đổi với bạn bè!

Lớp 12