Đề thi thử đại học môn Toán đề số 11

Đề thi thử đại học môn Toán đề số 11

Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 192

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y = x³- 3(m-3)x²+3(m² – 3m + 5)x + 1, m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m=1 (HS tự làm). b) Tìm m để hàm số đã cho đạt cực đại, cực tiểu tại x_1;x_{2 thỏa mãn}|x₁₊x₂ - x₁x_{2|< 7.}

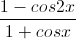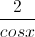Câu 2: Giải phương trình $\frac{1-cos2x}{1+cosx}$ = 2 -tan²x - $\frac{2}{cosx}$ .

Câu 3: Chọn phát biểu sai khi nói về sự phóng xạ:

Câu 4: Giải hệ phương trình: 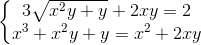$\left\{\begin{matrix}3\sqrt{x^{2}y+y} +2xy=2\\x^{3}+x^{2}y+y=x^{2}+2xy\end{matrix}\right.$

Câu 5: Tính tích phân: I=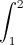 $\int_{1}^{2}$ xln(3x -x² )dx.

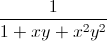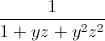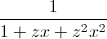
Câu 6: Cho các số thực không âm x, y, z thỏa mãn x + y +z =3. Tìm giá trị nhỏ nhất của biếu thức P = $\frac{1}{1+xy+x^{2}y^{2}}$ + $\frac{1}{1+yz+y^{2}z^{2}}$ + $\frac{1}{1+zx+z^{2}x^{2}}$

Câu 7: Trong mặt phẳng với hệ trục Oxy, cho hình chữ nhật ABCD có BC: 4x – 3y – 3 = 0, AD: 4x -3y -17 = 0, giao điểm của hai đường chéo nằm trên đường thẳng d: x+ y + 1 =0. Viết phương trình cạnh AB biết rằng BC = 3CD.

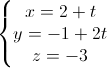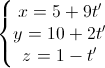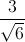Câu 8: Trong không gian với hệ tọa độ Oxyz, cho (P) : x –y +2z +6 =0, ∆₁: $\left\{\begin{matrix}x=2+t\\y=-1+2t\\z=-3\end{matrix}\right.$ , ∆₂: $\left\{\begin{matrix}x=5+9t'\\y=10+2t'\\z=1-t'\end{matrix}\right.$ Viết phương trình đường thẳng ∆ cắt hai đường thẳng ∆₁ , ∆₂ sao cho ∆ // (P) và khoảng cách từ ∆ đến (P) bằng $\frac{3}{\sqrt{6}}$ .

Câu 9: Cho số phức z thỏa mãn z² – 6z + 13 =0. Tính |z + 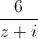$\frac{6}{z+i}$ |

Câu 10: Trong mặt phẳng với hệ trục Oxy, cho ba đường thẳng d₁ : x -2 =0, d₂ : x + y -4 =0, d₃ : 3x –y -2 =0.Tìm tọa độ các đỉnh của hình thoi ABCD biết 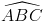$\widehat{ABC}$ = 120⁰, các đỉnh B và D thuộc d₁, C thuộc d₃, A thuộc d₂.

Câu 11: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : 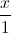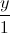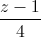$\frac{x}{1}$ = $\frac{y}{1}$ = $\frac{z-1}{4}$ và M (0;3;-2). Viết phương trình (P) đi qua M, song song với đường thẳng ∆ và cách đường thẳng ∆ một khoảng bằng 3.

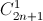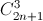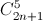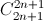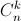Câu 12: Cho khai triển (2 – $\sqrt[3]{3}$ x)²ⁿ = a₀ + a₁x + ….+ a_2nx²ⁿ.Tính hệ số a₉, biết rằng số tự nhiên n thỏa mãn hệ thức $C_{2n+1}^{1}$ + $C_{2n+1}^{3}$ + $C_{2n+1}^{5}$ +...+ $C_{2n+1}^{2n+1}$ = 4096 ( $C_{n}^{k}$ là số tổ hợp chập k của n phần tử ).

Cùng tham gia trao đổi với bạn bè!

Lớp 12