Đề thi thử đại học môn Toán đề số 13
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 208
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x4 -2mx2 + 2m -1, với m là tham số. (a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m =3 (HS tự làm). (b) Tìm m để đồ thị hàm số đã cho có 3 điểm cực trị lập thành một tam giác vuông.
Câu 2: Giải phương trình: sin4x + 2cos2x + 4(sinx + cosx) = 1 + cos4x.
Câu 3: Giải phương trình: log2(17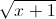 + 34
+ 34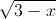 ) + x = 2 + log2( 4x + 4).
) + x = 2 + log2( 4x + 4).
Câu 4: Tính tích phân I= 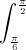 sin2xln(sinx)dx
sin2xln(sinx)dx
Câu 5: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật , AB = a√3, AA’ =AC = 2a√3. Hình chiếu của B xuống (A’B’C’D’) trùng với trung điểm của B’D’. Tính thể tích khối hộp ABCD.A’B’C’D’ và góc giữa hai đường thẳng AC và BB’.
Câu 6: Cho các số thực x,y thỏa mãn 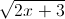 +
+ 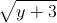 = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =
= 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 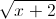 +
+ 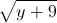
Câu 7: Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có đường cao CH có phương trình x + y -5 =0, trung tuyến AM có phương trình 2x – y -4 =0. Tìm tọa độ 3 đỉnh của tam giác đã cho biết rằng E(2;3) là trung điểm của AC.
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;3), đường thẳng d : 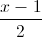 =
= 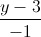 =
= 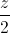 và mặt phẳng (P) : 3x –y + z -3 =0. Tìm tọa độ điểm B thuộc mặt phẳng (P) sao cho đường thẳng AB vuông góc và cắt đường thẳng d.
và mặt phẳng (P) : 3x –y + z -3 =0. Tìm tọa độ điểm B thuộc mặt phẳng (P) sao cho đường thẳng AB vuông góc và cắt đường thẳng d.
Câu 9: Khai triển và rút gọn biểu thức 1 – x + 2(1 – x)2 +…+n( 1 –x)n thu được đa thức P(x) = a0 + a1x + …+anxn. Tìm hệ số a8 biết rằng n là số nguyên dương thỏa mãn 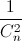 +
+ 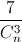 =
= 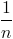 . (
. ( 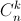 là số tổ hợp chập k của n phần tử).
là số tổ hợp chập k của n phần tử).
Câu 10: Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có đường cao BH: 7x – y -19 = 0, phân giác trong AD: x + 2y -2 =0, M (13;8) thuộc tia đối của tia AB thỏa mãn AC = 3AM. Tìm tọa độ ba đỉnh của tam giác ABC.
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho (S): x2 + y2 + z2 – 2x + 4y -6z -11 =0, (P): 2x + 2y –z -7 =0. Chứng minh mặt cầu (S) cắt (P) theo giao tuyến là một đường tròn (C). Viết phương trình mặt cầu (S’) đi qua A (6; -1 ;4) và chứa đường tròn ( C ).
Câu 12: Tìm số phức z sao cho |z -1| = |z -3| và một acgumen của z -3 bằng một acgumen của z + 3 cộng với 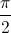 .
.