Đề thi thử đại học môn toán đề số 18
Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 200
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = 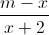 có đồ thị là (Hm) với m là tham số thực. 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (Hm) của hàm số đã cho khi m = 1. 2. Tìm m để đường thẳng d: 2x + 2y - 1 = 0 cắt (Hm) tại hai điểm cùng với gốc tọa độ tạo thành một tam giác có diện tích S =
có đồ thị là (Hm) với m là tham số thực. 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số (Hm) của hàm số đã cho khi m = 1. 2. Tìm m để đường thẳng d: 2x + 2y - 1 = 0 cắt (Hm) tại hai điểm cùng với gốc tọa độ tạo thành một tam giác có diện tích S = 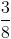
Câu 2: Giải phương trình 1 + (cot x)sin3x + (cos x + sin x) cos2 x = cos x + sin x
Câu 3: Tính tích phân I = 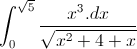
Câu 4: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M,N lần lượt la nằm trên hai cạnh B'C' và DD' sao cho C'M = DN = x.Mặt phẳng (MAD') cắt BB' tại P. Chứng minh rằng CM ⊥ BN và tìm x theo a để thể tích khối lập phương đã cho gấp 3 lần thể tích khối đa diện MPB'.D' AA'
Câu 5: Cho các số thực dương x, y, z thỏa mãn điều kiện x2 + y2 + z2 + 2xy = 3(x + y + z). Tìm giá chị nhỏ nhất của biểu thức P = x + y + z + 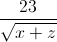 +
+ 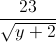
Câu 6: Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông cân tại B, đường thẳng AB đi qua điểm M(-3;-1), điểm B nằm trên đường thẳng ∆: x - 4y = 0, đường thẳng AC có phương trình 2x - y - 5 = 0. Tìm tọa độ các đỉnh của ABC biết rằng đỉnh B có hoành độ là một số nguyên
Câu 7: Trong không gian với hệ tọa độ Oxyz,cho ba mặt phẳng (P): 2x - y + z + 1 = 0, (Q): x - y + 2z + 3 = 0,(R): x + 2y - 4z + 1 = 0và đường thẳng ∆ : 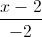 =
= 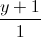 =
= 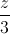 . Viết phương trình đường thẳng d vuông góc với (R), cắt hai đường thẳng ∆ và giao tuyến của hai mặt phẳng (P) và (Q).
. Viết phương trình đường thẳng d vuông góc với (R), cắt hai đường thẳng ∆ và giao tuyến của hai mặt phẳng (P) và (Q).
Câu 8: Tìm số phức Z thỏa mãn |z - i| = √2 và (z - 1)(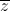 + i) là số thực
+ i) là số thực
Câu 9: Trong mặt phẳng với hệ trục Oxy, cho đường thẳng ∆: 2x -5y + 16 = 0 và đường tròn (C) : x2 + y2 – 2y – 4 = 0. Tìm điểm M nằm trên đường thẳng ∆ sao cho từ đó kẻ được hai tiếp tuyến đến đường tròn (C) và độ dài đoạn thẳng nối hai tiếp điểm bằng √10
Câu 10: Trong không gian với hệ tọa độ Oxyz,cho hai mặt phẳng 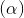 : 3x - y + z -2 = 0,
: 3x - y + z -2 = 0, 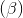 : x + 4y - 5 = 0. Viết phương trình mặt phẳng (P) chứa giao tuyến của hai mặt phẳng đã cho và vuông góc với
: x + 4y - 5 = 0. Viết phương trình mặt phẳng (P) chứa giao tuyến của hai mặt phẳng đã cho và vuông góc với 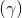 : 2x - z + 7 = 0
: 2x - z + 7 = 0
Câu 11: Giải hệ phương trình 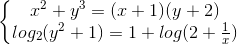 (x; y ∈ R)
(x; y ∈ R)