Đề thi thử Đại học môn Toán đề số 22
Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 191
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y =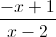 
. (1). Khảo sát sự biến thiên và vẽ đồ thị hàm số. (2). Tìm trên đồ thị các điểm A, B sao cho độ dài AB = 4 và đường thẳng AB vuông góc với đường thẳng y = x
Câu 2: Giải phương trình: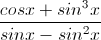 
= 1 + sinx + cotx
Câu 3: Giải hệ phương trình: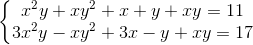 
(x, y ∈ 
)
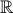Câu 4: Tính diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = (x - 1)![\sqrt[3]{3-4x}](http://images.tuyensinh247.com/picture/learning/exam/2013/1113/2331_702_1.gif)
và trục hoành
Câu 5: Cho x, y, z là các số thực không âm phân biệt. Chứng minh rằng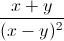 
+ 
+ 
≥ 
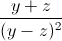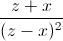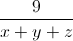
Câu 6: Trong mặt phẳng với hệ trục Oxy, cho đường thẳng d: x - 2y + 2 = 0 và đường tròn (C): (x – 1)2 + (y – 1)2= 10. Lập phương trình đường thẳng ∆ tiếp xúc với đường tròn (C) và tạo với đường thẳng d một góc bằng 450.
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho điểm A (5 ; -7 ; 1) và đường thẳng ∆: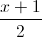 
= 
= 
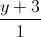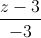. Viết phương trình đường thẳng d đi qua A, cắt và tạo với đường thẳng ∆ một góc 600
Câu 8: Tìm tập hợp điểm trong mặt phẳng tọa độ biểu diễn số phức w = 2z + 3 - i, biết rằng |2z + i|2 ≤ 3z.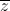
+ 1
Câu 9: Trong mặt phẳng với hệ trục Oxy, cho tam giác nội tiếp đường tròn (C): x2 + y2 – 2x – 4y – 8 = 0. Biết rằng đỉnh B thuộc tia Ox, đường cao vẽ từ A nằm trên đường thẳng d : 5x + y = 0. Tìm tọa độ A, B, C biết rằng điểm A có tung độ là một số nguyên
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ có phương trình ∆: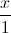 
= 
= 
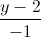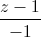. Viết phương trình mặt phẳng (P) chưa đường thẳng ∆, biết rằng (P) tạo với các trục Oy, Oz những góc bằng nhau.
Câu 11: Giải hệ phương trình: 
