Đề thi thử đại học môn Toán đề số 28

Câu 1: Giải phương trình:  cos² (x + 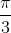) + sin² (x + 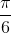) = 2sinx - 

Câu 2: Giải bất phương trình:  log₇ (x² + x + 1) ≥ log₂ x

Câu 3: Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh bằng a, cạnh SA vuông góc với mặt phẳng đáy, góc phẳng nhị diện cạnh SC bằng 120⁰  . Tính thể tích của hình chóp.

Câu 4: Tính tích phân:  I = 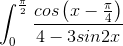dx

Câu 5: Giả sử x, y, z là các số thực thoả mãn x + y + z = 6. Chứng minh rằng: 8^x  + 8^y  + 8^z 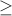  4^x+1 + 4^y+1 + 4^z+1  Dấu đẳng thức xảy ra khi nào?

Câu 6: Trong mặt phẳng Oxy, cho hai đường thẳng có phương trình: d₁ : x + y + 1 = 0 d₂ : 2x - y - 1 = 0 Lập phương trình đường thẳng qua điểm M( 1 ; -1 ) cắt d₁ , d₂  tương ứng tại A và B sao cho: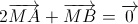

Câu 7: Trong không gian cho mặt phẳng Oxyz, cho mặt phẳng (P): x + 2y - 2z + 1 = 0 và hai điểm A(1; 7; -1), B(4; 2; 0). Lập phương trình đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mặt phẳng (P)

Câu 8: Tìm số phức z thỏa mãn đồng thời hai điều kiện sau: |z + 1 - 2i| = |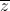 + 3 +4i| và  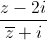là một số ảo

Câu 9: Trong mặt phẳng Oxy, cho đường tròn có phương trình (C): x² + y² – 2x + 1 = 0 và  điểm M(4 ; 3). Chứng tỏ rằng qua M có hai tiếp tuyến với (C) và giả sử A, B là hai điểm tiếp xúc. Lập phương trình đường thẳng đi qua A, B.

Câu 10: Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho hai mặt phẳng (P) có phương trình: 2x - y - 2z - 12 = 0 và hai điểm A(2 ; 1 ; 4), B(1 ; 1 ; 3). Tìm tập hợp các điểm M trên (P) sao cho diện tích của tam giác MAB có giá trị nhỏ nhất.