Đề thi thử đại học môn Toán đề số 29
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 250
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số y = x3 + 2mx2 + (m+3)x+4 (Cm). 1. Khảo sát hàm số khi m = 1. 2. Đường thẳng (d) có phương trình y = x + 4 và điểm M(1 ; 3). Tìm các giá trị của tham số m sao cho (d) cắt (Cm) tại 3 điểm A( 0 ; 4 ), B, C sao cho tam giác MBC có diện tích bằng 8√2.
Câu 2: Giải hệ phương trình: 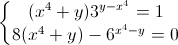
Câu 3: Giải phương trình sau: 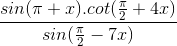 = 1
= 1
Câu 4: Tính tích phân: I = 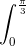
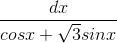
Câu 5: Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, khoảng cách từ tâm I của tam giác ABC đến mặt phẳng (A’BC) bằng 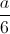 . Tính thể tích của hình lăng trụ ABC.A’B’C’ theo a.
. Tính thể tích của hình lăng trụ ABC.A’B’C’ theo a.
Câu 6: Xác định m để bất phương trình sau nghiệm đúng ∀x∈ R: (6 + 2√7)x + (2 – m)(3 - √7)x – ( m + 1)2x ≥ 0.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, giao điểm I của AC và BD thuộc đường thẳng d: x – y – 3 = 0 có hoành độ x1 = , trung điểm H của AB là giao điểm của (d) và trục Ox. Tìm tọa độ các đỉnh của hình chữ nhật.
, trung điểm H của AB là giao điểm của (d) và trục Ox. Tìm tọa độ các đỉnh của hình chữ nhật.
Câu 8: Trong không gian Oxyz cho mặt phẳng (P): x + y – 2z + 3 = 0, điểm A(1;1;-2) và đường thẳng ∆ là giao tuyến của hai mặt phẳng x – 2y + 7 = 0 và 4y – z – 12 = 0. Tìm phương trình đường thẳng d qua A cắt đường thẳng ∆ và song song với mặt phẳng (P).
Câu 9: Cho x , y là hai số không âm thỏa mãn x + y = 2. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : H = 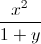 +
+ 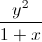
Câu 10: Giải bất phương trình sau: logx+1( 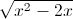 - 1) > 1
- 1) > 1
Câu 11: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức hàm số: A = 8cos3x + 9sin2x – 8sin3x
Câu 12: Cho z là số phức thỏa mãn ( z + 2)(1 + 2i) = 5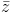 . Xác định phần ảo của số phức w = ( z + 2i)2001
. Xác định phần ảo của số phức w = ( z + 2i)2001
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
6 | 7 | 86% | 14.88 |
| 2 |
|
4 | 9 | 44% | 23.77 |
| 3 |
|
2 | 9 | 22% | 0.3 |