Đề thi thử Đại học môn Toán đề số 35
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 261
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số: 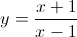 có đồ thị (C). 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. 2. Tìm trên (C) những điểm M sao cho tiếp tuyến tại M lập với hai đường tiệm cận một tam giác có chu vi bé nhất.
có đồ thị (C). 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. 2. Tìm trên (C) những điểm M sao cho tiếp tuyến tại M lập với hai đường tiệm cận một tam giác có chu vi bé nhất.
Câu 2: Giải hệ phương trình:
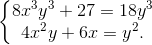
Câu 3: Giải phương trình: (tanx + 7)tanx + (cotx + 7)cotx + 14 = 0.
Câu 4: Tính diện tích miền phẳng D: 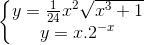
Câu 5: Cho tứ diện ABCD có AB = x, các cạnh còn lại bằng nhau và bằng 1. Xác định x sao cho thể tích của tứ diện đã cho đạt giá trị lớn nhất.
Câu 6: Cho x, y, z >0 và x + y + z = 1. Chứng minh rằng: 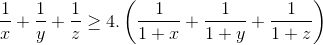
Câu 7: Trong mặt phẳng Oxy cho điểm A(2; -3), B(3; -2), ∆ABC có diện tích bằng  , trọng tâm G của ∆ABC thuộc đường thẳng d: 3x - y -8 = 0. Tìm bán kính đường tròn nội tiếp ∆ABC.
, trọng tâm G của ∆ABC thuộc đường thẳng d: 3x - y -8 = 0. Tìm bán kính đường tròn nội tiếp ∆ABC.
Câu 8: Cho M(1; 2; 1).Viết phương trình mặt phẳng (P) đi qua M cắt các tia Ox, Oy, Oz tại các điểm A, B, C khác 0 sao cho tứ diện OABC có thể tích nhỏ nhất.
Câu 9: Giả sử: P(x) = (2x + 1)13 = a0x13 + a1x12 + …+ a13. Hãy tìm hệ số có giá trị lớn nhất của đa thức P(x).
Câu 10: Trong không gian Oxyz cho A(3; 1; 1) B(7; 3; 9) C(2; 2; 2) và mặt phẳng (P): x + y + z + 3 = 0. Tìm M thuộc (P) sao cho 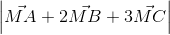 nhỏ nhất.
nhỏ nhất.
Câu 11: Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC= c. Gọi R là bán kính của mặt cầu ngoại tiếp hình chóp đã cho. Chứng minh rằng: R ≥ 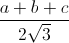
Câu 12: Giải hệ phương trình: 
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
|
4 | 9 | 44% | 56.52 |
| 2 |
|
2 | 12 | 17% | 0.63 |