Đề thi thử Đại học môn Toán đề số 37
Thời gian thi : 180 phút - Số câu hỏi : 12 câu - Số lượt thi : 278
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số: y = 
x3 – mx2 + (5m – 4)x + 2 (Cm). (1). Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 0.(HS tự làm) (2). Tìm m để hàm số có cực đại, cực tiểu và đường thẳng đi qua các điểm cực trị của đồ thị hàm số song song với đường thẳng (d): 8x + 3y + 9 = 0.
Câu 2: Giải phương trình: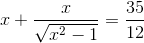 
Câu 3: Giải phương trình: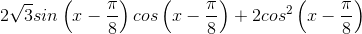 
= ![\sqrt{3}+4\left [ sin^{2}x+cos\left ( \frac{\pi}{3}-x \right )cos\left ( \frac{\pi}{3}+x \right ) \right ].](http://images.tuyensinh247.com/picture/learning/exam/2013/1022/5873_des_1.gif)
Câu 4: Tính tích phân: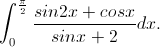 
Câu 5: Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). AB = a, BC = a, góc giữa cạnh bên SB và mp(ABC) bằng 600. M là trung điểm của cạnh AB. Tính khoảng cách từ B đến (SMC).
Câu 6: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: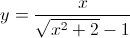 
Câu 7: Cho đường thẳng d: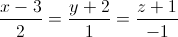 
và mặt phẳng (P) có phương trình: x+ y+ z +2=0. VIết phương trình đường thẳng ∆ thỏa mãn ∆ ⊥ d, (∆)⊂(P) và d(M, ∆) = √42 (M là giao điểm của d và P).
Câu 8: Cho hai điểm A(3; 2) và B(4; 0). Viết phương trình đường thẳng d đi qua A và cắt cạnh OB tại M sao cho tỉ số diện tích hai tam giác AOM và ABM bằng 3.
Câu 9: Tìm phần thực và phần ảo của số phức sau: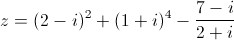 
Câu 10: Trong không gian Oxyz cho 3 đường thẳng: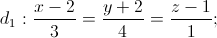 
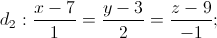
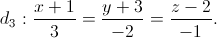Lập phương trình đường thẳng ∆ cắt d1; d2 và song song với d3.
Câu 11: Trong các số phức z = x + yi thỏa mãn điều kiện |z – 2 – 4i| = √5, hãy tìm số phức z có môđun nhỏ nhất, lớn nhất.
Câu 12: Một bàn có hai dãy ghế đối diện nhau, mỗi dãy gồm 4 ghế. Hỏi có bao nhiêu cách xếp chỗ ngồi cho 4 học sinh nam và 4 học sinh nữ sao cho hai học sinh ngồi đối diện nhau phải khác giới tính?
