Đề thi thử đại học môn toán đề số 39

Đề thi thử đại học môn toán đề số 39

Thời gian thi : 180 phút - Số câu hỏi : 9 câu - Số lượt thi : 232

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y = 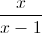$\frac{x}{x-1}$ (C). 1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 2. Viết phương trình tiếp tuyến d của (C) sao cho d va hai tiệm cận của (C) cắt nhau tạo thành một tam giác vuông cân.

Câu 2: Cho tứ diện ABCD có AB = x, các cạnh còn lại bàng nhau và bằng 1. Xác định x sao cho thể tích tứ diện đã cho đạt giá trị lớn nhất.

Câu 3: Cho a, b là các số dương thỏa mãn: ab + a + b = 3. Chứng minh: 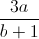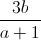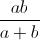$\frac{3a}{b+1}$ + $\frac{3b}{a+1}$ + $\frac{ab}{a+b}$ ≤ a² + b² + $\frac{3}{2}$ .

Câu 4: Chứng minh với mọi n nguyên dương luôn có n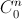 $C_{0}^{n}$ - ( n -1 ) 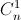$C_{n}^{1}$ + ... + ( -1 )^{n – 2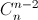} + $C_{n}^{n-2}$ + ( -1 )^{n – 1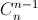} $C_{n}^{n-1}$ = 0

Câu 5: Cho a, b, c là các số dương. Chứng minh bất đẳng thức 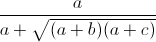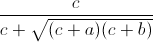$\frac{a}{a+\sqrt{(a+b)(a+c)}}$ + $\frac{b}{b+\sqrt{(b+c)(b+a)}}$ + $\frac{c}{c+\sqrt{(c+a)(c+b)}}$ ≤ 1.

Câu 6: Trong mặt phẳng Oxy cho hai điểm A(2; 1) lấy điểm B thuộc trục OX có hoành độ x ≥ 0 và điểm C thuộc Oy có trung độ y ≥ 0 sao cho ∆ ABC vuông tại A. Tìm B, C sao cho diện tích ∆ ABC lớn nhất.

Câu 7: Giải bất phương trình: 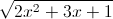$log_{\frac{1}{2}}$ $\sqrt{2x^{2}+3x+1}$ + $\frac{1}{2}$ log₂ (x + 1)² ≥ $\frac{1}{2}$ .

Câu 8: Giải hệ phương trình: 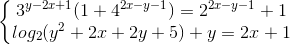$\left\{\begin{matrix} 3^{y-2x+1}(1+4^{2x-y-1})=2^{2x-y-1}+1\\log_{2}(y^{2}+2x+2y+5)+y=2x+1 \end{matrix}\right.$

Câu 9: Cho lăng trụ đứng ABC.A₁B₁C₁ có ABC là tam giác vuông AB = AC = a, AA₁ = a√2. Gọi M, N lần lượt là trung điểm của đoạn AA₁ và BC₁ . Chứng minh MN là đường vuông góc chung của các đường thẳng AA₁ và BC₁.Tính $V_{MA_{1}BC_{1}}$ .

Cùng tham gia trao đổi với bạn bè!

Lớp 12