Đề thi thử đại học môn toán đề số 40
Thời gian thi : 180 phút - Số câu hỏi : 13 câu - Số lượt thi : 251
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số: y = 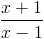 .
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Tính giá trị nhỏ nhất của m sao cho trên đồ thị của hàm số tồn tại cặp điểm có tiếp tuyến song song với nhau và khoảng cách giữa cặp điểm này bằng m. Với giá trị nhỏ nhất của m tìm được, hãy chỉ ra cặp điểm đó.
.
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2. Tính giá trị nhỏ nhất của m sao cho trên đồ thị của hàm số tồn tại cặp điểm có tiếp tuyến song song với nhau và khoảng cách giữa cặp điểm này bằng m. Với giá trị nhỏ nhất của m tìm được, hãy chỉ ra cặp điểm đó.
Câu 2: Cho a, b, c là các số dương thỏa mãn a3 + b3 = c3 Chứng minh bất đẳng thức: a2 + b2 - c2 > 6(c –a)(c – b)
Câu 3: Giải phương trình: sin2 x +  sin2 3x = sinx.sin2 3x.
sin2 3x = sinx.sin2 3x.
Câu 4: Tìm thể tích khối tròn xoay do D quay quanh Ox: D: 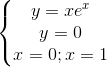
Câu 5: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = b, AA' = c. Gọi M là trung điểm của B'C'. Mặt phẳng (MAC) chia khối lập phương thành hai phần. Tính thể tích mỗi phần theo a, b, c.
Câu 6: Cho 3 số không âm a, b, c thỏa mãn a2009 + b2009 + c2009 = 3. Tìm giá trị lớn nhất của biểu thức : P = a4 + b4 + c4
Câu 7: Cho mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): (x – 1)2 + (y + 2)2 = 9 và đường thẳng d: x + y + m = 0. Tìm m để trên đường thẳng d có điểm A mà từ đó kẻ được hai tiếp tuyến AB, AC tới đường tròn (C) (B, C là hai tiếp điểm) sao cho tam giác ABC vuông.
Câu 8: Trong không gian với trục tọa độ Oxyz, cho hai mặt phẳng 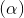 : x + y - 3z - 2 = 0 và (P): x + 2y - z - 4 = 0. Viết phương trình đường thẳng ∆ đi qua điểm M(1; 0; -2) song song với mặt phẳng
: x + y - 3z - 2 = 0 và (P): x + 2y - z - 4 = 0. Viết phương trình đường thẳng ∆ đi qua điểm M(1; 0; -2) song song với mặt phẳng 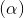 đồng thời tạo với mặt phẳng (P) một góc
đồng thời tạo với mặt phẳng (P) một góc 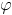 = 30°.
= 30°.
Câu 9: Có bao nhiêu số tự nhiên có 6 chữ số khác nhau mà trong mỗi số luôn luôn có mặt ba chữ số chẵn và ba chữ số lẻ, các chữ số chẵn không đứng cạnh nhau.
Câu 10: Cho hai đường thẳng: d1: 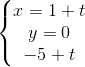 và d2:
và d2: 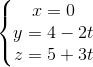 . Chứng minh d1 và d2 chéo nhau.
. Chứng minh d1 và d2 chéo nhau.
Câu 11: Cho hai đường thẳng: d1: 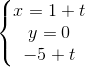 và d2:
và d2: 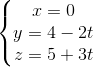 . Viết phương trình chính tắc của đường vuông góc chung của d1 và d2.
. Viết phương trình chính tắc của đường vuông góc chung của d1 và d2.
Câu 12: Tìm giới hạn 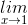
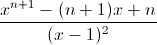 với n ∈ N*.
với n ∈ N*.
Câu 13: Giả bất phương trình:
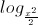 8 +
8 + 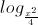 16 <
16 < 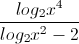 .
.