Đề thi thử Đại học môn Toán đề số 45

Câu 1: Cho hàm số: y = x³ + (m + 1)x² + (m² + 4m + 3)x +  (1). Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = - 3 (2). Với giá trị nào của m, hàm số có cực đại, cực tiểu? Gọi x₁ , x₂ là hai điểm cực đại, cực tiểu của hàm số, hãy tìm giá trị lớn nhất của biểu thức: A = |x₁.x₂ – 2(x₁ + x₂)|.

Câu 2: Giải phương trình: 3tan3x + cot2x = 2tanx +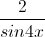 

Câu 3: Giải bất phương trình: 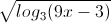 ≤ log₃ (x - )

Câu 4: Cho tứ diện OABC có cạnh OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC = a. Gọi K, M, N lần lượt là trung điểm của AB, BC, CA và E là điểm đối xứng của O qua K. Gọi I là giao điểm của CE với mặt phẳng (OMN) (1). Chứng minh CE vuông góc với mặt phẳng (OMN) (2). Tính diện tích tứ giác OMIN theo a.

Câu 5: Giải hệ phương trình:

Câu 6: Cho hai đường thẳng: ∆₁: x + y – 2 = 0 ∆₂: 2x – y – 1 = 0 Và điểm M(-6 ; 0) Viết phương trình đường thẳng qua M và cắt ∆₁, ∆₂ tại 2 điểm A và B sao cho M là trung điểm của AB

Câu 7: Tìm tập hợp các điểm biểu diễn của số phức z = m + 2i khi m thay đổi trong R

Câu 8: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A(2 ; -1) ; B(1 ; -2) và trọng tâm G của tam giác nằm trên đường thẳng d: x + y - 2 = 0. Hãy tìm tọa độ điểm C, biết diện tích tam giác bằng