Đề thi thử Đại học môn Toán đề số 47

Đề thi thử Đại học môn Toán đề số 47

Thời gian thi : 180 phút - Số câu hỏi : 10 câu - Số lượt thi : 290

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số: y = x³ – 3mx² + 4m (C_m) (1). Khảo sát và vẽ đồ thị hàm số khi m = 1 (2). Tìm tất cả các giá trị của m để (C_m) có các điểm cực trị đối xứng nhau qua đường thẳng: y = x

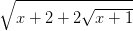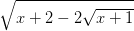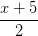
Câu 2: Giải phương trình: $\dpi{100} \sqrt{x+2+2\sqrt{x+1}}$ + $\dpi{100} \sqrt{x+2-2\sqrt{x+1}}$ = $\dpi{100} \frac{x+5}{2}$

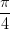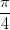Câu 3: Giải phương trình: sin⁴ (3x + $\dpi{100} \frac{\pi }{4}$ ) + sin⁴ (3x - $\dpi{100} \frac{\pi }{4}$ ) = $\dpi{100} \frac{1}{2}$

Câu 4: Trong mặt phẳng (P) cho đường tròn (C) tâm O, đường kính AB = 2R. Cho O₁ là điểm đối xứng của O qua A. Lấy điểm S sao cho SO₁ ⊥ (P) và SO₁ = 2R. Tính thể tích của khối cầu đi qua đường tròn O và điểm S.

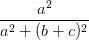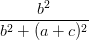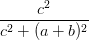Câu 5: Cho a, b, c là các số thực ≠ 0. Chứng minh bất đẳng thức sau: $\dpi{100} \frac{a^{2}}{a^{2}+(b+c)^{2}}$ + $\dpi{100} \frac{b^{2}}{b^{2}+(a+c)^{2}}$ + $\dpi{100} \frac{c^{2}}{c^{2}+(a+b)^{2}}$ ≥ $\dpi{100} \frac{3}{5}$

Câu 6: Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1 ; -1 ; 2) và B(3 ; 1 ; 0) và mặt phẳng (P) có phương trình: x - 2y - 4z + 8 = 0. Lập phương trình đường thẳng d thỏa mãn đồng thời các điều kiện sau: d nằm trong mặt phẳng (P), d ⊥ AB và d đi qua giao điểm của AB và mặt phẳng (P).

Câu 7: Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1 ; -1 ; 2) và B(3 ; 1 ; 0) và mặt phẳng (P) có phương trình: x - 2y - 4z + 8 = 0. Tìm tọa độ điểm C nằm trong mặt phẳng (P) sao cho CA = CB và mặt phẳng (ABC) vuông góc với mặt phẳng (P).

Câu 8: Giải hệ phương trình: 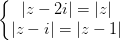$\dpi{100} \left\{\begin{matrix} |z-2i|=|z|\\ |z-i|=|z-1| \end{matrix}\right.$

Câu 9: Trong không gian Oxyz cho họ đường thẳng d_K là giao tuyến cảu các mặt phẳng (P_K): x – ky + z – k = 0 (Q_K): kx + y – kz – 1 = 0. Chứng minh rằng trong mặt phẳng (Oxy) đường thẳng ∆_K luôn luôn tiếp xúc với một đường tròn cố định.

Câu 10: Tìm hệ số của x¹⁸ trong khai triển nhị thức Niu-tơn (2 – x²)³ⁿ biết n thỏa mãn 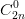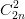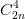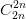$\dpi{100} C_{2n}^{0}$ + $\dpi{100} C_{2n}^{2}$ + $\dpi{100} C_{2n}^{4}$ + ... + $\dpi{100} C_{2n}^{2n}$ = 512