Đề thi thử đại học môn Toán đề số 52
Thời gian thi : 180 phút - Số câu hỏi : 11 câu - Số lượt thi : 257
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Cho hàm số: y=-x3-3x2+4. (a) khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho (HS tự làm). (b) Tìm a để đường thẳng nối điểm cực đại, cực tiểu của (C) tiếp xúc với đường tròn (Ca) có phương trình: (x-a)2+(y-a-1)2=5
Câu 2: Giải phương trình: (x2-5x+2)2-5(x2-5x+2)+2-x=0
Câu 3: Tính các góc của tam giác ABC thỏa mãn bất đẳng thức: sin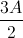 +sin
+sin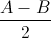 +sin
+sin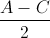 =
= (A,B,C là ba góc của tam giác)
(A,B,C là ba góc của tam giác)
Câu 4: Tính tích phân I=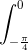
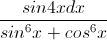
Câu 5: Cho x≥0; y≥0 và 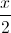 +y=1. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
+y=1. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức: 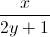 +
+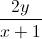
Câu 6: Xác định tâm và bán kính đường tròn đi qua ba điểm: A(2;-1); B(-1;-2); C(3;0)
Câu 7: Viết phương trình đường thẳng đi qua A(-1;1;2) song song với mặt phẳng (P):x-y-z+5=0 đồng thời vuông góc với đường thẳng: 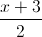 =
=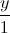 =
=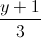
Câu 8: Viết phương trình đường thẳng qua điểm (1;0) và tạo với đường thẳng có phương trình: x+3y-5=0 một góc 45o
Câu 9: Cho đường thẳng d: 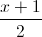 =
=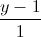 =
=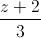 và mặt phẳng (P): x+y+z+8=0. Gọi A là giao điểm của d với mặt phẳng (P). Viết phương trình đường thẳng ∆ qua A vuông góc với d và năm trong mặt phẳng (P).
và mặt phẳng (P): x+y+z+8=0. Gọi A là giao điểm của d với mặt phẳng (P). Viết phương trình đường thẳng ∆ qua A vuông góc với d và năm trong mặt phẳng (P).
Câu 10: Tìm số phức z thỏa mãn đẳng thức: (z+i)(1+2i)+(1+zi)(3-4i)=1+7i
Câu 11: Giải phương trình:
 +7
+7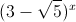 =2x+3.
=2x+3.