Đề thi thử đại học môn Toán lần I năm 2012 - trường THPT chuyên ĐHSP Hà Nội

Đề thi thử đại học môn Toán lần I năm 2012 - trường THPT chuyên ĐHSP Hà Nội

Thời gian thi : 180 phút - Số câu hỏi : 8 câu - Số lượt thi : 287

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số y=x³+2(m-1)x²+(m²-4m+1)x-2(m²+1) (1) 1.khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m=0 (học sinh tự giải) 2.Tìm các giá trị của m để hàm số có cực đại, cực tiểu và đường thẳng đi qua các điểm cực đại, cực tiểu của đồ thị hàm số (1) vuông góc với đường thẳng y= $\frac{9}{2}$ x+5

Câu 2: Giải phương trình: sin7x+sin9x=2[cos²( 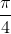$\frac{\pi }{4}$ -x)-cos²( 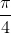$\frac{\pi }{4}$ +2x)]

Câu 3: Giải bất phương trình: 9x²+2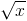 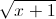$\sqrt{x}$ > $\sqrt{x+1}$ +1

Câu 4: Giải phương trình: 2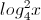 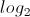$log_{4}^{2}x$ = $log_{2}$ x. $log_{2}$ ( $\sqrt{2x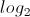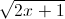+1}$ -1)

Câu 5: Cho hình chóp S.ABC có hình chiếu của đỉnh S lên mặt phẳng đáy nằm trong tam giác ABC, các mặt bên tạo với đáy góc 60^o ,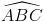 $\widehat{ABC}$ =60^o ,AB=4a, AC=2 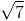$\sqrt{7}$ a. Tính thể tích hình chóp S.ABC

Câu 6: Cho các số thực a,b∈(0;1) Chứng minh rằng: 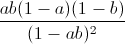$\frac{ab(1-a)(1-b)}{(1-ab)^{2}}$ < $\frac{1}{4}$

Câu 7: Trong mặt phẳng Oxy, cho tam giác ABC vuông tại A có các đỉnh A,B thuộc đường thẳng y=2; phương trình cạnh BC: 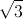$\sqrt{3}$ x-y+2=0. Tìm tọa độ tâm G của tam giác, biết bán kính đường tròn nội tiếp tam giác bằng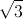 $\sqrt{3}$

Câu 8: Viết phương trình đường tròn đi qua hai điểm M(1;1) và N(2;4) và tiếp xúc với đường thẳng ∆: 2x-y-9=0

Bạn có đủ giỏi để vượt qua

nguyen van hien

Xếp hạng

Thành viên

Đúng

Làm

Đạt

Phút

nguyen van hien

8.47

Cùng tham gia trao đổi với bạn bè!

Lớp 12