Đề thi thử ĐH môn Toán lần V năm 2012 trường THPT chuyên ĐHSP HN

Thời gian thi : 120 phút - Số câu hỏi : 9 câu - Số lượt thi : 130

Click vào đề thi   Tải đề

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Cho hàm số: y = 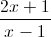\frac{2x+1}{x-1}. (1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. (HS tự làm) (2). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến tạo với đường tiệm cận của (C) một tam giác vuông cân.

Câu 2: Giải phương trình: 1+ sin x + cos x = 2 cos 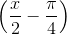\left ( \frac{x}{2}- \frac{\pi }{4} \right )

Câu 3: Giải phương trình: 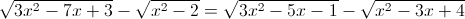   \sqrt{3x^{2}-7x+3}-\sqrt{x^{2}-2}=\sqrt{3x^{2}-5x-1}-\sqrt{x^{2}-3x+4}

Câu 4: Tính tích phân I = 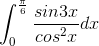\int_{0}^{\frac{\pi }{6}}\frac{sin3x}{cos^{2}x}dx

Câu 5: Cho lăng trụ ABC.A'B'C' có các cạnh bên là các hình vuông cạnh bằng a. Gọi D,E,F lần lượt là trung điểm các cạnh BC,A'C,B'C. Tính khoảng cách giữa hai đường thẳng DE và A'F theo a.

Câu 6:   Cho các số thực dương a,b,c thỏa mãn 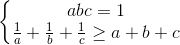 \left\{\begin{matrix} abc=1\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq a+b+c \end{matrix}\right. .  Chứng minh rằng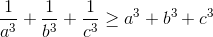 \frac{1}{a^{3}}+\frac{1}{b^{3}}+\frac{1}{c^{3}}\geq a^{3}+b^{3}+c^{3}

Câu 7: Trong mặt phẳng Oxy cho tam giác ABC với đường cao AH có phương trình 3x + 4y + 10 = 0 và đường phân giác trong BE có phương trình x - y + 1 = 0. Điểm M(0;2) thuộc đường thẳng AB và cách đỉnh C một khoẳng bằng √2.Tính diện tích tam giác ABC 

Câu 8: Trong không gian Oxyz cho mặt phẳng và đường thẳng lần lượt có phương trình (P): x + 2y - z + 5 = 0 và (d) : 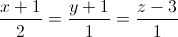\frac{x+1}{2}=\frac{y+1}{1}=\frac{z-3}{1}.  Viết phương trình mặt phẳng (Q) chứa đường thẳng d và tạo với mặt phẳng (P) một góc bằng 30° .

Câu 9: Giải phương trình sau trên tập số phức : z4 – 4z3  + 11z2 – 14z + 10 = 0

Bạn có đủ giỏi để vượt qua

laotan999 phamtan
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 phamtan 3 5 60% 56.3
2 Nhi Yến 1 1 100% 4.32
3 nguyen duc phong 0 1 0% 0.88
4 Nguyễn Văn Hòa 2 9 22% 4.8

Cùng tham gia trao đổi với bạn bè!

Lớp 12