Đề thi vào lớp 10 môn Toán chuyên Lê Quý Đôn tỉnh Bình Định năm 2013

Thời gian thi : 120 phút - Số câu hỏi : 11 câu - Số lượt thi : 740

Click vào đề thi  

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Cho biểu thức D=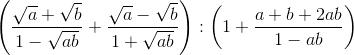\left ( \frac{\sqrt{a}+\sqrt{b}}{1-\sqrt{ab}}+ \frac{\sqrt{a}-\sqrt{b}}{1+\sqrt{ab}} \right ): \left ( 1+\frac{a+b+2ab}{1-ab} \right )

với a>0, b>0, ab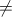\neq 1

Câu 1: Rút gọn D.

Câu 2: Tính giá trị của D với a= 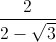\frac{2}{2-\sqrt{3}}

Giải phương trình và hệ phương trình sau:

Câu 3: Giair phương trình : 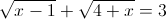\sqrt{x-1}+\sqrt{4+x}=3

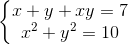
Câu 4: Giải hệ phương trình:  \left\{\begin{matrix} x+y+xy=7\\ x^{2}+y^{2} =10 \end{matrix}\right.

Trên mặt phẳng tọa độ Oxy cho Parabol (P) là đồ thị của hàm số y= 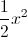\frac{1}{2}x^{2} và đường thẳng (d) có hệ số góc m và đi qua điểm I(0;2)

Câu 5: Viết phương trình đường thẳng d.

Câu 6: Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

Câu 7: Gọi 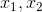x_{1}, x_{2} là hoành độ giao điểm của (d) và (P). Tìm giá trị của m để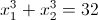 x_{1}^{3}+x_{2}^{3}=32

Từ điểm A ở ngoài đường tròn O kẻ hai tiếp tuyến AB,AC tới đường tròn (B,C là các tiếp điểm). Đường thẳng qua A cắt đường tròn (O) tại D và E ( D nằm giữa A và E, dây DE không đi qua tâm O).Gọi K\H là trung điểm của DE, AE cắt BC tại K.

Câu 8: Chứng minh rằng 5 điểm A,B,H,O,C cùng nằm trên một đường tròn.

Câu 9: Chứng minh 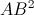AB^{2} = AD.AE

Câu 10: Chứng minh 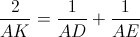\frac{2}{AK}=\frac{1}{AD}+\frac{1}{AE}

Câu 11: Cho 3 số: a, b, c khác 0 thỏa mãn : 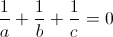\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0

Chứng minh rằng 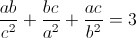\frac{ab}{c^{2}}+\frac{bc}{a^{2}}+\frac{ac}{b^{2}}=3

Bạn có đủ giỏi để vượt qua

ngocboong Lê Ngọc Anh
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 Lê Ngọc Anh 9 11 82% 32
2 Baokute Nhontho 5 11 45% 0.85
3 Diep Le 4 11 36% 1.37
4 Dinh Quoc Thai 3 11 27% 0.72
5 Candy Ngot Ngao 3 11 27% 0.87
6 Linh Linh'ss 2 11 18% 1.17
7 le thi kim oanh 3 11 27% 0.93
8 Vũ Lạc Hoan 2 11 18% 20.35
9 Trịnh Kiều Thanh 2 11 18% 3.93

Cùng tham gia trao đổi với bạn bè!

Lớp 9