Đề thi vào lớp 10 môn Toán chuyên TP.HCM năm 2013
Thời gian thi : 120 phút - Số câu hỏi : 7 câu - Số lượt thi : 685
Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"
Một số câu hỏi trong đề thi
Câu 1: Giải phương trình:
= 
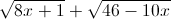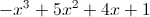
Câu 2: Cho đa thức bậc 3: f(x)= ax3 + bx2 +cx +d với a là một số nguyên dương và f(5)-f(4)=2012.Chứng minh rằng f(7) – f(2) là một hợp số.
Cho đường tròn (O) có tâm O và đường tròn (I) có tâm I, chúng cắt nhau tại hai điểm phân biệt A và B ( O và I nằm khác phía đối với đường thẳng AB). Đường thẳng IB cắt (O) tại điểm thứ 2 là F. Đường thẳng qua B song song với EFcắt (O) tại N.
Câu 3: Chứng minh: Tứ giác AOEF nội tiếp.
Câu 4: Chúng minh : MN=AE+EF
Câu 5: Cho a, b, c là các số thực dương thay đổi thỏa mãn điều kiện a+b+c=1.Tìm giá trị nhỏ nhất của biểu thức: F=14(a2 +b2 +c2) +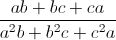 
.
Câu 6: Cho tứ giác nội tiếp ABCD có AC vuông góc với BD tại H. Gọi M là điểm trên cạnh AB sao cho AM = 
AB và N là trung điểm của HC. Chứng minh rằng đường thẳng DN vuông góc với đường thẳng MH.
Câu 7: Trong mặt phẳng cho 2013 điểm phân biệt sao cho với 3 điểm bất kỳ trong 2013 điểm đã cho luôn tồn tại 2 điểm có khoảng cách giữa chúng nhỏ hơn 1. Chứng minh rằng tồn tại một hình tròn bán kính bằng 1 chưa ít nất 1007 điểm trong 2013 điểm đã cho( hình tròn ở đây kể cả biên).
Bạn có đủ giỏi để vượt qua
| Xếp hạng | Thành viên | Đúng | Làm | Đạt | Phút |
| 1 |
Nguyễn Hữu Toàn |
5 | 7 | 71% | 22.62 |
| 2 |
kanna |
4 | 7 | 57% | 1.27 |
| 3 |
|
3 | 7 | 43% | 11.43 |
| 4 |
Danh Tuấn |
3 | 7 | 43% | 0.87 |
| 5 |
|
2 | 7 | 29% | 0.37 |