Đề thi vào lớp 10 môn Tóan tỉnh Khánh Hòa năm 2012

Thời gian thi : 120 phút - Số câu hỏi : 9 câu - Số lượt thi : 767

Click vào đề thi   Tải đề

Chú ý: Để xem lời giải chi tiết vui lòng chọn "Click vào đề thi"

Một số câu hỏi trong đề thi

Câu 1: Đơn giản biểu thức : A = 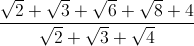\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}

Câu 2: Cho biểu thức : P = a – (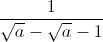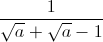\frac{1}{\sqrt{a}-\sqrt{a}-1} - \frac{1}{\sqrt{a}+\sqrt{a}-1}) ; (a  ≥ 1) . Rút gọn P và chứng tỏ P  ≥ 0

Câu 3: Cho phương trình bậc hai x2 + 5x + 3 = 0 có hai nghiệm x1; x2. Hãy lập một phương trình bậc hai có hai nghiệm (x12 + 1) và (x22 + 1).

Câu 4: Giải hệ phương trình 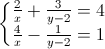\left\{\begin{matrix}\frac{2}{x}+\frac{3}{y-2}=4\\\frac{4}{x}-\frac{1}{y-2}=1\end{matrix}\right.

Câu 5: Quãng đường từ A đến B dài 50km. Một người dự định đi xe đạp từ A đến B với vận tốc không đổi. Khi đi được hai giờ, người ấy dừng lại 30 phút để nghỉ. Muốn đến B đứng thời gian dự định , người đó phải tăng vận tốc thêm 2km/h trên quãng đường còn lại. Tính vận tốc ban đầu của người đi xe đạp.

Cho tam giác ABC có ba góc nhọn và H là trực tâm. Vẽ hình bình hành BHCD. Đường thẳng đi qua D và song song BC cắt đường thẳng AH tại E.

Câu 6: Chứng minh A, B, C, D , E cùng thuộc một đường tròn.

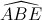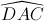
Câu 7: Chứng minh \widehat{ABE} = \widehat{DAC}

Câu 8: Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và M là trung điểm BC, đường thẳng AM cắt OH tại G. Chứng minh G là trọng tâm của tam giác ABC.

Câu 9: Giả sử OD = a. Hãy tính độ dài đường tròn ngoại tiếp tam giác BHC theo a.

Bạn có đủ giỏi để vượt qua

daigiahuong99 abcdefghik
Xếp hạng Thành viên Đúng Làm Đạt Phút
1 abcdefghik 8 9 89% 5.63
2 Lê Ngọc Anh 6 9 67% 28.2
3 Diep Le 4 9 44% 2.98
4 TK Đoàn 9 9 100% 21.28
5 Chan Aily 4 9 44% 3.85
6 Linh Linh'ss 2 9 22% 1.85
7 Đinh Thu Huyên 3 9 33% 7.23
8 Baokute Nhontho 0 0 0% 0.05
9 Trần Văn Tâm 0 0 0% 0.63
10 Vũ Lạc Hoan 1 9 11% 11.2
11 Nguyệt Hà 1 9 11% 5.92
12 Nhok Con 0 9 0% 3.62

Cùng tham gia trao đổi với bạn bè!

Lớp 9