Phần 1: Toán học và xử lý số liệu
Một vật được ném xiên với vận tốc ban đầu \(v_0=50 \mathrm{~m} / \mathrm{s}\) hợp với phương ngang một góc \(\theta=45^{\circ}\). Tầm xa của vật được tính bởi: \(R=\dfrac{v_0^2 \sin 2 \theta}{g}\) với \(g=9.8 \mathrm{~m} / \mathrm{s}^2\). Tính tầm xa \(R\) (làm tròn đến chữ số thập phân hàng đơn vị).
Đáp án đúng là: 255
Thay các giá trị \(v_0\), (\theta\) và \(g\) vào hàm số \(R=\dfrac{v_0^2 \sin 2 \theta}{g}\) để tính giá trị \(R\)
Đáp án cần điền là: 255
Tìm tất cả tham số \(m\) để: \(f(x)=(m-1) x^2+2(m-1) x+m-3\) không dương với mọi \(x \in \mathbb{R}\).
Đáp án đúng là: A
\(f(x) \leq 0 \forall x \in \mathbb{R} \Leftrightarrow\left\{\begin{array} { l } { a < 0 } \\{ \Delta ^ { \prime } \leq 0 }\end{array}\right.\)
Đáp án cần chọn là: A
Một công ty tuyển dụng nhân viên mới với mức lương là 125 triệu đồng cho năm đầu tiên. Mỗi năm tiếp theo, tiền lương nhân viên này được tăng thêm 25 triệu đồng cho đến khi đạt mức tối đa là 400 triệu đồng/năm. Tính tổng số tiền lương mà người nhân viên nhận được trong 15 năm đầu (đơn vị tính là triệu đồng).
Đáp án đúng là: 4350
Tính tổng số tiền lương mà người nhân viên nhận được cho đến khi đạt mức tối đa là 400 triệu đồng/năm theo công thức tính tổng của cấp số cộng: \(S=\dfrac{n\left(u_1+u_n\right)}{2}\).
Tổng số tiền lương người đó nhận được trong 15 năm bằng tổng số tiền người đó nhận được cho đến khi đạt mức tối đa là 400 triệu đồng và số tiền của những tháng đạt 400 triệu đồng.
Đáp án cần điền là: 4350
Tính tổng các giá trị của tham số \(m\) để phương trình \(x^3-7 x^2+2\left(m^2+6 m\right) x-8=0\) có ba nghiệm phân biệt lập thành một cấp số nhân.
Đáp án đúng là: -6
Sử dụng tính chất của cấp số nhân: \(x_1 x_3=x_2^2\).
Đáp án cần điền là: -6
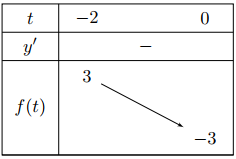
Một bể bơi chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng đồ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút. Gọi \(f(t)\) là hàm số biểu thị nồng độ muối trong bể sau \(t\) phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) xác định trên nửa khoảng \([0 ;+\infty]\). Khi nồng độ muối trong bể đạt trạng thái cân bằng thì nồng độ khi đó bằng bao nhiêu?
Đáp án đúng là: B
Xác định khối lượng muối trong bể và thể tích nước, từ đó xác định hàm \(f(t)\).
Tính giới hạn hàm số \(f(t)\) tại vô cùng.
Đáp án cần chọn là: B
Đạo hàm của hàm số \(y=\ln (\sin x)\) là
Đáp án đúng là: C
Áp dụng công thức: \((\ln u)'=\dfrac{u'}{u}\)
Đáp án cần chọn là: C
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để tập nghiệm của bất phương trình \(\left(3^{x+1}-\sqrt{3}\right)\left(3^x-2 m\right)<0\) khác rỗng và chứa không quá 5 số nguyên.
Đáp án đúng là: 121
Đáp án cần điền là: 121
Cho hàm số \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\) với \(f'(x)=x(x-2)^2(x-3)^3\). Hàm số đồng biến trên khoảng nào?
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho hàm số \(y=x^3-3 x^2+2 x\)., tiếp tuyến của đồ thị tại điểm \(x=1\) cắt trục hoành và trục tung tại các điểm \(A\) và \(B\). Tính diện tích tam giác \(O A B\).
Đáp án đúng là: 1/2
Đáp án cần điền là: 1/2
Cho hàm bậc bốn \(f(x)\). Đồ thị hàm số \(y=f^{\prime}(x)\) như hình vẽ. Hàm số \(g(x)=f(x)+4 x\) đồng biến trên khoảng nào?
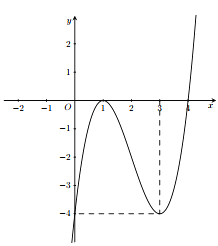
Đáp án đúng là: A
Đáp án cần chọn là: A
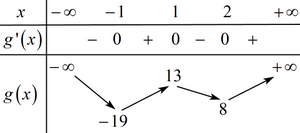
Cho hàm số \(f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và bảng xét dấu đạo hàm như sau

Khẳng định nào sau đây về số cực trị của hàm số \(g(x)=f\left(x^2+1\right)+x^2-x^3+x^4\) là đúng?
Đáp án đúng là: C
Đáp án cần chọn là: C
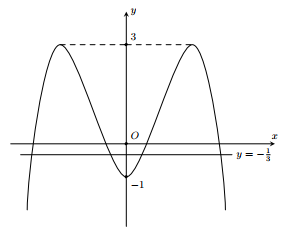
ho hàm số \(y=f(x)\) có bảng biến thiên như sau
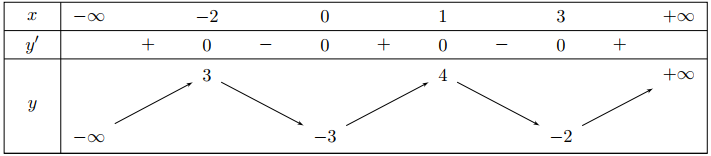
Giá trị lớn nhất của hàm số \(g(x)=f(\cos x-1)\) bằng
Đáp án đúng là: C
Đáp án cần chọn là: C
Gọi \(S\) là tập hợp tất cả các giá trị nguyên \(m\) để đồ thị hàm số \(y = \left| {3{x^4} - 8{x^3} - 6{x^2} + 24x - m} \right|\) có 7 điểm cực trị. Tính tổng các phần tử của \(S\).
Đáp án đúng là: D
Số điểm cực trị của hàm số \(y = \left| {f\left( x \right)} \right|\) với \(f\left( x \right)\) là hàm đa thức = số điểm cực trị của hàm số \(y = f\left( x \right)\) + số giao điểm (không tính điểm tiếp xúc) của đồ thị hàm số \(f\left( x \right)\) và trục hoành.
Đáp án cần chọn là: D
Tiệm cận xiên của đồ thị hàm số \(y=\dfrac{x^2-2 x+3}{x+1}\) là
Đáp án đúng là: C
Đáp án cần chọn là: C
Hàm số \(F\left( x \right) = \dfrac{1}{2}\sin 2x\) là một nguyên hàm của hàm số nào dưới đây?
Đáp án đúng là: C
Cho hàm số \(f(x)\) xác định trên \(K\).
Hàm số \(F(x)\) được gọi là nguyên hàm của hàm số \(f(x)\) trên \(K\) nếu \({F^\prime }(x) = f(x)\) với mọi \(x \in K\).
Đáp án cần chọn là: C
Cho hàm số \(y=f(x)\) có đồ thị như hình. Tìm số nghiệm của phương trình \(\dfrac{1-f(x)}{1+f(x)}=2\).
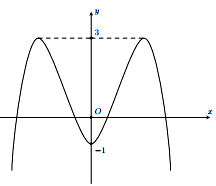
Đáp án đúng là: D
Đáp án cần chọn là: D
Một vật bắt đầu chuyến động \(v(t)=2 t^3-15 t^2+24 t+20(\mathrm{~m} / \mathrm{s})\). Hỏi trong 5 giây đầu tiên, quãng đường vật đi được cho đến khi đạt vận tốc lớn nhất là bao nhiêu?
Đáp án đúng là: D
Tìm thời điểm mà tại đó vận tốc đạt giá trị lớn nhất.
Ứng dụng tích phân tính quãng đường vật đi được.
Đáp án cần chọn là: D
Cho hàm số bậc bốn có đồ thị \(y=f^{\prime}(x)\) như hình vẽ. Tìm số điểm cực trị của hàm số \(y=f(x)\).
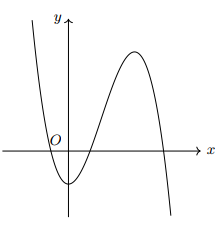
Đáp án đúng là: 3
Đáp án cần điền là: 3
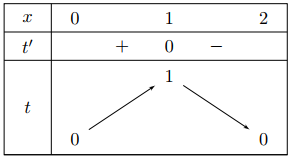
Cho hàm số \(f(x)\) có bảng biến thiên như hình:
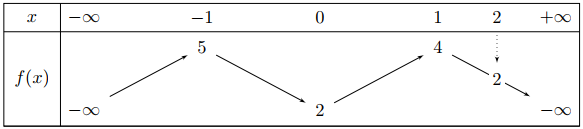
Phương trình \(f\left(\sqrt{2 x-x^2}\right)=3\) có bao nhiêu nghiệm?
Đáp án đúng là: B
Đáp án cần chọn là: B
Cho hàm số \(g(x)=x^3 \ln x\). Giá trị của \(\int_1^3\left(g^{\prime}(x)+\dfrac{x^2-6}{x}\right) d x\) là bao nhiêu? (kết quả làm tròn đến hàng đơn vị)
Đáp án đúng là: 27
Đáp án cần điền là: 27
Trong không gian \(O x y z\), cho mặt cầu \((S): x^2+(y-1)^2+z^2=2\). Trong các điểm dưới đây, điểm nào nằm ngoài mặt cầu \((S)\) ?
Đáp án đúng là: B
Đáp án cần chọn là: B
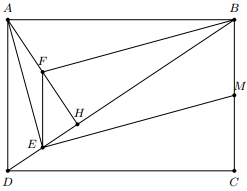
Từ vị trí \(A\) người ta quan sát một cây cao.
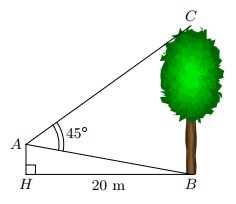
Biết \(A H=4(\mathrm{~m}), H B=20(\mathrm{~m}), \widehat{B A C}=45^{\circ}\). Khi đó chiều cao của cây là (tính chính xác đến hàng phần chục)
Đáp án đúng là: A
Áp dụng định lý sin cho tam giác.
Đáp án cần chọn là: A
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục $Ox$ tại $x = 1; x = 3$. Khi cắt một vật thể bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(1 \leq x \leq 3)$, mặt cắt là tam giác vuông có một góc $45^\circ$ và độ dài một cạnh góc vuông là $\sqrt{4 - \dfrac{1}{2}x^2}$. Tính thể tích vật thể trên, kết quả làm tròn đến hàng phần trăm.
Đáp án đúng là: 11/6
Tính diện tích hình tam giác vuông.
Sử dụng ứng dụng của tích phân để tính thể tích vật thể.
Đáp án cần điền là: 11/6
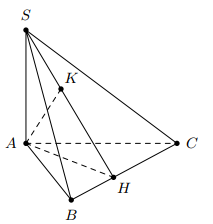
Cho hình chóp \(S \cdot A B C\) có đáy là tam giác vuông tại \(A\) có \(A B=a\), \(B C=a \sqrt{5}\). Biết \(S A=3 a\) và \(S A \perp(A B C)\). Tính khoảng cách từ \(A\) đến mặt phẳng \((S B C)\).
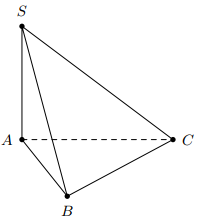
Đáp án đúng là: A
Đáp án cần chọn là: A
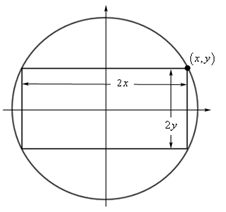
Một kiến trúc sư muốn thiết kế một khung cửa sổ hình chữ nhật lắp vào một ô tròn trên tường có bán kính 4 mét. Kiến trúc sư muốn cửa sổ có kích thước lớn nhất để đón ánh sáng vào căn phòng. Hỏi diện tích lớn nhất của cửa sổ có thể đạt được là bao nhiêu?
Đáp án đúng là: 32
- Bài toán yêu cầu tìm diện tích lớn nhất của hình chữ nhật nội tiếp hình tròn có bán kính bằng 4.
- Đặt trục tọa độ với tâm đường tròn trùng với gốc tọa độ. Lập phương trình đường tròn và biểu
diễn hàm diện tích của hình chữ nhật.
- Tính đạo hàm của hàm diện tích và tìm giá trị lớn nhất của hàm số.
Đáp án cần điền là: 32
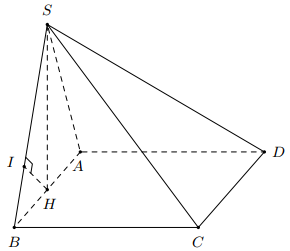
Cho hình chóp \(S \cdot A B C D\) có đáy \(A B C D\) là hình vuông cạnh \(2 a\), cạnh bên \(S A=a \sqrt{5}\), mặt bên \(S A B\) là tam giác cân đỉnh \(S\) và thuộc mặt phẳng vuông góc với mặt phẳng đáy (tham khảo hình bên). Tính khoảng cách giữa hai đường thẳng \(A D\) và \(S C\).
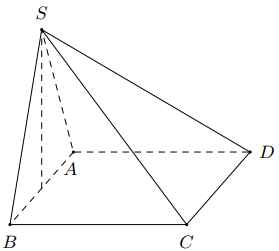
Đáp án đúng là: C
Đáp án cần chọn là: C
Cho \(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}(2 \tan x+\cot x)^2 \mathrm{~d} x=a+b \sqrt{3}+c \pi(*)\). Biết rằng, tồn tại duy nhất bộ ba số hữu tỉ \(a, b, c\) thỏa mãn (*). Tổng \(a+3b+12c\) có giá trị bằng bao nhiêu (nhập đáp án vào ô trống)?
Đáp án đúng là: 1
Đáp án cần điền là: 1
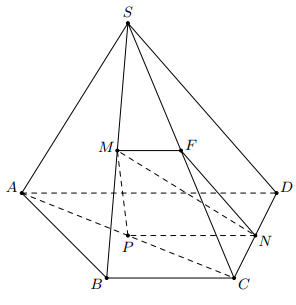
Cho hình chóp \(S \cdot A B C D\) có đáy \(A B C D\) là hình thang \((A D / / B C, 2 A D=5 B C)\). Gọi \(M, N, P\) lần lượt là trung điểm của \(S B, C D\) và \(A C\). Mặt phẳng \((M N P)\) cắt \(S C\) tại \(F\). Khi đó \(P N=k M F\). Giá trị của \(k\) bằng bao nhiêu?
Đáp án đúng là: B
Dùng quan hệ song song xác định điểm F từ đó tính tỉ lệ.
Đáp án cần chọn là: B
Đường tròn \((C)\) có tâm \(I\) thuộc đường thẳng \(d: x+3 y+8=0\), đi qua điểm \(A(-2 ; 1)\) và tiếp xúc với đường thẳng \(\Delta: 3 x-4 y+10=0\). Tính bán kính đường tròn \((C)\).
Đáp án đúng là: 5
Đáp án cần điền là: 5
Tính diện tích tam giác \(A B C\) với \(A(7 ; 3 ; 4), B(1 ; 0 ; 6)\) và \(C(4 ; 5 ;-2)\).
Đáp án đúng là: 49/2
Công thức tính diện tích tam giác: \(S_{\triangle A B C}=\dfrac{1}{2} \cdot|[\overrightarrow{A B}, \overrightarrow{A C}]|\)
Đáp án cần điền là: 49/2
Trong không gian tọa độ \(O x y z\) cho tam giác \(A B C\) có \(A(0 ; 2 ;-1) ; B(1 ; 0 ; 3) ; C(2 ; 4 ; 1)\) và \((P): 2 x+\) \(3 y-z+5=0\). Gọi \(M(a, b, c)\) là điểm thuộc mặt phẳng \((\mathrm{P})\) sao cho \(M A^2+M B^2+M C^2\) nhỏ nhất. Giá trị biểu thức \(7(a^2+b^2+c^2)\) là:
Đáp án đúng là: B
Đáp án cần chọn là: B
Trong không gian \(O x y z\), cho đường thẳng \((d): \dfrac{x-2}{1}=\dfrac{y+1}{-2}=\dfrac{z}{2}\) và điểm \(A(3,2,-1)\). Mặt phẳng \(P\) qua \(A\) và vuông góc với đường thẳng \((d)\) có phương trình là
Đáp án đúng là: B
Mặt phẳng vuông góc với đường thẳng nên vectơ pháp tuyến của mặt phẳng \((P)\) là vectơ chỉ phương của đường thẳng \((d)\).
Đáp án cần chọn là: B
Một hình cầu có bán kính 6 dm, người ta cắt bỏ hai phần bằng hai mặt phẳng song song và cùng vuông góc với đường kính để làm mặt xung quanh của một chiếc lu chứa nước (như hình vẽ). Tính thể tích \(V\)(lít) mà chiếc lu chứa được biết mặt phẳng cách tâm mặt cầu 4 dm (làm tròn đến hàng đơn vị).
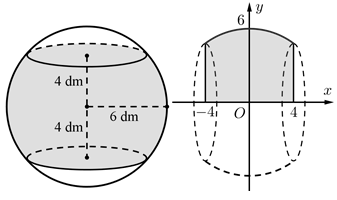
Đáp án đúng là: 771
Ứng dụng hình học của tích phân tích thể tích khối tròn xoay.
Đáp án cần điền là: 771
Trong không gian \(Oxyz\), cho các đường thẳng \(\left(d_1\right): \dfrac{x-1}{1}=\dfrac{y+2}{-2}=\dfrac{z+1}{2}\),\(\left(d_2\right): \dfrac{x+1}{2}=\dfrac{y-5}{3}=\dfrac{z}{-1}\) và điểm \(A(1,2,-1)\). Xét \(B(0, a, b)\) là một điểm trong không gian. Biết đường thẳng \(A B\) vuông góc với \(\left(d_1\right)\) và cắt đường thẳng \(\left(d_2\right)\). Đường thẳng \(A B\) song song với đường thẳng nào sau đây:
Đáp án đúng là: B
Đáp án cần chọn là: B
Trong không gian Oxyz , cho điểm \(A(1,1,3)\). Gọi \(H\) là hình chiếu của \(A\) lên đường thẳng \((l): \begin{cases}x & =1+t \\ y & =1+t \\ z & =t\end{cases}\). Gọi \(M\) là trung điểm của \(A H\) và \((P): x+b y+c y+d=0\) là mặt phẳng chứa \(M\) sao cho khoảng cách từ \(A\) tới \((P)\) bằng độ dài đoạn \(A M\). Tổng \(c+d\) bằng
Đáp án đúng là: A
Viết phương trình mặt phẳng đi qua M và nhận \(\overrightarrow{A H}\) làm vectơ pháp tuyến.
Đáp án cần chọn là: A
Trong không gian cho mặt cầu có phương trình \((x-5)^2+(y-3)^2+(z-1)^2=10\) và mặt phẳng \((P): 2 x-y-z=0\). Biết mặt cầu \((S)\) cắt mặt phẳng \((P)\) theo một đường tròn \((C)\). Chu vi đường tròn \((C)\) là:
Đáp án đúng là: B
Tính khoảng cách từ tâm mặt cầu đến mặt phẳng, áp dụng Py-ta-go để tính bán kính đường tròn.
Đáp án cần chọn là: B
Trong mặt phẳng tọa độ với hệ tọa độ \(O x y\), cho hình chữ nhật \(A B C D\) có điểm \(H(1 ; 2)\) là hình chiếu vuông góc của \(A\) lên \(B D\). Điểm \(M\left(\dfrac{9}{2} ; 3\right)\) là trung điểm cạnh \(B C\). Phương trình đường trung tuyến kẻ từ đỉnh \(A\) của tam giác \(A D H\) là \(4 x+y-4=0\). Biết điểm \(D\) có tọa độ là \(\left(x_D ; y_D\right)\) tính giá trị biểu thức \(S=14 x_D^2+y_D^2\).
Đáp án đúng là: 4
Đáp án cần điền là: 4
Khi ôn thi học sinh giỏi môn Toán, bạn Lan đã tự thống kê lại thời gian giải một bài tập nâng cao ở bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm là \(2,ab\). Tính \(a-b\)
Đáp án đúng là: 0
Tính số trung bình và phương sai của mẫu số liệu:
\(s^2=\dfrac{m_1\left(x_1-\bar{x}\right)^2+\ldots+m_k\left(x_k-\bar{x}\right)^2}{n}\)
Tính độ lệch chuẩn bằng cách tính căn bậc hai của phương sai.
Đáp án cần điền là: 0
Cho mẫu số liệu sau
\(27 ; \quad 15 ; \quad 18 ; \quad 30 ; \quad 19 ; \quad 40 ; \quad 100 ; \quad 9 ; \quad 46 ; \quad 10 ; \quad 200\)
Tứ phân vị thứ nhất bằng
Đáp án đúng là: B
Đáp án cần chọn là: B
Một đề thi trắc nghiệm gồm 50 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án đúng, mỗi câu trả lời đúng được 0,2 điểm. Một thí sinh làm hết bài thi bằng cách chọn ngẫu nhiên mỗi câu 1 phương án. Xác suất để thí sinh đó được đúng 8 điểm bằng
Đáp án đúng là: D
Gọi biến cố, sử dụng tổ hợp và tính xác suất theo nghĩa cổ điển
Đáp án cần chọn là: D
Trong một trường học, tỉ lệ học sinh chơi bóng đá là 0,3, tỉ lệ học sinh chơi bóng chuyền là 0,4 và tỉ lệ học sinh chơi cả hai môn thể thao là 0,1. Chọn ngẫu nhiên một học sinh trong trường học đó, xác suất để học sinh đó không chơi bất kỳ môn thể thao nào là
Đáp án đúng là: C
Sử dụng quy tắc công xác suất.
Đáp án cần chọn là: C
A và B chơi \(A\) và \(B\)ném bóng rổ độc lập với nhau. Biết rằng xác suất ném trúng của \(A\) là 0,6 , của \(B\) là 0,75 . Xác suất để chỉ một trong hai người ném trúng là
Đáp án đúng là: B
Đáp án cần chọn là: B
Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik \(3 \times 3\), bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
Đáp án đúng là: D
Đáp án cần chọn là: D
Trong cuộc khảo sát 300 gia đình ở một khu vực, người ta nhận thấy có \(90 \%\) gia đình có ti vi và \(60 \%\) gia đình có máy tính bàn. Mỗi gia đình đều có ít nhất một trong hai thiết bị này. Chọn ngẫu nhiên một gia đình. Tính xác suất gia đình đó có máy tính bàn trong nhóm các gia đình có ti vi.
Đáp án đúng là: C
Sử dụng công thức xác suất có điều kiện: \(\mathrm{P}(B \mid A)=\dfrac{n(A \cap B)}{n(A)}
Đáp án cần chọn là: C
Một căn bệnh có \(1 \%\) dân số mắc phải. Một phương pháp chuẩn đoán được phát triển có tỷ lệ chính xác là \(99 \%\). Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính \(99 \%\) số trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 99 trong 100 trường hợp. Nếu một người kiểm tra và kết quả là dương tính (bị bệnh) thì xác suất để người đó thực sự bị bệnh là bao nhiêu?
Đáp án đúng là: C
Áp dụng công thức Bayes: \(\mathrm{P}(A \mid B)=\dfrac{\mathrm{P}(A) \cdot \mathrm{P}(B \mid A)}{\mathrm{P}(A) \cdot \mathrm{P}(B \mid A)+\mathrm{P}(\bar{A}) \cdot \mathrm{P}(B \mid \bar{A})}\).
Đáp án cần chọn là: C
Bạn Uyên đập heo đất được 2 triệu đồng. Trong đợt quyên góp ủng hộ các bạn học sinh ở vùng bị bão lụt, Uyên đã ủng hộ \(x\) tờ tiền có mệnh giá 20000 đồng, \(y\) tờ tiền có mệnh giá 50000 đồng từ heo đất. Hỏi cặp số \((x ; y)\) nào thoả mãn tình huống này ?
Đáp án đúng là: B
Lập bất phương trình biểu diễn tổng số tiền Uyên quyên góp theo x và y.
Thay giá trị của từng cặp \((x,y)\) trong các ý để kiểm tra.
Đáp án cần chọn là: B
Lúc 3 giờ 00 sáng, kim phút và kim giờ của đồng hồ tạo thành góc vuông. Biết rằng sau ít nhất \(t\) phút thì kim phút và kim giờ lại tạo thành góc vuông. Hỏi \(t\) gần nhất với giá trị nào sau đây?
Đáp án đúng là: B
Đáp án cần chọn là: B
Dân số thành phố Hà Nội năm 2022 khoảng 8,4 triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Hà Nội không đổi và bằng \(r=1,04 \%\). Biết rằng, sau \(t\) năm dân số Hà Nội (tính từ mốc 2022) ước tính theo công thức \(S=A \cdot \mathrm{e}^{r t}\), trong đó \(A\) là dân số năm lấy mốc.
Trả lời cho các câu 48, 49, 50 dưới đây:
Vào năm 2030 dân số thành phố Hà Nội là bao nhiêu triệu người (kết quả làm tròn đến hàng phần trăm)?
Đáp án đúng là: C
Đáp án cần chọn là: C
Vào năm nào thì dân số của Hà Nội vượt quá 10 triệu người?
Đáp án đúng là: A
Đáp án cần chọn là: A
Hỏi sau bao nhiêu năm thì dân số Hà Nội gấp đôi thời điểm hiện tại?
Đáp án đúng là: A
Đáp án cần chọn là: A
Phần 2: Văn học - Ngôn Ngữ
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Căn cứ kiến thức về nghĩa của từ
Đáp án cần chọn là: B
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Căn cứ kiến thức về nghĩa của từ
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Căn cứ kiến thức về nghĩa của từ
Đáp án cần chọn là: A
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Căn cứ kiến thức về nghĩa của từ
Đáp án cần chọn là: B
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: B
Căn cứ kiến thức về nghĩa của từ
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Bản tính thích ứng nhanh sẽ giúp nhân dân ta ________ những cơ hội, ứng phó với ________ do tiến trình hội nhập mang lại.
Đáp án đúng là: C
Đọc, phân tích, suy luận
Đáp án cần chọn là: C
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Ở tác phẩm kí văn học, tác giả ________ thành một nhân vật trong tác phẩm, giữ vai trò tự thuật, trò chuyện với các nhân vật khác, trình bày các sự kiện bằng việc sử dụng ________ để quan sát, liên tưởng và tưởng tượng, bộc lộ những ấn tượng, ý kiến, tình cảm của mình.
Đáp án đúng là: B
Đọc, phân tích, suy luận
Đáp án cần chọn là: B
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Văn học dân gian là những tác phẩm nghệ thuật ngôn từ ________ , là sản phẩm của quá trình ________ tập thể để thể hiện nhận thức, tư tưởng, tình cảm của nhân dân lao động.
Đáp án đúng là: A
Đọc, phân tích, suy luận
Đáp án cần chọn là: A
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Rất nhiều câu chuyện buồn vẫn còn xảy ra ở quê tôi chỉ vì cái ________ ghen ăn tức ở, con gà tức nhau tiếng gáy vẫn còn ________ bén rễ trong tiềm thức của người dân.
Đáp án đúng là: A
Đọc, phân tích, suy luận
Đáp án cần chọn là: A
Chọn cặp từ/cụm từ thích hợp nhất điền vào chỗ trống:
Tộc phả là quyển cổ biên tên từ ông thủy tổ ________ lần lượt theo thứ tự các ngành trong họ cho đến ________ .
Đáp án đúng là: B
Đọc, phân tích, suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Khi đến thăm vùng đất chín rồng khí hậu quanh năm mát mẻ, với những vườn cây trái sum suê, những cây cảnh quý lại được chăm sóc khéo léo bởi các nghệ nhân tài hoa, đối với các du khách trong và ngoài nước sẽ có những trải nghiệm thú vị và bổ ích.
Đáp án đúng là: D
Đọc, phân tích, suy luận
Đáp án cần chọn là: D
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Việc một số công ty du lịch tổ chức các tour đón khách đến nghỉ ngơi, tắm biển được mở ra tại đây đã làm cho bãi biển khu vực này dần trở thành một khu du lịch nổi tiếng.
Đáp án đúng là: B
Đọc, phân tích, suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Kể từ đó, cả con hẻm 84 này lúc nào cũng chìm trong nỗi kinh hoàng của ma túy gây ra, không người nào dám bén mảng ra ngoài đường sau mười giờ đêm.
Đáp án đúng là: C
Đọc, phân tích, suy luận
Đáp án cần chọn là: C
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Trong xu hướng của giáo dục hiện đại, việc cho các em học sinh tham gia các chuyến thăm quan thực tế là một hoạt động vô cùng bổ ích, lí thú.
Đáp án đúng là: B
Đọc, phân tích, suy luận
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Mặc dù các lực lượng chức năng đã hết sức cố gắng nhưng đám cháy vẫn cứ loang rộng với một tốc độ khó kiểm soát.
Đáp án đúng là: C
Đọc, phân tích, suy luận
Đáp án cần chọn là: C
Đọc đoạn trích dưới đây và trả lời các câu hỏi 66 đến 70:
Sự ngưng tụ hơi nước là quá trình hơi nước trong không khí được chuyển sang thể nước lỏng. Ngưng tụ hơi nước rất quan trọng đối với chu trình tuần hoàn nước bởi nó hình thành nên những đám mây. Những đám mây này có thể tạo ra mưa, nó là cách chính để nước quay trở lại trái đất. Ngưng tụ hơi nước là quá trình ngược với bốc hơi nước. Sự ngưng tụ hơi nước cũng là nguyên nhân của hiện tượng sương, hoặc nước trên mắt kính của bạn khi bạn từ một phòng lạnh đi ra ngoài trong một ngày nóng, ẩm ướt, còn trong một ngày lạnh nước có thể nhỏ giọt bên ngoài cốc uống nước của bạn hay có nước ở phía bên trong cửa sổ ngôi nhà bạn.
Thậm chí trên những bầu trời trong xanh không một gợn mây, thì nước vẫn tồn tại dưới hình thức hơi nước và những giọt nước li ti không thể nhìn thấy được. Những phân tử nước kết hợp với những phân tử nhỏ bé của bụi, muối, khói trong khí quyển để hình thành nên các hạt nhân mây (giọt mây nhỏ, đám mây nhỏ), nó gia tăng khối lượng và phát triển thành những đám mây. Khi những giọt nước kết hợp với nhau, gia tăng về kích thước, những đám mây có thể phát triển và mưa có thể xảy ra. Các đám mây hình thành trong khí quyển do không khí chứa hơi nước bốc lên cao và lạnh đi. Phần quan trọng của quá trình này là không khí sát mặt đất ấm lên do bức xạ mặt trời. Nguyên nhân lớp khí quyển phía bên trên mặt đất lạnh đi là do áp lực không khí.
(Trích “Bách khoa từ điển về khí hậu và thời tiết”, theo Gleick)
Trả lời cho các câu 66, 67, 68, 69, 70 dưới đây:
Đoạn trích thuộc phong cách ngôn ngữ nào?
Đáp án đúng là: D
Căn cứ 6 phong cách ngôn ngữ đã học (sinh hoạt, nghệ thuật, chính luận, báo chí, khoa học, hành chính).
Đáp án cần chọn là: D
Theo đoạn trích, đám mây được hình thành KHÔNG do điều kiện nào dưới đây:
Đáp án đúng là: A
Đọc tìm ý
Đáp án cần chọn là: A
Dòng nào nêu chính xác nội dung của đoạn trích trên?
Đáp án đúng là: D
Đọc, tổng hợp
Đáp án cần chọn là: D
Sự ngưng tụ hơi nước KHÔNG là nguyên nhân của hiện tượng nào sau đây?
Đáp án đúng là: C
Phân tích, lý giải, tổng hợp
Đáp án cần chọn là: C
Theo tác giả, quá trình hơi nước trong không khí được chuyển sang thể nước lỏng được gọi là gì?
Đáp án đúng là: A
Đọc, phân tích, suy luận
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 71 đến 75:
“Có người nghĩ rằng cần có nhiều tiền mới có thể hưởng thụ thực sự. Nhưng không. Với tiền, bạn có thể sở hữu nhiều thứ. Nhưng chỉ sở hữu thôi thì không mang lại hạnh phúc. Và chỉ sở hữu, không có nghĩa là biết hưởng thụ. Một người biết tận hưởng chiếc máy ảnh xịn khác với một người sở hữu máy ảnh chỉ vì muốn người khác khen là nó rất xịn. Một người thực sự hiểu, và biết tận hưởng tốc độ, tiện nghi của chiếc xe hơi khác với một người mua nó chỉ vì tin rằng việc sở hữu nó sẽ chứng tỏ mình thành đạt. Một người thực sự am hiểu hội họa, và biết giá trị của bức tranh mình mua sẽ rất khác một người bỏ nhiều tiền mua tranh chỉ để nghe những lời trầm trồ của người khác trong phòng khách nhà mình.
Có người nghĩ rằng hưởng thụ cuộc sống đồng nghĩa với vật chất. Nhưng không. Hưởng thụ cuộc sống tức là tận hưởng mọi thứ tốt đẹp mà cuộc đời và vũ trụ mang đến cho bạn. Vật chất, tinh thần, thể xác. Cổ điển hay hiện đại. Nắng và gió, ngày và đêm. Mặt trời, mặt trăng, cây cối, núi sông và cỏ dại. Tình bạn, tình yêu. Mọi thứ, nếu bạn có thể nhận ra. Đáng buồn là nhiều lúc, chúng ta không nhận ra chúng, mà chỉ nhìn thấy những ảo ảnh khác. Chúng ta bị ảo giác. Chúng ta chỉ sở hữu mà cứ ngỡ mình đang được hưởng thụ. Đó là một ảo giác. Hoặc chúng ta đang trải qua điều này mà cứ tưởng rằng mình đang hưởng thụ một điều khác. Đó là một ảo giác khác. Ví như khi bạn tưởng mình đang tận hưởng một tình yêu say đắm, nhưng thật ra, chỉ là những thỏa mãn nhục dục. Không hơn.[…]
Hưởng thụ, hay chỉ trải qua? Kết quả khác nhau chính là sự mãn nguyện. Khi chỉ trải qua, chúng ta thường hay băn khoăn: Phải chăng đó đã là cái đẹp thực sự? Chuyến du ngoạn đáng giá? Bữa ăn đáng tiền? Phải chăng chiếc điện thoại đó là “đỉnh” nhất? Chiếc áo đó đã là đẹp nhất? Phải chăng ta đã có được thứ tương xứng với những gì ta bỏ ra? Những người thực sự hưởng thụ thì không băn khoăn, mà thường mãn nguyện. Những người thực sự tận hưởng hạnh phúc cũng vậy, họ mãn nguyện. Niềm vui đôi khi bị thúc đẩy bởi nhu cầu phải hét toáng lên cho cả thế gian. Nhưng sự mãn nguyện thường có khuôn mặt rất lặng lẽ, và hiếm khi phô trương.
Tôi nhận ra rằng để hưởng thụ thực sự, chúng ta cần phải học hỏi và có hiểu biết nhất định về điều ta đang làm, đang tận hưởng, đang thưởng thức. Biết mình có gì, hiểu thứ mình có, và biết cách tận hưởng tối đa những gì mình xứng đáng được hưởng, đó mới là hưởng thụ”.
(Phạm Lữ Ân, Nếu biết trăm năm là hữu hạn, tr.140)
Trả lời cho các câu 71, 72, 73, 74, 75 dưới đây:
Dòng nào dưới đây nêu đúng quan niệm của tác giả trong đoạn văn bản trên?
Đáp án đúng là: B
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: B
Ý nào dưới đây KHÔNG phải là quan niệm của tác giả?
Đáp án đúng là: D
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: D
Tác giả thuyết phục người đọc về quan điểm của mình chủ yếu bằng cách lập luận nào?
Đáp án đúng là: D
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: D
Giọng điệu tranh luận của tác giả trong đoạn trích là gì?
Đáp án đúng là: A
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: A
Tác giả của đoạn văn bản trên có viết tiếp rằng: “Ồ, cuộc đời cũng như hơi thở vậy thôi. Ta không thể hít một hơi dài quá khả năng của mình. Nhưng ta có thể hít sâu hết khả năng của mình trong từng hơi thở. Tôi vẫn tin rằng nếu bạn thực sự biết hưởng thụ, bạn sẽ luôn thấy mình đã sống rất sâu. Nếu biết trăm năm là hữu hạn, cớ gì ta không sống thật sâu…?”
Theo anh/chị, quan niệm “sống thật sâu” của người viết đoạn văn bản trên gần gũi nhất với quan niệm sống nào dưới đây?
Đáp án đúng là: C
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: C
Tác giả sử dụng các biện pháp tu từ nào trong hai câu thơ sau:
Thôn Đoài ngồi nhớ thôn Đông
Cau thôn Đoài nhớ giầu không thôn nào?
(Trích Tương tư, Nguyễn Bính)
Đáp án đúng là: D
Vận dụng kiến thức về biện pháp tu từ
Đáp án cần chọn là: D
Đọc đoạn thơ và trả lời câu hỏi dưới đây:
Các nhà khoa học đã chứng minh: Thái độ làm việc mới là yếu tố tiên quyết dẫn tới thành công trong công việc chứ không phải là mức độ thông minh.
Thái độ của con người thuộc một trong 2 trạng thái cốt lõi: nhận thức cố định (fixed mindset) và nhận thức phát triển (growth mind).
Đối với nhận thức cố định, bạn tin rằng bạn là ai và bạn không thể thay đổi. Do đó khi đối mặt với những thử thách mới, bạn sẽ cảm thấy rằng mọi thứ vượt quá tầm kiểm soát của bạn, từ đó dẫn tới cảm giác tuyệt vọng và bị choáng ngợp.
Những người có nhận thức phát triển lại tin rằng họ có thể cải thiện bằng sự nỗ lực. Họ làm việc hiệu quả hơn những người có nhận thức cố định ngay cả khi có chỉ số IQ thấp hơn họ chủ động nắm bắt thử thách, xem nó như một cơ hội để học được những thứ mới.
Người ta thường nghĩ rằng có khả năng, có sự thông minh sẽ truyền cảm hứng cho sự tự tin. Điều đó chỉ đúng đối với công việc diễn ra một cách suôn sẻ. Yếu tố quyết định trong cuộc sống là cách bạn xử lý những thất bại và thách thức. Những người có nhận thức phát triển sẽ dang rộng vòng tay để chào đón sự thất bại.
Theo giáo sư Dweck, sự thành công trong cuộc đời phụ thuộc vào cách bạn đối mặt với thất bại.
(Theo Chí Hiếu, Thái độ làm việc mới dẫn tới thành công chứ không phải thông minh)
Theo tác giả, những người có nhận thức phát triển so với những người có nhận thức cố định mang những nét khác biệt nào?
Đáp án đúng là: A
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: A
Câu ca dao sau muốn nói đến đối tượng nào?
Thương thay con cuốc giữa trời
Dầu kêu ra máu có người nào nghe.
Đáp án đúng là: A
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: A
Các từ láy trong đoạn trích sau có tác dụng gì?
Đêm mưa làm nhớ không gian,
Lòng run thêm lạnh nỗi hàn bao la...
Tai nương nước giọt mái nhà
Nghe trời nằng nặng, nghe ta buồn buồn.
Nghe đi rời rạc trong hồn
Những chân xa vắng dặm mòn lẻ loi...
(Trích Buồn đêm mưa, Huy Cận)
Đáp án đúng là: C
Căn cứ vào kiến thức về tù láy kết hợp đọc đoạn trích
Đáp án cần chọn là: C
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Ai cũng biết Hàn Quốc phát triển kinh tế khá nhanh, vào loại “con rồng nhỏ” có quan hệ khá chặt chẽ với các nước phương Tây, một nền kinh tế thị trường nhộn nhịp, có quan hệ quốc tế rộng rãi. Khắp nơi đều có quảng cáo, nhưng không bao giờ quảng cáo thương mại được đặt ở những nơi công sở, hội trường lớn, danh lam thắng cảnh. Chữ nước ngoài, chủ yếu là tiếng Anh, nếu có thì viết nhỏ đặt dưới chữ Triều Tiên to hơn ở phía trên. Đi đâu, nhìn đâu cũng thấy nổi bật những bảng hiệu chữ Triều Tiên. Trong khi đó thì ở một vài thành phố của ta nhìn vào đâu cũng thấy tiếng Anh, có bảng hiệu của các cơ sở của ta hẳn hoi mà chữ nước ngoài lại lớn hơn cả chữ Việt, có lúc ngỡ ngàng tưởng như mình lạc sang một nước khác.
Báo chí ở Hàn Quốc khá nhiều. Tôi không biết chữ Triều Tiên nhưng cũng xem qua khá nhiều tờ báo. Có một số tờ báo, tạp chí, số báo xuất bản bằng tiếng nước ngoài, in rất đẹp. Nhưng các tờ báo phát hành ở trong nước đều không có mấy trang viết bằng tiếng nước ngoài, trừ một số tạp chí khoa học, ngoại thương có in cuối mục lục bằng tiếng nước ngoài để người đọc nước ngoài nhờ dịch những bài cần đọc. Trong khi đó ở ta, khá nhiều báo, kể cả một số tờ báo của các ngành của nhà nước ta có cái “mốt” là tóm tắt một số bài chính bằng tiếng nước ngoài ở trang cuối, xem ra để cho “oai” trong khi đó người đọc trong nước lại bị thiệt mất mấy trang thông tin.
Phải chăng, đó cũng là thái độ tự trọng của một quốc gia khi mở cửa với bên ngoài, mà ta nên suy ngẫm.
(trích Bản lĩnh Việt Nam của Hữu Thọ)
Cụm từ “thái độ tự trọng” (in đậm) diễn tả điều gì?
Đáp án đúng là: B
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi
Đáp án cần chọn là: B
Từ “huyền thoại” (in đậm) trong câu sau được hiểu là gì?
Cần chuẩn bị những cái cần thiết trong hành trang mang vào thế kỉ mới, trong khi chúng ta đã chứng kiến sự phát triển như huyền thoại của khoa học và công nghệ.
(Vũ Khoan, Chuẩn bị hành trang vào thế kỉ mới)
Đáp án đúng là: B
Đọc kĩ nội dung đoạn trích đối chiếu với câu hỏi, suy luận nghĩa của từ
Đáp án cần chọn là: B
Đọc đoạn trích và trả lời câu hỏi dưới đây:
“Con sông Đà gợi cảm. Đối với mỗi người, sông Đà gợi một cách. Đã có lần tôi nhìn sông Đà như một cố nhân. Chuyến ấy ở rừng đi núi cũng đã hơi lâu, đã thấy thèm chỗ thoáng. Mải bám gót anh liên lạc, quên đi mất là mình sắp đổ ra sông Đà. Xuống một cái dốc núi, trước mắt thấy loang loáng như trẻ con nghịch chiếu gương vào mắt mình rồi bỏ chạy. Tôi nhìn cái miếng sáng loé lên một màu nắng tháng Ba Đường thi “Yên hoa tam nguyệt há Dương Châu”. Bờ sông Đà, bãi sông Đà, chuồn chuồn, bươm bướm trên sông Đà. Chao ôi, trông con sông, vui như thấy nắng giòn tan sau kì mưa dầm, vui như nối lại chiêm bao đứt quãng. Đi rừng dài ngày rồi lại bắt ra sông Đà, đúng thế, nó đằm đằm, ấm ấm như gặp lại cố nhân, mặc dù người cố nhân ấy mình biết là lắm bệnh lắm chứng, chốc dịu dàng đấy, rồi chốc lại bẳn tính và gắt gỏng thác lũ ngay đấy”
(Nguyễn Tuân, Người lái đò sông Đà)
Cảm xúc chủ yếu của nhân vật “tôi” trong đoạn văn trên là gì?
Đáp án đúng là: B
Phân tích, suy luận, cảm nhận
Đáp án cần chọn là: B
Câu ca dao sau diễn tả tâm trạng gì của nhân vật trữ tình?
Em tưởng nước giếng sâu em nối sợi gầu dài
Ai ngờ nước giếng cạn em tiếc hoài sợi dây.
Đáp án đúng là: A
Phân tích, suy luận, cảm nhận
Đáp án cần chọn là: A
Đọc đoạn trích và trả lời câu hỏi dưới đây:
Sau phút bối rối, ông Phúc dằn giọng:
- Nhưng tại ai? Bà không thấy làm thế là độc ác à?
Bà Son nhìn trân trân:
- Nhưng ông ấy là chồng tôi!
(Trích “Mảnh đất lắm người nhiều ma” – Nguyễn Khắc Trường)
Dòng nào nêu đúng hàm ý của câu văn in đậm trong đoạn trích trên:
Đáp án đúng là: C
Đọc kĩ đoạn trích, suy luận
Đáp án cần chọn là: C
Đọc đoạn thơ và trả lời câu hỏi dưới đây:
Trời lại mưa lâm thâm
Gió xoay chiều rét dữ
Bên cầu, em thấy chứ
Anh vẫn hành quân
(Trích Anh vẫn hành quân, Trần Hữu Thung)
Nghĩa của từ “mưa lâm thâm” là gì?
Đáp án đúng là: A
Vận dụng kiến thức về nghĩa của từ, kết hợp đọc thật kĩ văn bản
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 86 đến 90:
Nhưng trên thực tế, khoảng 80% nhà tuyển dụng tại Việt Nam than phiền rằng nhân viên trẻ quá yếu trong giao tiếp, không đáp ứng được công việc dù bằng cấp tốt. Tiến sĩ Nguyễn Thị Hoa- Viện Tâm lí học Việt Nam nhận định, phần đông người Việt thường mắc lỗi lớn nhất là giao tiếp một chiều, chỉ giao mà không tiếp. Nghĩa là chỉ nói và truyền đi mà không lắng nghe hoặc tiếp nhận thông tin phản hồi.
Một lỗi khác là giao tiếp quá chú trọng vào con người mà không để tâm đến mục đích giao tiếp, dẫn đến hiện tượng nói tràng giang đại hải, đang nói vấn đề này lại chen vào vấn đề khác làm cho người nghe không thể hiểu nổi hoặc chưa đi vào mục tiêu vấn đề đã vội chỉ trích cá nhân gây “phản ứng tự vệ”. Người nghe cũng thế, chưa kịp nhận thức vấn đề nhưng thấy ai bàn về vấn đề của mình thì vội vàng “tự vệ”.
Chính sự yếu kém trong giao tiếp này đã khiến không ít người Việt gặp khó khăn trong cuộc sống xã hội. Không hiếm các bạn trẻ học rất chăm, có nhiều bằng cấp, chứng chỉ tốt song không thể xin nổi việc vì trả lời “chẳng đâu vào đâu” câu hỏi phỏng vấn của các nhà tuyển dụng. Một số em vì thiếu kĩ năng giao tiếp còn không thể hòa đồng với xã hội ngay từ khi còn trên ghế nhà trường.
(Trích Kĩ năng giao tiếp của giới trẻ Việt Nam: đừng ở mức chỉ “giao” thiếu “tiếp”, Uyên Minh)
Trả lời cho các câu 86, 87, 88, 89, 90 dưới đây:
Đoạn trích trên sử dụng những phương thức biểu đạt nào?
Đáp án đúng là: A
Vận dụng kiến thức về phương thức biểu đạt
Đáp án cần chọn là: A
Nội dung chính của đoạn trích trên là gì?
Đáp án đúng là: C
Đọc đoạn trích, phân tích, tổng hợp
Đáp án cần chọn là: C
Đoạn trích thể hiện thái độ gì của tác giả?
Đáp án đúng là: B
Đọc đoạn trích, phân tích, tổng hợp
Đáp án cần chọn là: B
Ý nào sau đây KHÔNG phải là những hậu quả do mắc lỗi giao tiếp được nhắc đến trong đoạn trích?
Đáp án đúng là: D
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: D
Ý nào sau đây KHÔNG phải là những lỗi giao tiếp được nhắc đến trong đoạn trích?
Đáp án đúng là: C
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: C
Đọc đoạn trích dưới đây và trả lời câu hỏi từ 91 đến 95:
Những chiếc giỏ xe chở đầy hoa phượng
Em chở mùa hè của tôi đi đâu ?
Chùm phượng vĩ em cầm là tuổi tôi mười tám
Thuở chẳng ai hay thầm lặng - mối tình đầu
Mối tình đầu của tôi có gì ?
Chỉ một cơn mưa bay ngoài cửa lớp
Là áo người trắng cả giấc ngủ mê
Là bài thơ cứ còn hoài trong cặp
Giữa giờ chơi mang đến lại.... mang về.
(Trích Chút tình đầu- Đỗ Trung Quân)
Trả lời cho các câu 91, 92, 93, 94, 95 dưới đây:
Ý nào sau đây xác định đúng nhân vật trữ tình của đoạn thơ trên?
Đáp án đúng là: B
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: B
Ý nào sau đây nêu đúng cảm xúc của nhân vật trữ tình trong câu thơ “Giữa giờ chơi mang đến lại … mang về”?
Đáp án đúng là: B
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: B
Ý nào sau đây nêu đúng các biện pháp tu từ được sử dụng trong đoạn thơ?
Đáp án đúng là: C
Căn cứ vào các biện pháp nghệ thuật đã học
Đáp án cần chọn là: C
Ý nào sau đây nêu đúng ý nghĩa biểu tượng của hình ảnh “hoa phượng” trong đoạn thơ?
Đáp án đúng là: B
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: B
Ý nào sau đây nêu đúng nhất nội dung của đoạn thơ trên?
Đáp án đúng là: B
Đọc đoạn trích, đối chiếu câu hỏi với đoạn trích
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 96 đến 100:
Có lính huyện mang trát quan về làng :
Quan tri huyện huyện X.X.
Sức hương lí xã Ngũ Vọng tuân cử.
Nay thừa lệnh Tỉnh đường, ngày 19 Mars này, tức 29 tháng Giêng An Nam, tại sân vận động huyện có cuộc đá bóng thi, nhiều chiến tướng đá rất hay, mọi nhẽ.
Vậy sức các thầy phải thông báo cho dân làng biết và phải thân dẫn đủ một trăm người, đúng 12 giờ trưa đến xem, không được khiếm diện.
Những người đã cắt đi dự cuộc khánh thành sân thể dục tháng trước, thì lần này được miễn.
Ai có mặt tại sân vận động cũng phải ăn mặc tử tế, đi đứng nghiêm chính, và phải vỗ tay luôn luôn, vì hôm ấy có nhiều quan khách.
Làng Ngũ Vọng lại phải có năm lá cờ, sẵn sàng từ 10 giờ sáng.
Việc này tuy là việc thể dục, nhưng các thầy không được coi thường, nếu không tuân lệnh sẽ bị cữu.
Nay sức
Lê Thăng
(Trích "Tinh thần thể dục", Nguyễn Công Hoan)
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Trát quan trong đoạn trích thuộc phong cách ngôn ngữ nào?
Đáp án đúng là: D
Vận dụng kiến thức đã học về các phong cách ngôn ngữ
Đáp án cần chọn là: D
Xác định các từ, cụm từ KHÔNG thuộc phong cách ngôn ngữ hành chính, công vụ trong đoạn trích.
Đáp án đúng là: B
Vận dụng kiến thức đã học về các phong cách ngôn ngữ
Đáp án cần chọn là: B
Dòng nào sau đây nêu đúng giọng điệu chủ đạo của đoạn trích?
Đáp án đúng là: A
Đọc văn bản, phân tích, cảm nhận
Đáp án cần chọn là: A
Có thể xếp các từ, cụm từ “Này, tức 29 tháng Giêng An Nam, rất hay, mọi nhẽ, phải thân dẫn đủ, cũng phải ăn mặc tử tế, đi đứng nghiêm chỉnh, và phải vỗ tay luôn luôn, việc này tuy là… nhưng không được coi thường, nếu không… sẽ bị…” vào kiểu ngôn ngữ nào?
Đáp án đúng là: B
Vận dụng kiến thức về ngôn ngữ nói và ngôn ngữ viết
Đáp án cần chọn là: B
Theo đoạn trích, từ cữu (in đậm) có ý nghĩa gì?
Đáp án đúng là: C
Căn cứ vào nội dung của tác phẩm và kiến thức về nghĩa của từ
Đáp án cần chọn là: C