Cho hàm số $y = f(x)$ liên tục và có bảng biến thiên trên đoạn $\left\lbrack {- 1;3} \right\rbrack$ như hình vẽ. Tìm giá trị nhỏ nhất cuả hàm số trên đoạn $\left\lbrack {- 1;3} \right\rbrack$.
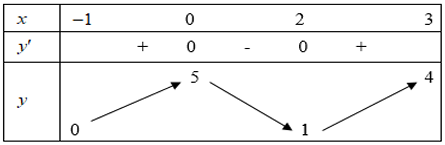
Đáp án đúng là: B
Quan sát BBT và nhận xét
Đáp án cần chọn là: B
Đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{x + 1}{x - 2}$ là
Đáp án đúng là: C
Xét mẫu số bằng 0 tìm tiệm cận đứng
Đáp án cần chọn là: C
Cho hàm số $y = f(x)$ có bảng biến thiên trên $\left( {- 3;5} \right\rbrack$ như sau:
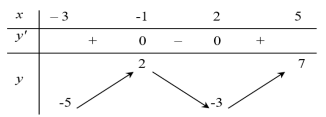
Giá trị cực tiểu của hàm số đã cho bằng
Đáp án đúng là: D
Quan sát BBT và nhận xét
Đáp án cần chọn là: D
Hàm số nào dưới đây đồng biến trên $\mathbb{R}$?
Đáp án đúng là: A
Hàm số đồng biến khi $f'(x) > 0$
Đáp án cần chọn là: A
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
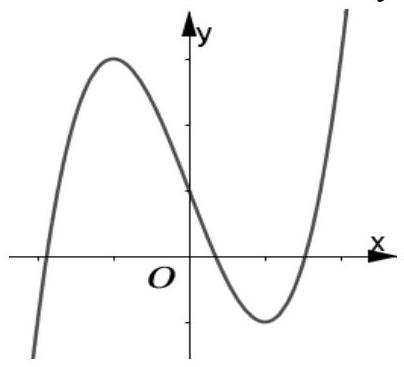
Đáp án đúng là: D
Dựa vào hình dạng đồ thị, tính đơn điệu và các điểm mà đồ thị đi qua để tìm hàm số
Đáp án cần chọn là: D
Giá trị lớn nhất của hàm số $f(x) = x^{3} - 3x^{2} - 9x + 10$ trên đoạn $\left\lbrack {- 2;2} \right\rbrack$ bằng
Đáp án đúng là: D
Tính đạo hàm và khảo sát trên đoạn $\left\lbrack {- 2,2} \right\rbrack$
Đáp án cần chọn là: D
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
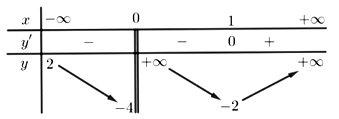
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Đáp án đúng là: A
Quan sát BBT và các giới hạn
Đáp án cần chọn là: A
Đường cong trong hình là đồ thị của hàm số nào dưới đây?
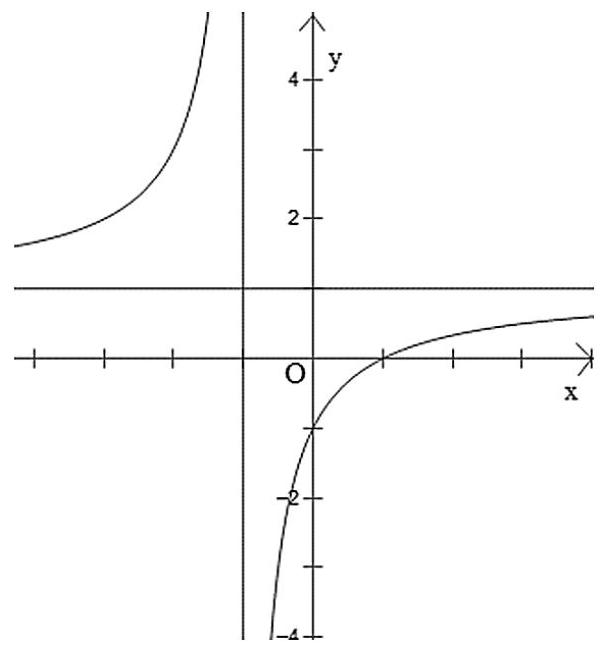
Đáp án đúng là: A
Đựa vào hình dáng đồ thị và các đường tiệm cận
Đáp án cần chọn là: A
Cho hàm số $y = f(x)$ xác định với mọi $x \neq - 6$ và có bảng xét dấu $f'(x)$ như hình vẽ dưới đây. Hàm số đồng biến trên khoảng nào trong các khoảng sau?

Đáp án đúng là: D
Hàm số đồng biến khi $f'(x) > 0$
Đáp án cần chọn là: D
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
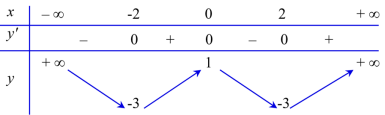
Số nghiệm của phương trình \(f\left( x \right) = 1\) là
Đáp án đúng là: D
Tương giao đồ thị.
Đáp án cần chọn là: D
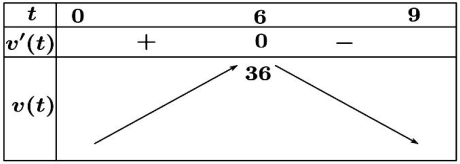
Một vật chuyển động theo quy luật \(s(t)=-\dfrac{1}{3} t^3+6 t^2\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \(s\) (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Đáp án đúng là: D
Đáp án cần chọn là: D
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {{x^2} + x - 2} \right)\left( {x - 1} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
Đáp án đúng là: D
Điểm cực trị của hàm số là điểm f’(x) đi qua đổi dấu
Là nghiệm đơn hoặc nghiệm bội lẻ của phương trình \(f'\left( x \right) = 0\)
Đáp án cần chọn là: D
Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
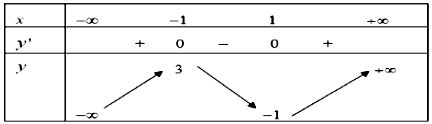
| Đúng | Sai | |
|---|---|---|
| a) Hàm số có giá trị cực đại bằng 3. | ||
| b) Hàm số có hai điểm cực trị. | ||
| c) Hàm số đạt cực đại tại điểm $x = 1$. | ||
| d) Hàm số có hai giá trị cực trị là -1 và 1. |
Đáp án đúng là: Đ; Đ; S; S
Quan sát BBT và nhận xét các điểm cực trị và GTLN, GTNN
Đáp án cần chọn là: Đ; Đ; S; S
Hàm số $y = f(x)$ có đồ thị như hình vẽ bên dưới.
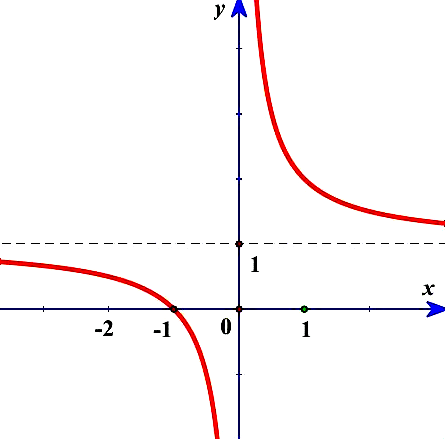
| Đúng | Sai | |
|---|---|---|
| a) Điểm $\left( {0;1} \right)$ là tâm đối xứng của đồ thị hàm số $y = f(x)$. | ||
| b) Hàm số $y = f(x)$ đồng biến trong khoảng $\left( {- \infty;0} \right)$ và $\left( {0; + \infty} \right)$. | ||
| c) Hàm số $y = f(x)$ có hai điểm cực trị. | ||
| d) Đồ thị hàm số $y = f(x)$ có một tiệm cận đứng và một tiệm cận ngang. |
Đáp án đúng là: Đ; S; S; Đ
Nhận dạng đồ thị từ các đường tiệm cận, tính đơn điệu và các điểm mà đồ thị đi qua
Đáp án cần chọn là: Đ; S; S; Đ
Cho hàm số $y = \dfrac{x^{2} + 6x + 11}{x + 2}$. Xét tính đúng-sai của các khẳng định sau
| Đúng | Sai | |
|---|---|---|
| a) Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình $x = - 2$. | ||
| b) $y' = \dfrac{x^{2} + 4x + 1}{{(x + 2)}^{2}}$. | ||
| c) Phương trình $y' = 0$ có 2 nghiệm phân biệt. | ||
| d) Tiệm cận xiên của đồ thị hàm số là đường thẳng có phương trình $y = x + 4$. |
Đáp án đúng là: Đ; Đ; Đ; Đ
Tính đạo hàm, giải phương trình $y' = 0$ và tìm các đường tiệm cận của hàm số
Đáp án cần chọn là: Đ; Đ; Đ; Đ
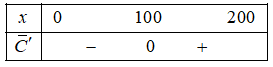
Trong một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất $x$ m3 nước tinh khiết thì phải chi trả các khoản sau: 5 triệu đồng chi phí cố định; 0,15 triệu đồng cho mỗi mét khối sản phẩm; $0,0005x^{2}$ chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là $200m^{3}$. Gọi $C(x)$ là chi phí sản xuất $x$ ($m^{3}$) sản phẩm mỗi ngày và $\overline{C}(x)$ là chi phí trung bình mỗi mét khối sản phẩm. Khi đó:
| Đúng | Sai | |
|---|---|---|
| a) $C(x) = 0,0005x^{2} + 0,15x + 5$ | ||
| b) Chi phí sản xuất $100\text{m}^{3}$ nước tinh khiết là 20 triệu đồng | ||
| c) Chi phí trung bình giảm xuống khi sản lượng nước tinh khiết trong ngày không vượt quá $100\text{m}^{3}$ | ||
| d) $\overline{C}(x) = 0,0005x + 0,15 + \dfrac{5}{x}$ |
Đáp án đúng là: Đ; S; Đ; Đ
Đáp án cần chọn là: Đ; S; Đ; Đ
Cho hàm số $y = \dfrac{2x^{2} + 5x + 5}{x + 1}$. Gọi $\text{Δ}$ là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số. Khoảng cách từ gốc tọa độ $O$ đến $\text{Δ}$ là bao nhiêu (Kết quả làm tròn đến hàng thập phân thứ hai).
Đáp án đúng là:
Phương trình qua 2 điểm cực trị có dang $y = \dfrac{(2x + 5x + 5)'}{\left( {x + 1} \right)'}$
Áp dụng công thức tính khoảng cách từ 1 điểm đến 1 đường thẳng
Đáp án cần điền là: 1,21
Gọi \(m, M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hảm số \(f(x)=\dfrac{1}{2} x-\sqrt{x+1}\) trên doạn \([0 ; 3]\). Tổng \(S=2 M-m\) bằng bao nhiêu?
Đáp án đúng là:
Đáp án cần điền là: 0
Ta xác định được các số $a, b, c$ để đồ thị hàm số $y=x^3+a x^2+b x+c$ đi qua điểm $(1 ; 0)$ và có điểm cực trị $(-2 ; 0)$. Tính giá trị biểu thức $T=a^2+b^2+c^2$.
Đáp án đúng là:
Đáp án cần điền là: 25
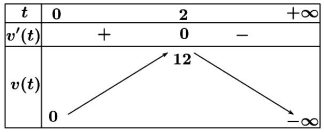
Một chất điểm chuyển động theo quy luật \(S(t)=6 t^2-t^3\). Vận tốc \(v(\mathrm{~m} / \mathrm{s})\) của chuyển động đạt giá trị lớn nhất tại thời điểm \(t(\mathrm{~s})\) bằng bao nhiêu giây?
Đáp án đúng là:
Đáp án cần điền là: 2
Một cốc chứa 25 ml dung dịch NaOH với nồng độ \(100 \mathrm{mg} / \mathrm{ml}\). Một bình chứa dung dịch NaOH khác với nồng độ \(9 \mathrm{mg} / \mathrm{ml}\) được trộn vào cốc. Gọi \(C(x)\) là nồng độ của NaOH sau khi trộn \(x\) \((\mathrm{ml})\) từ bình chứa, ta thấy nồng độ của NaOH trong cốc sẽ luôn giảm theo \(x\) nhưng luôn lớn hơn một số \(a\). Tính \(a\) ?
Đáp án đúng là:
Đáp án cần điền là: 9
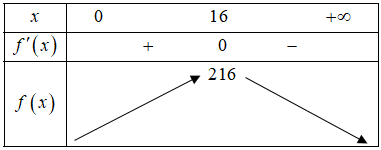
Một trang sách có dạng hình chữ nhật với diện tích là $384\text{cm}^{2}$. Sau khi để lề trên và lề dưới đều là 3 cm để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Phần in chữ trên trang sách có diện tích lớn nhất bằng bao nhiêu?
Đáp án đúng là:
Gọi trang sách hình chữ nhật có chiều dài là $x$ với $x > 0$, cm.
Tính chiều rộng, diện tích phần in chữ theo $x$ và khảo sát hàm số tìm GTLN
Đáp án cần điền là: 216