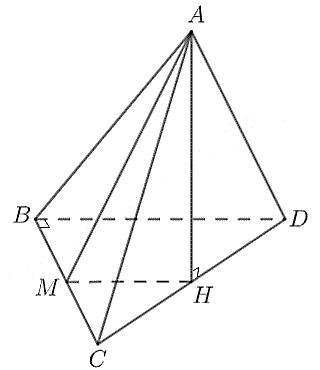
Phần 1: Toán học và xử lý số liệu
Cho cấp số nhân $\left( u_{n} \right)$ thỏa mãn $2\left( {u_{3} + u_{4} + u_{5}} \right) = u_{6} + u_{7} + u_{8}$. Tính $\dfrac{u_{8} + u_{9} + u_{10}}{u_{2} + u_{3} + u_{4}}$
Đáp án đúng là: 4
Sử dụng công thức $u_{n} = u_{k}q^{n - k}$
Đáp án cần điền là: 4
Trên hai tia \(Ox\), \(Oy\) của góc nhọn \(xOy\)lần lượt cho \(5\) điểm và \(6\) điểm phân biệt khác \(O\). Chọn ngẫu nhiên \(3\) điểm từ \(12\) điểm (gồm điểm \(O\) và \(11\) điểm đã cho), xác suất để \(3\) điểm chọn được là ba đỉnh của một tam giác bằng
Đáp án đúng là: C
3 điểm không thẳng hàng tạo thành 1 tam giác
Đáp án cần chọn là: C
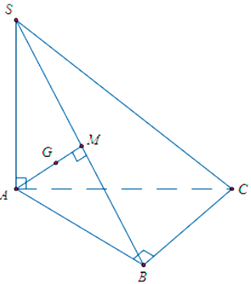
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt đáy và $SA = AB = \sqrt{3}$. Gọi $G$ là trọng tâm của tam giác SAB. Khoảng cách từ $G$ đến mặt phẳng $(SBC)$ bằng:
Đáp án đúng là: B
Gọi $M$ là trung điểm của SB. Chứng minh $GM\bot(SBC)$.
Khi đó, $d(G;(SBC)) = GM$.
Tính khoảng cách từ một điểm đến một mặt phẳng.
Đáp án cần chọn là: B
Số giá trị nguyên của tham số $m \in \lbrack - 30;30\rbrack$ sao cho đồ thị hàm số $y = \dfrac{2x^{2} + 5}{x^{3} + (m - 4)x + 2m}$ có ít nhất một tiệm cận đứng nằm bên phải trục tung là?
Đáp án đúng là: C
Để đồ thị hàm số có ít nhất một tiệm cận đứng nằm bên phải trục tung thì phương trình $x^{3} + (m - 4)x + 2m = 0$ có ít nhất 1 nghiệm dương.
Đáp án cần chọn là: C
Cho hình chóp S.ABCD có thể tích V. Gọi M, N lần lượt là trung điểm của SA, MC. Thể tích của khối chóp N.ABCD là
Đáp án đúng là: C
Tính tỉ lệ chiều cao của hai khối chóp, từ đó suy ra tỉ lệ thể tích.
Đáp án cần chọn là: C
Tập nghiệm của bất phương trình $2^{x} > 6$ là
Đáp án đúng là: A
Giải bất phương trình mũ.
Đáp án cần chọn là: A
Tại một thành phố, nhiệt độ ngoài trời vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức $h(t) = 29 + 3\sin\dfrac{\pi}{12}(t - 9)$ với $h$ tính bằng ${}^{{^\circ}}C$ và $t$ là thời gian trong ngày tính bằng giờ. Thời gian nhiệt độ cao nhất trong ngày là:
Đáp án đúng là: B
Sử dụng tập giá trị của hàm số sin để tìm nhiệt độ cao nhất trong ngày.
Giải điều kiện để tìm thời gian nhiệt độ cao nhất.
Đáp án cần chọn là: B
Cho các số nguyên $\text{a},\text{b},\text{c}$ thỏa mãn $a + \dfrac{b + \log_{2}5}{c + \log_{2}3} = \log_{6}45$. Tổng $a + b + c$ bằng
Đáp án đúng là: 1
Sử dụng các công thức:
$\log_{a}b = \dfrac{\log_{c}b}{\log_{c}a}(0 < a,c \neq 1,b > 0)$
$\log_{a}(xy) = \log_{a}x + \log_{a}y\,\,(0 < a \neq 1,x,y > 0)$
$\log_{a^{n}}b^{m} = \dfrac{m}{n}\log_{a}b\,\,(0 < a \neq 1,b > 0)$
Đáp án cần điền là: 1
Từ vị trí $A$, người ta quan sát một cây cao (tham khảo hình vẽ). Biết $AH = 4$m, $HB = 20$m, $\widehat{BAC} = 45^{0}$. Chiều cao của cây bằng bao nhiêu mét? Kết quả lấy sau dấu phẩy một chữ số.
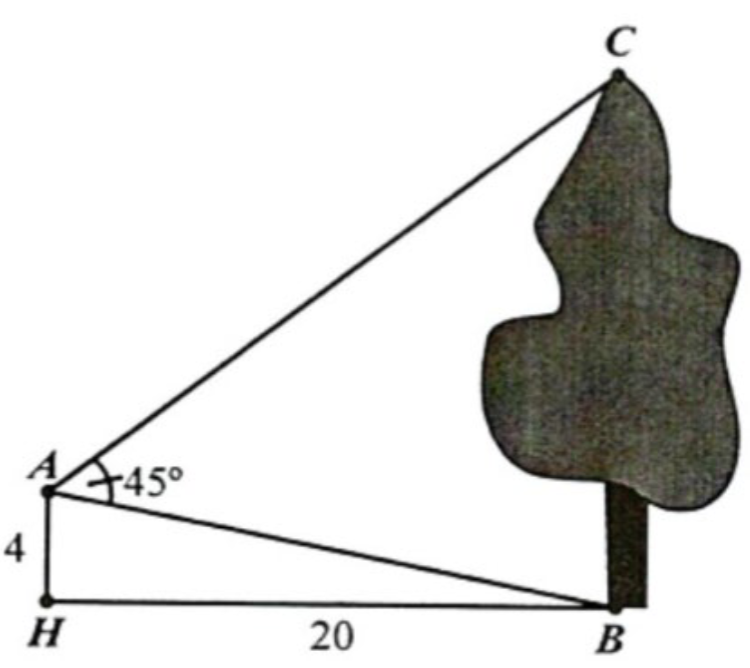
Đáp án đúng là: C
Hệ thức lượng trong tam giác và định lý sin $\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$
Đáp án cần chọn là: C
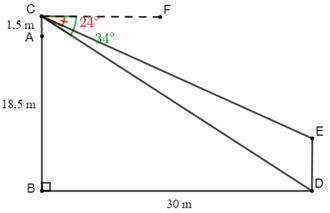
Từ trên nóc của một tòa nhà cao 18,5m, bạn Nam quan sát một cái cây cách tòa nhà 30m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Đáp án đúng là: 6,9
Giả sử toà nhà là AB = 18,5m; giác kế AC = 1,5m; chiều cao của cái cây là DE; khoảng cách từ tòa nhà tới cây là BD = 30m.
Góc tạo bởi phương quan sát gốc cây và phương nằm ngang là \(\widehat {FCD} = {34^0}\), góc tạo bởi phương quan sát ngọn cây và phương nằm ngang là \(\widehat {FCE} = {24^0}\).
Ta cần tính DE.
Đáp án cần điền là: 6,9
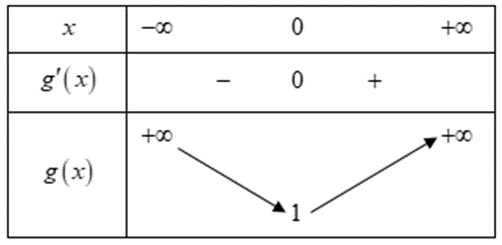
Cho phương trình $e^{x} = \ln(x + a) + a$, với $a$ là tham số. Có bao nhiêu giá trị nguyên của $a$ thuộc khoảng $(0;19)$ để phương trình có nghiệm dương.
Đáp án đúng là: 17
- Biến đổi đưa phương trình về dạng hàm đặc trưng dạng $a = g(x)$
- Khảo sát hàm số $g(x)$ để tìm điều kiện của $a$.
Đáp án cần điền là: 17
Cho đồ thị hàm số lượng giác như hình vẽ:
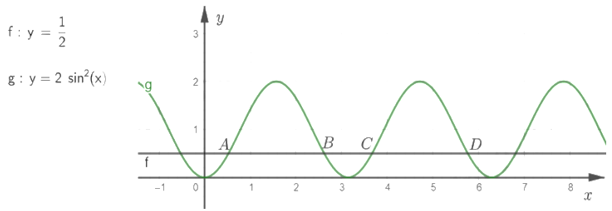
Đường thẳng $y = \dfrac{1}{2}$ cắt đồ thị hàm số $y = 2\sin^{2}x$ tại 4 điểm A, B, C, D như hình vẽ. Giá trị của $x_{B} + x_{D}$ là $\dfrac{a}{b}\pi$. Biết $\dfrac{a}{b}$ là phân số tối giản. Giá trị của $2a + b$ là:
Đáp án đúng là: 19
Giải phương trình hoành độ giao điểm tìm $x_{B};x_{D}$. Từ đó tính giá trị $x_{B} + x_{D}$.
Đáp án cần điền là: 19
Biết bất phương trình $\log_{2}\left( {3^{x} - 3} \right)\log_{8}\left( {3^{x}2^{- 2} - \dfrac{3}{4}} \right) \leq 1$ có tập nghiệm là đoạn [a; b]. Giá trị biểu thức $a + b$ bằng
Đáp án đúng là: B
Đặt ẩn $t = \log_{2}\left( {3^{x} - 3} \right)$
Đáp án cần chọn là: B
Một chiếc cổng parabol dạng $y = - \dfrac{1}{2}x^{2}$ có chiều rộng $d = 8m$. Hỏi chiều cao của chiếc cổng là?
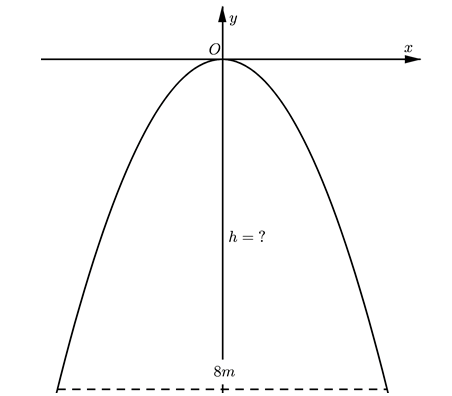
Đáp án đúng là: 8
Tìm tọa độ chân cổng. Từ đó ta có chiều cao cổng bằng trị tuyệt đối trung độ chân cổng.
Đáp án cần điền là: 8
Cho $\text{a},\text{b},\text{c}$ là ba số thực dương, $a > 1$ thỏa mãn
$\log_{a}^{2}(bc) + \log_{a}\left( {b^{3}c^{3} + \dfrac{bc}{4}} \right)^{2} + 4 + \sqrt{9 - c^{2}} = 0$
Khi đó, giá trị của biểu thức $T = a + 3b + 2c$ gần với giá trị nào nhất sau đây?
Đáp án đúng là: A
Áp dụng bất đẳng thức ${(x + y)}^{2} \geq 4xy$
$\log_{a}^{2}(bc) + \log_{a}\left( {b^{3}c^{3} + \dfrac{bc}{4}} \right)^{2} + 4 + \sqrt{9 - c^{2}} \geq \left\lbrack {\log_{a}(bc) + 2} \right\rbrack^{2} + \sqrt{9 - c^{2}} \geq 0$
Xét điều kiện để dấu “=” xảy ra.
Đáp án cần chọn là: A
Cho cấp số cộng $\left( u_{n} \right)$ có $u_{1} = 4$. Giá trị nhỏ nhất của $u_{1}u_{2} + u_{2}u_{3} + u_{3}u_{1}$ bằng:
Đáp án đúng là: A
Sử dụng công thức số hạng tổng quát của cấp số cộng: $u_{n} = u_{1} + (n - 1)d$
Tính biểu thức $u_{1}u_{2} + u_{2}u_{3} + u_{3}u_{1}$ theo $d$ rồi tìm giá trị nhỏ nhất.
Đáp án cần chọn là: A
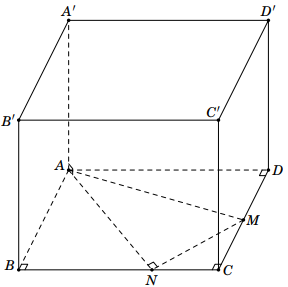
Cho hình hộp chữ nhật $ABCD \cdot A'B'C'D'$ có $AB = 6$, $AD = 9$. Lấy M là trung điểm của CD, N thuộc cạnh BC sao cho $NB = 2NC$. Khoảng cách giữa hai đường thẳng $AA'$ và MN bằng $a\sqrt{2}$, tìm $a.$
Đáp án đúng là: 6
Đáp án cần điền là: 6
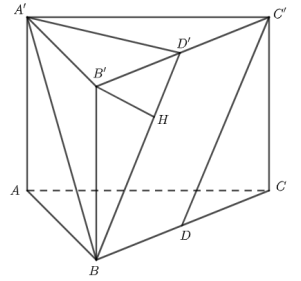
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy ABC là tam giác đều cạnh $a$. Gọi $D$ là trung điểm cạnh BC. Biết $AA' = 2a$, khoảng cách giữa hai đường thẳng $A'B$ và $C'D$ là:
Đáp án đúng là: A
Gọi $D'$ là trung điểm của $B'C'$.
Kẻ $B'H\bot BD'$.
Chứng minh $d\left( {A'B;C'D} \right) = B'H$.
Sử dụng hệ thức lượng trong tam giác vuông để tính $B'H$.
Đáp án cần chọn là: A
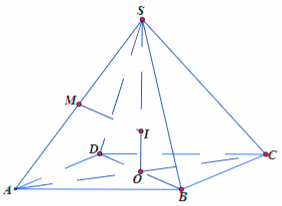
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên hợp với đáy một góc bằng $60^{o}$. Kí hiệu $V_{1}$, $V_{2}$ lần lượt là thể tích khối cầu ngoại tiếp, thể tích khối nón ngoại tiếp hình chóp đã cho. Tính tỉ số $\dfrac{V_{1}}{V_{2}}$.
Đáp án đúng là: A
Đáp án cần chọn là: A
Cho cấp số nhân $\left( u_{n} \right)$ có $u_{2} = - 6,u_{5} = 48$. Tính $S_{5}$.
Đáp án đúng là: C
Tính tổng n số hạng đầu tiên của dãy
Đáp án cần chọn là: C
Hai cậu bé cùng bắn bi vào lỗ. Xác suất người thứ nhất bắn trúng vào lỗ là 85%, xác suất người thứ hai bắn trúng vào lỗ là 75%. Hỏi xác suất để cả hai người cùng bắn trúng vào lỗ:
Đáp án đúng là: D
Sử dụng quy tắc nhân.
Đáp án cần chọn là: D
Trong mặt phẳng với hệ toạ độ Oxy, cho hai điểm A(1;1), B(-2;4) và đường thẳng \(\Delta :\,\,mx - y + 3 = 0.\) Tích tất cả các giá trị của tham số m để \(\Delta \) cách đều hai điểm A, B là? (nhập đáp án vào ô trống).
Đáp án đúng là: -1
\(\Delta \) cách đều A, B khi và chỉ khi \(\left[ \begin{array}{l}I \in \Delta \\\Delta //AB\end{array} \right.\).
Đáp án cần điền là: -1
Hàm số $y = 3\cos\left( {\dfrac{\pi}{4} - mx} \right)$ tuần hoàn có chu kì $T = 3\pi$ khi
Đáp án đúng là: B
Tìm chu kì của hàm số lượng giác
Đáp án cần chọn là: B
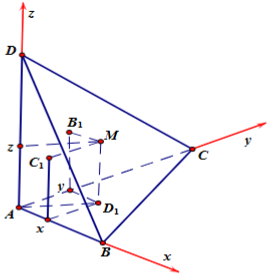
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và $AB = a$, $AC = 2a$, $AD = 3a.$ Gọi M là điểm thuộc miền trong của tam giác BCD, qua M kẻ các đường thẳng $d_{1},d_{2},d_{3}$ lần lượt song song với AB, AC, AD và cắt các mặt phẳng tương ứng $(ACD)$,$(ABD)$,$(ABC)$ tại $B_{1},C_{1},D_{1}$. Thể tích khối $MB_{1}C_{1}D_{1}$ lớn nhất bằng
Đáp án đúng là: C
Chọn $a = 1,$gắn hệ trục toạ độ.
Đáp án cần chọn là: C
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có A(1;2), b(0;3) và C(4;0). Chiều cao của tam giác kẻ từ đỉnh A bằng:
Đáp án đúng là: A
Viết phương trình đường thẳng BC.
Tính \({h_A} = d\left( {A,BC} \right).\)
Đáp án cần chọn là: A
Một vật chuyển động theo quy luật $s = - \dfrac{1}{2}t^{3} + 9t^{2}$ với $t$ (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và $s$ (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Đáp án đúng là: D
Vận tốc của vật là $v(t) = s'(t)$.
Tìm giá trị lớn nhất của $v(t)$.
Đáp án cần chọn là: D
Biểu đồ dưới đây thể hiện tỉ lệ lạm phát cơ bản bình quân năm trong giai đoạn 2018 – 2022:
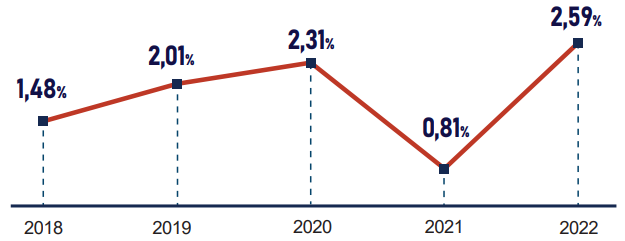
(Nguồn: Niêm giám thống kê 2022)
Trong giai đoạn từ 2018 – 2021, năm có tỉ lệ lạm phát cơ bản bình quân năm cao nhất là?
Đáp án đúng là: B
Nhìn biểu đồ.
Đáp án cần chọn là: B
Cho hình vuông OABC cạnh bằng 8, điểm M nằm trong hình vuông sao cho khoảng cách từ M đến các cạnh OA, OC cùng bằng 3. Parabol $\left( P_{1} \right)$ đi qua các điểm O, A, M, Parabol $\left( P_{2} \right)$ đi qua các điểm O, C, M. Tính diện tích phần tô đậm (hình vẽ bên).
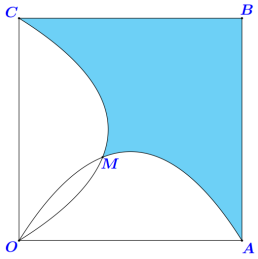
Đáp án đúng là: 95/3
Chọn hệ trục tọa độ Oxy sao cho tia Ox trùng tia OA, tia Oy trùng tia OC.
Chia hình thành các phần diện tích, ứng dụng tích phân để tính diện tích từng phần.
Đáp án cần điền là: 95/3
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số $y = {(x - 2)}^{2}(x + 1)$ là
Đáp án đúng là: A
- Tìm hai điểm cực trị.
- Áp dụng công thức khoảng cách giữa hai điểm $A\left( {x_{A};y_{A}} \right);B\left( {x_{B};y_{B}} \right)$:
$AB = \sqrt{\left( {x_{A} - x_{B}} \right)^{2} + \left( {y_{A} - y_{B}} \right)^{2}}$
Đáp án cần chọn là: A
Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là \(\dfrac{1}{5}\) và \(\dfrac{2}{7}\). Gọi \(A\) là biến cố: "Cả hai cùng ném bóng trúng vào rổ". Khi đó, xác suất của biến cố \(A\) là bao nhiêu?
Đáp án đúng là: D
\(A,B\) là hai biến cố độc lập nên: \(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right)\).
Đáp án cần chọn là: D
Số hạng không chứa x trong khai triển \({\left( {2x - \dfrac{1}{{{x^2}}}} \right)^6}\) là:
Đáp án đúng là: C
Khai triển nhị thức Niu-tơn: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} \).
Đáp án cần chọn là: C
Tìm các đường tiệm cận của đồ thị hàm số $y = \dfrac{\sqrt{x^{2} - 4}}{x - 1}$.
Đáp án đúng là: C
Xác định tiệm cận của đồ thị hàm số.
Đáp án cần chọn là: C
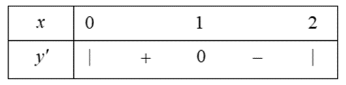
Cho hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ và $f'(x) < 0,\forall x \in (0; + \infty)$ biết $f(0) = 3$. Khẳng định nào sau đây có thể xảy ra:
Đáp án đúng là: D
Kiểm tra từng đáp án.
Đáp án cần chọn là: D
Chọn ngẫu nhiên lần lượt các số a, b phân biệt thuộc tập hợp $\left\{ {3^{k} \mid k \in N,1 \leq k \leq 10} \right\}$. Tính xác suất để $\log_{a}b$ là một số nguyên dương.
Đáp án đúng là: 17/90
Sử dụng công thức tính xác suất xảy ra biến cố $A:P(A) = \dfrac{n_{A}}{n_{\Omega}}$.
Đáp án cần điền là: 17/90
Cho hàm số $f(x) = k\sqrt[3]{x} + \sqrt{x}$. Với giá trị nào của $k$ thì $f'(1) = \dfrac{3}{2}$?
Đáp án đúng là: C
Tính đạo hàm của hàm số.
Từ đó tính $\left. f'(1)\Rightarrow k \right.$.
Đáp án cần chọn là: C
Cho hàm số $y = \sqrt{2x - x^{2}}$. Biết hàm số nghịch biến trên đoạn $(a;b)$. Tính $a + 2b$.
Đáp án đúng là: 5
Tìm tập xác định, khảo sát hàm số.
Đáp án cần điền là: 5
Cho các số thực $\text{a},\text{b},\text{c}$ thỏa mãn $c^{2} + a = 18$ và $\lim\limits_{x\rightarrow + \infty}\left( {\sqrt{ax^{2} + bx} - cx} \right) = - 2$. Tính giá trị biểu thức $P = a + b + 5c$.
Đáp án đúng là: C
Tính giới hạn hàm số.
Đáp án cần chọn là: C
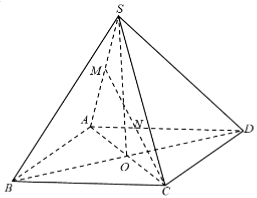
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng $SA = SC$, $SB = SD$. Khẳng định nào dưới đây đúng?
Đáp án đúng là: A
Quan hệ vuông góc trong không gian.
Đáp án cần chọn là: A
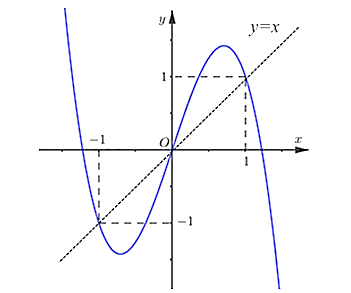
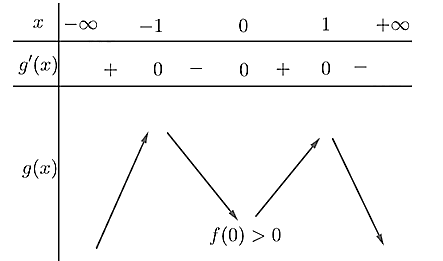
Cho hàm số $f(x)$ liên tục và có đạo hàm trên $\mathbb{R}$. Biết $f(0) > 0$. Đồ thị hàm số $y = f'(x)$ như hình vẽ:
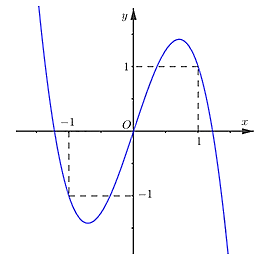
Hàm số $y = \left| {f(x) - \dfrac{x^{2}}{2}} \right|$ có bao nhiêu điểm cực trị?
Đáp án đúng là: B
Số điểm cực trị của $\left. y = \middle| f(x) \middle| = \right.$ Số điểm cực trị của $y = f(x) +$ Số nghiệm bội lẻ của $f(x) = 0$.
Đáp án cần chọn là: B
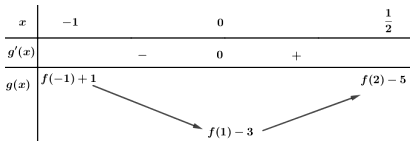
Cho hàm số $f(x)$, đồ thị của hàm số $y = f'(x)$ là đường cong như hình vẽ bên dưới.
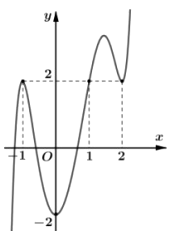
Giá trị nhỏ nhất của hàm số $g(x) = f\left( {2x + 1} \right) - 4x - 3$ trên đoạn $\left\lbrack {- 1;\dfrac{1}{2}} \right\rbrack$ bằng:
Đáp án đúng là: C
Tính đạo hàm của hàm $g'(x)$
Dựa vào đồ thị của hàm số $y = f'(x)$ để giải phương trình $g'(x) = 0$.
Lập bảng biến thiên tìm giá trị nhỏ nhất của hàm $g(x).$
Đáp án cần chọn là: C
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {y^2} - 4x - 6y - 12 = 0\). Gọi \(I\) là tâm và \(R\) là bán kính của \(\left( C \right)\). Gọi \(M\left( {a;\,b} \right),\,\,a > 0\) thuộc đường thẳng \(d:2x - y + 3 = 0\) sao cho \(MI = 2R\). Khi đó, giá trị của biểu thức \({a^2} + {b^2}\) là
Đáp án đúng là: C
- Xác định tọa độ tâm \(I\) và bán kính \(R\).
- Xác định tọa độ điểm \(M\left( {t;\,\,2t + 3} \right)\) và tính véc-tơ \(IM\).
- Sử dụng đề bài để tìm \(t\). Từ đó tính được giá trị của biểu thức \({a^2} + {b^2}\).
Đáp án cần chọn là: C
Cho tứ diện ABCD có BCD là tam giác vuông tại đỉnh $B$, cạnh $CD = a,BD = \dfrac{a\sqrt{6}}{3}$, $AB = AC = AD = \dfrac{a\sqrt{3}}{2}$. Tính cosin của góc nhị diện [A, BC, D].
Đáp án đúng là: 1/2
Xác định góc nhị diện [A, BC, D].
Đáp án cần điền là: 1/2
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
Đáp án đúng là: D
Xác định tứ phân vị thứ nhất, thứ ba và khoảng tứ phân vị.
Đáp án cần chọn là: D
Trên một đoạn đường, có 11 địa điểm bao gồm một trung tâm ở chính giữa và 10 nơi để tham quan, mua sắm; hai địa điểm cạnh nhau thì cách nhau 100 mét. Những người khách xuất phát từ trung tâm và muốn đi tham quan tổng cộng 3 lượt, mỗi lượt đi một nơi khác nhau (họ đến địa điểm đó tham quan sau đó quay về trung tâm và chuẩn bị cho lần đi tiếp theo). Hỏi có bao nhiêu cách chọn ra ba địa điểm, có thứ tự và không nhất thiết phân biệt, sao cho tổng quãng đường cả đi lẫn về không vượt quá 1 km?
Đáp án đúng là: 80
Bài toán chia kẹo Euler.
Bất phương trình ${\sum\limits_{i = 1}^{k}x_{i}} \leq n$ $(n \geq k)$ có $C_{n}^{k}$ nghiệm nguyên dương.
Đáp án cần điền là: 80
Cho hình phẳng $(H)$ giới hạn bởi đồ thị hàm số $y = 2x - x^{2}$ và trục hoành. Tính thể tích $V$ của vật thể tròn xoay sinh ra khi cho $(H)$ quay xung quanh trục Ox.
Đáp án đúng là: A
Ứng dụng của tích phân tính thể tích khối tròn xoay.
Đáp án cần chọn là: A
Tìm tất cả các giá trị của tham số $m$ để bất phương trình $x^{2} - (m + 2)x + 8m + 1 \leq 0$ vô nghiệm.
Đáp án đúng là: B
Dấu của tam thức bậc hai: $\left. ax^{2} + bx + c > 0,\forall x \in {\mathbb{R}}\Leftrightarrow\left\{ {\begin{array}{l} {a > 0} \\ {\Delta < 0} \end{array}.} \right. \right.$
Đáp án cần chọn là: B
Năng lượng giải tỏa $E$ của một trận động đất tại tâm địa chấn $M$ độ Richter được xác định bởi công thức $\log E = 11,4 + 1,5M$. Vào năm 1995 , thành phố $X$ xảy ra một trận động đất 8 độ Richter và năng lượng giải tỏa tại tâm địa chấn của nó gấp 14 lần trận động đất ra tại thành phố $Y$ vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố $Y$ là $\overline{a,2}$. Giá trị của $a$ là?
Đáp án đúng là: 7
Từ tỉ lệ năng lượng tỏa ra của 2 trận động đất suy ra độ lớn của trận động đất tại thành phố $Y$.
Đáp án cần điền là: 7
Một khu bảo tồn động vật thực hiện thống kê số lượng hươu trong khu vực vào ngày 31 tháng 12 hàng năm. Năm 2016 thống kê được số hươu là 150 con, đến năm 2021 số hươu là 360 con. Giả sử, số lượng hươu tính được xác định xấp xỉ theo hàm số mũ $P = P_{0} \cdot \text{e}^{kt}$, trong đó $k$ là hằng số, $P_{0}$ là số hươu tại thời điểm năm 2016, $P$ là số hươu tại thời điểm $t$ tính từ thời điểm gốc ($t$ tính theo đơn vị năm).
Trả lời cho các câu 48, 49, 50 dưới đây:
Số con hươu tại khu bảo tồn được thống kê vào ngày 31 tháng 12 năm 2024 là
Đáp án đúng là: B
Giải phương trình tìm $k.$
Đáp án cần chọn là: B
Vào năm nào thì số hươu ở khu bảo tồn gấp đôi so với năm 2021?
Đáp án đúng là: C
Đáp án cần chọn là: C
Trong khu bảo tồn, ngoài loài hươu còn có loài hổ Bengal sinh sống, theo thống kê ở thời điểm 31 tháng 12 năm 2016 số lượng hổ Bengal là 440 con. Biết số lượng hổ Bengal giảm $6\%$ mỗi năm. Vào năm nào sau đây tại khu bảo tồn thì số hươu sẽ gấp 4 số hổ Bengal?
Đáp án đúng là: C
Viết hàm biểu diễn số lượng hổ, giải phương trình tìm t thoả mãn điều kiện.
Đáp án cần chọn là: C
Phần 2: Văn học - Ngôn Ngữ
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Căn cứ vào nghĩa của từ.
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: A
Căn cứ vào nghĩa của từ.
Đáp án cần chọn là: A
Chọn một từ mà cấu tạo từ của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: D
Căn cứ vào kiến thức về cấu tạo từ (từ ghép, từ láy toàn phần, từ láy bộ phận).
Đáp án cần chọn là: D
Chọn một từ mà từ loại của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: C
Căn cứ vào kiến thức về từ loại (danh từ, động từ, tính từ).
Đáp án cần chọn là: C
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án đúng là: D
Căn cứ vào nghĩa của từ.
Đáp án cần chọn là: D
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Vẫn biết “ngày mai bắt đầu từ hôm nay”, quê rồi sẽ còn nhiều _______, chỉ mong mỗi người vẫn giữ trong lòng mình một chốn đi về để mà nhớ mà thương, để đi xa muốn trở về, hạnh phúc muốn trở về, _______ càng muốn trở về.
Đáp án đúng là: B
Căn cứ hiểu biết về nghĩa của từ, ngữ cảnh.
Đáp án cần chọn là: B
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Hóa ra khi mình _______, tầm nhìn bị thu hẹp về con số 0, thì tâm trí sẽ mở ra với những cảm nhận và _______ đến vô tận.
Đáp án đúng là: A
Căn cứ vào ngữ pháp, ngữ nghĩa, từ loại, logic, phong cách.
Đáp án cần chọn là: A
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Con đường làng hằng ngày tôi đi học, đi chăn bò hay _______ theo má đi chợ huyện giờ chỉ còn trong _______.
Đáp án đúng là: D
Căn cứ vào nghĩa của từ và ngữ cảnh trong câu
Đáp án cần chọn là: D
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Nhưng không ai trong số đó dạy mình cách lắng nghe, cách _________ mọi tạp âm để nghe những thứ âm thanh mình muốn nghe nhất, từ sâu bên trong mình và cả bên trong _________.
Đáp án đúng là: B
Căn cứ vào nội dung câu văn, nghĩa của từ.
Đáp án cần chọn là: B
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây.
Dải Ngân Hà, bao gồm Trái Đất, Mặt Trời và nhiều _____ khác, liên tục di chuyển với _____ nhanh, nhưng con người lại thấy chúng bất động.
Đáp án đúng là: A
Căn cứ vào hiểu biết về nghĩa của từ, suy luận logic.
Đáp án cần chọn là: A
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Anh ấy ra sức luyện tập, nhưng kết quả đạt được vẫn không được như mong đợi.
Đáp án đúng là: C
Căn cứ vào ngữ pháp, ngữ nghĩa, logic.
Đáp án cần chọn là: C
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Bảng kế hoạch tổng rất quan trọng trong việc xác định, tổ chức thực hiện và theo dõi tiến trình thi công theo kế hoạch đã lập và theo thực tế công trường.
Đáp án đúng là: B
Căn cứ vào nghĩa của từ, ngữ cảnh.
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Tất cả các em học sinh trong kì thi giữa học kì vừa qua đã làm bài thi với thái độ nghiêm túc, nhưng kết quả không thể thuyết phục.
Đáp án đúng là: C
Căn cứ vào lỗi sai về ngữ nghĩa.
Đáp án cần chọn là: C
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Trong tương lai gần, những sản phẩm thân thiện với môi trường sẽ được tiêu thụ rộng rãi và giúp cho việc phát triển nền kinh tế của đất nước.
Đáp án đúng là: B
Căn cứ vào ngữ pháp, ngữ nghĩa, logic, phong cách
Đáp án cần chọn là: B
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Với sự quyết tâm và sáng tạo, nhóm nghiên cứu đã hoàn thành xuất sắc nhiệm vụ đã giao, tạo ra một sản phẩm mang lại giá trị thiết thực cho cộng đồng.
Đáp án đúng là: B
Căn cứ vào lỗi sai về ngữ nghĩa.
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 66 đến 70:
Ngày xưa cũng như ngày nay, thuyết tương đối âm dương vẫn gắn bó mật thiết và sâu sắc với văn hóa phương Đông, trong đó có Việt Nam. Nó được biểu hiện cụ thể, chân phương từ nhiều góc độ trong đời sống. Thứ nhất, âm dương là bản chất của giới tự nhiên. Trong đời sống, dân tộc nào cũng va chạm với các cặp đối lập “đực – cái”, “nóng – lạnh”, “cao – thấp”…Với người nông dân, họ chú trọng sự sinh sôi, nảy nở của hoa màu và con người với hai cặp đối lập Mẹ - Cha và Đất – Trời. Như vậy, Đất được đồng nhất với Mẹ, còn trời được đồng nhất với Cha. Việc hợp nhất của hai cặp “Mẹ - Cha” và “Đất – Trời”chính là sự khái quát đầu tiên trên con đường dẫn tới triết lý âm dương. Đây là yếu tố nền tảng góp phần thiết lập nên các cặp đối lập mới trong giới tự nhiên. Từ cặp “Lạnh – Nóng” có thể suy ra: Về thời tiết thì mùa đông lạnh thuộc âm, mùa hè nóng thuộc dương. Về phương hướng, phương Bắc lạnh thuộc âm, phương Nam nóng thuộc dương. Về thời gian, ban đêm lạnh thuộc âm, ban ngày nóng thuộc dương. Hay là, đêm thì tối nên màu đêm thuộc âm, ngày thì đỏ nên màu đỏ thuộc dương. Cái hay, cái đẹp của triết lý âm dương nằm ở quy luật thành tố: Không có gì hoàn toàn âm hoặc hoàn toàn dương, trong âm có dương, trong dương có âm. Nó còn được phản ánh qua quy luật quan hệ: Âm dương luôn gắn bó mật thiết và chuyển hóa cho nhau. Hai quy luật này góp phần không nhỏ vào việc đánh giá, nhìn nhận và khám phá giới tự nhiên từ góc độ bản chất. Thứ hai, những biểu hiện âm dương trong xã hội xưa và nay: Về mặt tư duy, dân gian vẫn nhận thức theo kiểu: “Chim sa, cá nhảy chớ mừng; nhện sa, xà đón xin đừng có lo”. Đây là cách diễn đạt quy luật “trong âm có dương” và “trong âm có dương”. Ngày xưa, ông cha ta còn hình thành lối tư duy theo quan hệ nhân quả, chẳng hạn: “Sướng lắm khổ nhiều” hay “Trèo cao ngã đau”. Đây là cách diễn đạt kín đáo của quy luật “Âm dương chuyển hóa”. Ngày nay, lối tư duy âm dương này được người Việt vận dụng và kết hợp khéo léo trong đời sống văn hóa. Điều này được phản ánh qua triết lý sống quân bình: Coi trọng, đề cao sự hài hòa âm dương trong cơ thể và sự hài hòa trong giới tự nhiên. Đặc trưng quân bình các yếu tố đời sống tạo ra khả năng thích nghi cao trước mọi biến cố, hoàn cảnh của dân tộc Việt từ ngàn đời. Về mặt đời sống, triết lý âm dương được biểu hiện khá rõ từ ba nhu cầu cơ bản nhất: Ăn, mặc và ở. Với nhu cầu ăn, người Việt nhấn mạnh tính cộng đồng, tính mực thước truyền thống. Trong đó, tính cộng đồng được phản ánh từ việc ăn tổng hợp, ăn chung; còn tính mực thước là biểu hiện của khuynh hướng quân bình âm dương. Nó đòi hỏi người ăn không ăn quá nhanh hay quá chậm, không ăn quá nhiều hay quá ít, không ăn hết hay ăn còn. Đây được xem là lối giao tiếp tế nhị, ý tứ khác hẳn tính cách cực đoan, lối giao tiếp trực khởi của người phương Tây: Khách phải ăn kỳ sạch để tỏ lòng biết ơn chủ nhà. Tính cộng đồng và tính mực thước trong bữa ăn thể hiện tập trung qua nồi cơm và chén nước mắm. Nồi cơm ở đầu mâm và chén nước mắm ở giữa mâm là biểu tượng cho cái đơn giản mà thiết yếu: Cơm gạo là tinh hoa của đất, mắm chiết từ cá là tinh hoa của nước – chúng giống như hành Thủy và hành Thổ là cái khởi đầu và cái trung tâm trong Ngũ Hành.
(Phan Thị Anh Thư, Triết lí âm dương trong đời sống văn hoá Việt, Theo Võ Quê)
Trả lời cho các câu 66, 67, 68, 69, 70 dưới đây:
Xác định nội dung chính của đoạn trích trên.
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Ý nghĩa của việc đồng nhất cặp Mẹ - Cha với Đất - Trời là gì?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Câu thành ngữ nào phản ánh quan niệm “âm dương chuyển hoá” theo nội dung đoạn trích trên?
Đáp án đúng là: A
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: A
Từ “quân bình” trong cụm từ “Đặc trưng quân bình” KHÔNG đồng nghĩa với từ nào dưới đây?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản, nghĩa của từ.
Đáp án cần chọn là: D
Dự đoán nội dung đoạn tiếp theo sau đoạn trích?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 71 đến 75:
Nhiễm trùng là tình trạng sức khỏe rất phổ biến, có thể ảnh hưởng đến bệnh nhân ở mọi lứa tuổi. Nhiễm trùng là tình trạng tấn công và sự tăng sinh của các vi khuẩn, virus hoặc ký sinh trùng (gọi chung là vi sinh vật)... đối với cơ thể, dẫn tới các phản ứng tế bào, tổ chức hoặc phản ứng toàn thân. Thông thường, biểu hiện trên lâm sàng là một hội chứng nhiễm khuẩn, nhiễm độc. Nhiễm trùng có thể tại một vị trí cố định hoặc đi theo đường máu lan khắp cơ thể. Vi khuẩn và virus đều là những vi sinh vật gây bệnh mà mắt thường không nhận biết được. Tuy đường lây nhiễm giữa vi khuẩn và virus khá tương tự nhau và thường lây lan theo những đường giống nhau. Triệu chứng bệnh nhiều khi cũng rất khó phân biệt, nhưng do khác biệt về cấu tạo của hai loại vi sinh này nên cách điều trị của hai loại nhiễm trùng này hoàn toàn khác nhau. Vi khuẩn là một thể duy nhất, nhưng chúng là tế bào rất phức tạp và có thể tự tồn tại bên trong hoặc bên ngoài cơ thể. Hầu hết các vi khuẩn không có hại. Trong thực tế, có nhiều vi khuẩn thường trú trên da và trong cơ thể của chúng ta, đặc biệt là trong ruột giúp tiêu hóa thức ăn. Một số vi khuẩn tự nhiên sống trong cơ thể không được coi là nhiễm trùng, ví dụ như vi khuẩn thường trú trong miệng và ruột. Virus nhỏ hơn và có cấu tạo không phải là tế bào. Không giống như vi khuẩn, chúng cần một vật chủ như con người hay động vật để nhân lên. Virus gây nhiễm trùng bằng cách nhập vào nhân bên trong các tế bào khỏe mạnh của vật chủ. Nhiễm vi khuẩn và nhiễm virus có nhiều điểm chung. Chúng cũng có thể lây lan bằng cách tương tự nhau. Các yếu tố nguy cơ gây nhiễm trùng có thể kể đến như: Tiếp xúc giọt bắn của người bệnh khi ho và hắt hơi; Tiếp xúc với người bị nhiễm, đặc biệt là thông qua hôn và quan hệ tình dục; Tiếp xúc với các bề mặt, thực phẩm và nước bị ô nhiễm; Vi khuẩn hoặc virus có thể được truyền thông qua bằng cách chạm hoặc bắt tay với một người khác. Chạm tay vào thực phẩm bẩn cũng khiến virus hoặc vi khuẩn lây lan. Chấn thương cơ thể gây các vết xây xước da. Dịch cơ thể như máu, nước bọt và tinh dịch, có thể chứa các vi khuẩn, virus gây bệnh và truyền bệnh và lây lan qua con đường dùng chung bơm kim tiêm hoặc quan hệ tình dục. Trường hợp nhiễm virus phổ biến và nặng nhất là viêm gan B và nhiễm HIV/AIDS. Tiếp xúc với sinh vật bị nhiễm bệnh qua vật chủ trung gian, bao gồm cả vật nuôi và các loài côn trùng như bọ chét và ve.
(BS. Trần Trung, Nhiễm trùng là bệnh gì?, Theo Báo Sức khoẻ và Đời sống, ngày 17/08/2020)
Trả lời cho các câu 71, 72, 73, 74, 75 dưới đây:
Nhiễm trùng được định nghĩa là gì?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Điểm khác biệt chính giữa vi khuẩn và virus là gì?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Yếu tố nguy cơ nào sau đây KHÔNG được nhắc đến trong ngữ liệu như một nguyên nhân gây nhiễm trùng?
Đáp án đúng là: B
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: B
Từ nội dung ngữ liệu, điều gì có thể được suy ra về ảnh hưởng của vi khuẩn trong cơ thể con người?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Theo ngữ liệu, vì sao việc hiểu rõ về nhiễm trùng và cách lây lan của nó lại quan trọng đối với sức khỏe cộng đồng?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Đọc đoạn trích sau và trả lời câu hỏi:
Các chính phủ - cả chuyên chế lẫn cộng hòa - đều trục xuất ông, bọn tư sản - cả bảo thủ lẫn dân chủ cực đoan - đều thi nhau vu khống và nguyền rủa ông. Mác đã gạt sang một bên tất cả những thứ đó, coi như cái mạng nhện vướng chân, chẳng thèm đếm xỉa, và chỉ đáp lại khi thấy hết sức cần thiết mà thôi.
Và ông đã mất đi, hàng triệu người cộng sự cách mạng với ông ở khắp châu Âu và châu Mĩ, từ những hầm mỏ Xi-bia đến tận Ca-li-phoóc-ni-a, đã tôn kính, yêu mến và khóc thương ông, và tôi có thể mạnh dạn nói rằng ông có thể có nhiều kẻ đối địch, nhưng chưa chắc đã có một kẻ thù nào riêng cả.
(Theo C. MÁC VÀ PH. ĂNG-GHEN, Toàn tập, tập 19, NXB Chính trị Quốc gia, Hà Nội, 1995)
Nội dung chính của đoạn trích trên là gì?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Đọc đoạn trích sau và trả lời câu hỏi:
Bác Dương thôi đã thôi rồi,
Nước mây man mác ngậm ngùi lòng ta.
Nhớ từ thuở đăng khoa ngày trước
Vẫn sớm hôm tôi bác cùng nhau;
Kính yêu từ trước đến sau,
Trong khi gặp gỡ khác đâu duyên trời?
Cũng có lúc chơi nơi dặm khách,
Tiếng suối nghe róc rách lưng đèo;
Có khi từng gác cheo leo,
Thú vui con hát lựa chiều cầm xoang.
Cũng có lúc rượu ngon cùng nhắp,
Chén quỳnh tương ăm ắp bầu xuân.
Có khi bàn soạn câu văn,
Biết bao đông bích, điển phần trước sau
(Nguyễn Khuyến, trích Khóc Dương Khuê, in trong Thơ văn Nguyễn Khuyến, NXB Văn học, Hà Nội, 1971)
Đâu không phải là kỉ niệm giữa hai người bạn được nhắc đến trong đoạn thơ?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Đọc đoạn trích sau và trả lời câu hỏi:
Nghe những lời giận dữ đó của Ra-ma, Xi-ta đau đớn đến nghẹt thở, như một cây dây leo bị vòi voi quật nát. Nghe những lời tố cáo trước đông đủ mọi người, Xi-ta xấu hổ cho số kiếp của nàng. Nàng muốn chôn vùi cả hình hài thân xác của mình. Mỗi lời nói của Ra-ma xuyên vào trái tim nàng như một mũi tên. Nước mắt nàng đổ ra như suối. Lấy tà áo lau nước mắt, rồi bằng giọng nghẹn ngào, nức nở, nàng nói: “Cớ sao chàng lại dùng những lời gay gắt khó tả như vậy đối với thiếp, giống như một kẻ thấp hèn chửi mắng một con mụ thấp hèn? Thiếp đâu phải là người như chàng tưởng! Thiếp có thể lấy tư cách của thiếp ra mà thề, hãy tin vào danh dự của thiếp. Suy từ hành vi của loại phụ nữ thấp hèn, chàng đã ngờ vực tất cả phụ nữ, nhưng như thế đâu có phải. Nếu chàng hiểu thiếp chút đỉnh, xin hãy bỏ mỗi ngờ vực không căn cứ đó đi…”.
(Van-mi-ki, Ra-ma buộc tội, theo bản dịch ra văn xuôi của Phạm Thủy Ba, NXB Văn học, Hà Nội, 1989)
Nghệ thuật tiêu biểu nhất trong đoạn trích trên là gì?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Đọc đoạn trích sau và trả lời câu hỏi:
Con phà như nhịp cầu phao
Đón những chiếc xe từ mặt trận
Những chiếc xe bụi lấm
Chở đầy hàng
Vỏ đạn pháo ánh vàng
Mũ sắt giặc bẹp dí
Cánh máy bay đạn xé...
Theo con phà sang sông
Một phía chiến trường
In lên đó
Ở buồng lái có chú sóc nhỏ
Làm xiếc trong lồng
Một dò phong lan
Lá tết đuôi sam con gái
Cũng in lên đó
Một phía chiến trường.
10-1973
(Hoàng Vũ Thuật, Một phía chiến trường, in trong Những bông hoa trên cát, NXB Bình Trị Thiên - Hội Văn học nghệ thuật Bình Trị Thiên, 1979)
Hình ảnh trung tâm của bài thơ trên là gì?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Đọc đoạn trích sau và trả lời câu hỏi:
Khi nhìn cách tôi cầm sách trong giờ tập đọc, hiển nhiên cô đã nhận thấy có gì không bình thường; cô liền thu xếp cho tôi đi khám mắt... Thật ra, tôi ngạc nhiên về hành động đó đến nỗi không nhận biết được chuyện gì đã xảy ra, cho tới một ngày kia cô đưa cho tôi một cặp kính.
“Em không thể nhận được. Em không có tiền trả đâu”, tôi nói, cảm thấy xấu hổ vì nhà mình nghèo. Cô liền kể chuyện cho tôi nghe: “Hồi cô còn nhỏ, một người hàng xóm đã mua kính cho cô. Bà ấy bảo một ngày kia cô sẽ trả cặp kính đó bằng cách tặng kính cho một cô bé khác. Em thấy chưa, cặp kính này đã được trả tiền từ trước khi em ra đời.” Thế rồi cô nói với tôi những lời nồng hậu nhất mà chưa ai từng nói với tôi: “Một ngày nào đó em sẽ mua kính cho một người khác”. Cô làm tôi thành người có trách nhiệm. Cô tin tôi có thể có một cái gì để trao cho người khác.
(Theo Bin-li Đa-vít, trong “Trái tim người thầy”, NXB Trẻ, TP. Hồ Chí Minh, 2004)
Thông điệp chính của đoạn văn trên là gì?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Đọc đoạn trích sau và trả lời câu hỏi:
Bóng thuyền thấp thoáng dờn trên vách
Làn sóng long bong vỗ trước nhà.
(Nguyễn Khuyến, Trích Nước lụt Hà Nam, Văn đàn bảo giám, Trần Trung Viên, NXB Văn học)
“Long bong” trong đoạn thơ trên thuộc kiểu từ nào?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Đọc đoạn trích sau và trả lời câu hỏi:
Về cơ bản, tính cách của chúng ta là một bộ phận của thói quen. Ngạn ngữ có câu: “Gieo suy nghĩ, gặt hành động, gieo hành động, gặt thói quen, gieo thói quen, gặt tính cách gieo tính cách, gặt số phận”. Có thể nói, thói quen là khuôn mẫu nhất quán, đôi khi Vô thức, thể hiện tính cách của chúng ta một cách thường xuyên, hàng ngày và quyết định tính hiệu quả hay không hiệu quả trong mọi hoạt động, tạo nên sức mạnh bên trong của chúng ta. Horace Mann, một nhà sư phạm vĩ đại từng nói: “Thói quen cũng giống như dây thừng. Hàng ngày chúng ta bên từng sợi nhỏ và bện càng nhiều thì sợi dây thừng càng khó đứt”. Bản thân tôi không đồng ý với phần cuối của câu nói này. Tôi cho rằng nó có thể bị đứt, cũng như thói quen là thứ có thể học và cũng có thể từ bỏ, nhưng việc đó đòi hỏi phải có một quá trình và một quyết tâm cao.
(Stephen R.Covey, Trích Bảy thói quen để thành đạt, NXB Trẻ, 2014).
Thao tác lập luận chủ yếu được tác giả sử dụng trong đoạn trích trên là gì?
Đáp án đúng là: A
Căn cứ vào kiến thức về thao tác lập luận.
Đáp án cần chọn là: A
Đọc đoạn trích sau và trả lời câu hỏi:
Phải nói ngay rằng, trong nghệ thuật, không phải cái mới nào cũng hay, nhưng chắc chắn, cái hay nào cũng mới. Tìm đến cái mới là khát vọng của bất cứ nhà thơ nào. Nói đúng hơn, nó vừa là một khát vọng, nhưng cũng là ách nặng đặt lên vai người nghệ sĩ trong hành trình sáng tạo không mệt mỏi của họ. Bởi lẽ, ngay cả những cây bút tài năng nhất, không phải bài thơ nào của họ cũng mới. Càng không phải bài thơ nào của họ cũng hay. Mỗi một thời đại thơ ca, biết làm thế nào được, số người làm thơ rất đông nhưng số thi sĩ trụ được với thời gian lại rất ít. Cũ thì đương nhiên bị loại bỏ. Còn mới? Không phải cái mới nào cũng được chấp nhận. Có những cái mới bị đào thải và có những cái mới sống mãi với thời gian. Hóa ra, việc làm mới thơ ca không hề đơn giản. Có những cái mới cốt làm hoa mắt độc giả, nhưng sau khi đọc xong bài thơ, thậm chí, phải cần đến một thời gian sau, người ta mới nhận ra đó là cái mới giả. Còn có những cái mới thoạt đầu, rất ít người thừa nhận, nhưng dần theo thời gian, càng ngày người ta càng nhận thấy những lớp hào quang ẩn chứa bên trong. Đó là cái mới thật.”
(Nguyễn Đăng Điệp, Trích Thơ Việt Nam hiện đại tiến trình và hiện tượng, tham luận ở Văn Miếu Quốc Tử Giám, nhân Ngày Thơ lần thứ II, 5/2/2004)
Đoạn trích trên sử dụng kiểu cấu trúc đoạn văn nào?
Đáp án đúng là: C
Căn cứ vào kiến thức về kiểu cấu trúc đoạn văn.
Đáp án cần chọn là: C
Đọc đoạn trích sau và trả lời câu hỏi:
Tương tư thức mấy đêm rồi,
Biết cho ai, hỏi ai người biết cho!
Bao giờ bến mới gặp đò?
Hoa khuê các bướm giang hồ gặp nhau?
(Nguyễn Bính, Tương tư, in trong Tuyển tập Nguyễn Bính, NXB Văn học, Hà Nội, 1986)
Đoạn thơ trên đã tái hiện cảm xúc nào của nhân vật trữ tình?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Đọc đoạn trích sau và trả lời câu hỏi:
Thời gian như gió thoảng qua
Tình yêu là cánh đồng hoa giữa trời
Tay ta nắm lấy tay người
Dẫu qua trăm suối ngàn đồi cũng qua
(Xuân Quỳnh, Hát ru II, in trong Tự hát, NXB Tác phẩm mới, 1984)
Trong câu thơ thứ hai, tác giả muốn khẳng định điều gì?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 86 đến 90:
Dựa trên thí nghiệm của Michelson và Morley, nhà vật lý người Ailen, George Fitzgerald và nhà vật lý người Hà Lan, Hendrik Lorentz đã gợi ý rằng các vật thể chuyển động trong ête sẽ co lại và đồng hồ sẽ chạy chậm đi. Sự co lại này cũng như sự chậm lại của đồng hồ chính là điều làm cho chúng ta đo được ánh sáng với cùng tốc độ, không phụ thuộc vào việc chúng chuyển động như thế nào so với ête (Fitzgerald và Lorentz vẫn còn coi ête là một vật chất có thật). Tuy nhiên, trong bài báo viết năm 1905, Einstein đã chỉ ra rằng nếu không thể nhận biết được sự chuyển động so với ête thì khái niệm về ête là hoàn toàn không cần thiết. Thay vào đó, ông đề xuất tiên đề cho rằng các định luật khoa học phải là như nhau đối với mọi người quan sát chuyển động tự do, cụ thể là họ phải đo được tốc độ ánh sáng như nhau, không phụ thuộc vào việc họ chuyển động như thế nào. Tốc độ ánh sáng không phụ thuộc vào chuyển động của họ và như nhau theo mọi hướng.
Tiên đề này đòi hỏi phải từ bỏ ý tưởng cho rằng có tồn tại một đại lượng phổ biến gọi là thời gian mà mọi đồng hồ đều đo được như nhau. Thay vào đó, mỗi người quan sát sẽ có thời gian riêng của mình. Thời gian của hai người sẽ giống nhau nếu họ đứng yên so với nhau nhưng sẽ chênh lệch nếu họ chuyển động tương đối với nhau.
(Stephen Hawking, Vũ trụ trong vỏ hạt dẻ, NXB Trẻ, TP. HCM, 2022, tr10-13)
Trả lời cho các câu 86, 87, 88, 89, 90 dưới đây:
Thí nghiệm của Michelson và Morley đã chứng minh điều gì về sự chuyển động của ánh sáng?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Fitzgerald và Lorentz cho rằng sự co lại của vật thể trong ête có tác dụng gì đối với tốc độ ánh sáng?
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Theo Einstein, khi hai người quan sát chuyển động với nhau, thời gian của họ sẽ như thế nào?
Đáp án đúng là: C
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: C
Quan điểm của Einstein về thời gian có ảnh hưởng gì đến cách chúng ta hiểu về “thời gian tuyệt đối”?
Đáp án đúng là: A
Căn cứ vào nội dung phần cuối của văn bản.
Đáp án cần chọn là: A
Einstein đề xuất tiên đề rằng các định lý khoa học phải giống nhau đối với mọi người quan sát chuyển động tự do. Điều này có ý nghĩa gì trong việc bác bỏ khái niệm ête?
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Đọc đoạn trích dưới đây và trả lời các câu hỏi từ 91 đến 95:
Tôi biết nơi kia có một chỗ ngồi
Một phiến đá bên hồ xanh thẳm
Thuở ưu tư tôi thường ngồi ngắm
Bóng chim trời lặng lẽ bay qua
Con chim nào giấu mặt trong sương
Khi chiều xuống cùng tôi trò chuyện
Chim hỏi tôi: Người từ đâu đến?
Thưa chim rằng: Tôi từ cỏ sinh ra
Tôi trở về tìm trong hương cỏ
Dịu dàng một chút bình yên
Tự do nhiều khi là im lặng
Để đừng nghe ai gọi tên
Tôi biết nơi kia có một chỗ ngồi
Tháng năm qua tôi không trở lại
Lẽ thường thôi dù muôn vàn cát bụi
Người phải đi hết cuộc hành trình
Tháng năm tôi đi tới chân trời
Thở bát ngát giữa đời lộng gió
Khi chân mỏi bên đường nắng nỏ
Dưới cây kia tôi ngồi hát nghêu ngao
Tôi biết nơi kia có một chỗ ngồi
Đã lâu lắm tôi chưa trở lại
Chắc bây giờ, chim trời - cỏ dại...
(Hoàng Phủ Ngọc Tường, Tôi biết nơi kia có một chỗ ngồi, Tạp chí Sông Hương)
Trả lời cho các câu 91, 92, 93, 94, 95 dưới đây:
Hình ảnh “con chim” trong bài thơ có thể được hiểu theo ý nghĩa nào?
Chọn đáp án đúng nhất.
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Điền vào chỗ trống để có nhận định phù hợp nhất với nội dung bài thơ:
“Chỗ ngồi” trong bài thơ không chỉ là một địa điểm vật lý mà còn là _______, nơi con người tìm về để suy ngẫm về cuộc đời và những gì đã qua.
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Hình ảnh “con chim” trong bài thơ có thể liên hệ với ý nghĩa nào dưới đây trong văn học?
Đáp án đúng là: A
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: A
Sắp xếp các ý sau theo đúng trình tự diễn biến tâm trạng của nhân vật trữ tình trong bài thơ:
(1)Tìm về "chỗ ngồi" để chiêm nghiệm cuộc sống.
(2) Nhận thức rằng cuộc đời là hành trình không thể dừng lại.
(3) Cảm nhận sự hòa hợp với thiên nhiên, tìm kiếm bình yên.
(4) Đi xa, đối diện với cuộc sống rộng lớn nhưng cũng đầy thử thách.
Đáp án đúng là: D
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: D
Nhận định nào dưới đây thể hiện đúng tư tưởng chính của bài thơ?
Chọn đáp án đúng nhất
Đáp án đúng là: B
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: B
Đọc đoạn trích dưới đây và trả lời các câu hỏi:
Hỏi mẹ Khờ có từng quay lại không, người núi Xanh nói biết đâu, giờ nhiều du khách lên đây, mặt mũi ai cũng dáo dác như ai, nhớ sao nổi người phụ nữ mấy chục năm về trước. Thằng nhỏ hay bị du khách ghẹo, họ xưng mẹ nè con, mau về với mẹ. “Mẹ tui nói chừng đá trổ bông mới lên đón, giờ có trổ xíu nào đâu”, Khờ nói. Chỉ một lời dối ầu ơ, nhưng với bộ não ngờ nghệch của Khờ, đã thành một thứ dây trói bền dai, buộc nó mãi trên đỉnh núi. Mẹ Khờ có ở đây, chắc gì lay chuyển được nó, đá chưa nở bông nào.
Dân núi Xanh có lần hối tiếc, khi xúm nhau thuyết phục Khờ, rằng đám đá đó đâu thể trổ bông được, sét đánh quá chừng mà, nhìn thì biết, tới cỏ còn không mọc nổi. Khờ nói luôn, vậy mấy cục đá hong bị trời đánh thể nào cũng có bông. Từ bữa đó nó leo trèo khắp núi. Lo bông đá đang trổ ở hang hốc nào đó, nơi nó chưa mò tới. Còn cả xóm thì phấp phỏng sợ nó trượt chân.
Mình mà nói núi này đá đực khó ra bông, Khờ sẽ hỏi, vậy núi nào mới có? Tôi hình dung vậy, khi ngó thằng nhỏ vừa gánh xong đôi nước cuối cùng trong ngày, đổ vào cái khạp da bò đặt ngay đỉnh trọc. Nước ấy dành cho du khách uống đỡ khát. Dù họ chỉ dùng rửa mặt, rửa chân, hắt vào người nhau cho vui.
Nắng vẫn xéo xắt, chưa chịu nguội. Tôi quay lại đúng cái chân núi mà vài tiếng đồng hồ trước mình đứng ngán ngẩm vì nắng và hồ Xanh cạn đáy. Nghĩ chắc cũng không cần trèo lên chi, quá biết trên đó có những thứ gì, lại miễu cậu miễu cô, lại những quán xá đu theo vách đá, lại bày bán mấy thứ thần dược từ cỏ cây meo mốc chớ đâu.
Nhưng Khờ xuất hiện, với đôi thùng nước treo đầu gánh, rủ khơi khơi, lên núi chơi, bông đá nay mai sẽ trổ.
(Nguyễn Ngọc Tư, Đá trổ bông, In trong Biển người mênh mông, NXB Trẻ, TP. Hồ Chí Minh, 2012)
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Nhân vật Khờ trong đoạn trích hiện lên với đặc điểm nào?
Đáp án đúng là: A
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: A
Phương thức trần thuật nào được sử dụng trong đoạn văn?
Đáp án đúng là: A
Căn cứ vào nội dung đoạn trích, kiến thức về phương thức trần thuật.
Đáp án cần chọn là: A
Hình ảnh “bông đá” trong đoạn văn mang ý nghĩa biểu tượng nào?
Đáp án đúng là: B
Căn cứ vào nội dung của văn bản.
Đáp án cần chọn là: B
Vì sao người dân núi Xanh lại “có lần hối tiếc” khi thuyết phục Khờ rằng đá không thể trổ bông?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C
Chi tiết nào sau đây KHÔNG thể hiện sự đối lập giữa niềm tin của Khờ và thực tế?
Đáp án đúng là: C
Căn cứ vào nội dung văn bản.
Đáp án cần chọn là: C