Phần 1: Tư duy Toán học
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km ) đã lái xe mỗi ngày trong một tháng ở bảng sau:

| Đúng | Sai | |
|---|---|---|
| a) Khoảng tứ phân vị của mẫu số liệu ghép nhóm gần bằng 79,17 . | ||
| b) Khoảng biến thiên của mẫu số liệu ghép nhóm là \(250(\mathrm{~km})\). | ||
| c) Số trung bình của mẫu số liệu ghép nhóm là 145. |
Đáp án đúng là: Đ; Đ; S
áp dụng công thức tính số trung bình, phương sai, tứ phân vị
Đáp án cần chọn là: Đ; Đ; S
Kéo thả vào chỗ thích hợp
Cho a,b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của hàm số \(y = {\log _a}x,{\mkern 1mu} {\mkern 1mu} y = {\log _b}x,{\mkern 1mu} {\mkern 1mu} y = {\log _c}x\).
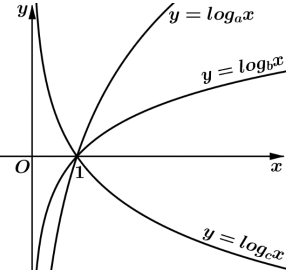
Khi đó<<
Đáp án đúng là: c; b; a
Dựa vào tính đồng biến nghịch biến
Đáp án cần chọn là: c; b; a
Một hình lăng trụ có tổng của số lượng đỉnh, số lượng cạnh và số lượng mặt bằng 32. Hình lăng trụ đó có số cạnh bằng:
Đáp án đúng là: C
Hình lăng trụ \(n\) giác có \(2n\) đỉnh, \(3n\) cạnh và \(n + 2\) mặt.
Đáp án cần chọn là: C
Kéo thả vào ô trống:
Cho các dãy số $\left( u_{n} \right)$ gồm $u_{n} = \sqrt{n^{2} + 1}$, $u_{n} = n + \dfrac{1}{n}$, $u_{n} = 2^{n} + 1$, $u_{n} = \dfrac{n}{n + 1}$. Khi đó
- Có dãy số bị chặn
- Có dãy số tăng
Đáp án đúng là: 1; 4
Dãy số bị chặn khi nó bị chặn dưới và chặn trên
Dãy số tăng khi có $u_{n + 1} > u_{n}\forall n$
Đáp án cần chọn là: 1; 4
Cho hàm số \(y = f(x) = {x^2} - \dfrac{2}{x} + 1\) có đồ thị \((C)\). Tiếp tuyến của \((C)\) tại điểm có hoành độ \(x = 2\) có hệ số góc bằng?
Đáp án đúng là: D
Tiếp tuyến của \((C)\) tại điểm có hoành độ \(x = 2\) có hệ số góc là y’(2)
Đáp án cần chọn là: D
Trong không gian với hệ toạ độ Oxyz, cho điểm $M\left( {1;0;1} \right)$ và hai mặt phẳng $(Q):x + y - 3z - 5 = 0$, $(R):x + 2y - z - 1 = 0$. Xét tính đúng sai của các khẳng định sau:
| Đúng | Sai | |
|---|---|---|
| a) Khoảng cách từ điểm $M$ đến mặt phẳng $(Q)$ bằng $\dfrac{7}{\sqrt{11}}$. | ||
| b) Mặt phẳng đi qua $M$ và song song với mặt phẳng $(Q)$ có phương trình là: $x + y - 3z - 2 = 0$ | ||
| c) Mặt phẳng đi qua điểm $A\left( {1; - 2;0} \right)$ và vuông góc với hai mặt phẳng $(Q):x + y - 3z - 5 = 0$, $(R):x + 2y - z - 1 = 0$ có phương trình là $5x - 2y + z - 9 = 0$. |
Đáp án đúng là: Đ; Đ
a) áp dụng công thức tính khoảng cách
b) tìm VTPT $\overset{\rightarrow}{n}\ = \left\lbrack {\overset{\rightarrow}{n_{1}};\overset{\rightarrow}{n_{2}}} \right\rbrack$
Đáp án cần chọn là: Đ; Đ
Trong các hàm số sau$y = \dfrac{\tan 2x}{\tan^{2}x + 1}$, $y = \sin x\cos 2x$, $y = \cos x\sin^{2}x$, $y = \cos x\sin^{3}x$ có hàm số chẵn
Đáp án đúng là: 1
Hàm chẵn: $\forall x \in D,{\mkern 1mu} {\mkern 1mu} f\left( { - x} \right) = f\left( x \right)$.
Hàm lẻ: $\forall x \in D,{\mkern 1mu} {\mkern 1mu} f\left( { - x} \right) = {\mathrm{ \;}} - f\left( x \right)$.
Đáp án cần chọn là: 1
Trong tập số nguyên có các số “đặc biệt” mà tổng và tích bởi hai số tự nhiên khác bằng nhau ví dụ như $4 = 2 + 2 = 2.2$. Hỏi có bao nhiêu số là các số “đặc biệt”
Đáp án đúng là: 2
Gọi số tổng quát mà thỏa mãn $xy = x + y$
Đáp án cần điền là: 2
Biết tồn tại số nguyên dương \(x,y\) và số nguyên tố \(p\) thỏa mãn\({p^x} - {y^4} = 4\). Khi đó giá trị của \(p\) bằng
Đáp án đúng là: 5
Phân tích \({y^4} + 4\) thành nhân tử rồi sử dụng tính chất của số nguyên tố.
Đáp án cần điền là: 5
Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò chơi dân gian đánh đu. Trong trò chơi này, khi người chơi nhún đều thì cây đu sẽ đưa người chơi dao động qua lại ở vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy rằng khoảng cách \(h\) (tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \(t\,\,(t \ge 0\) và được tính bằng giây) bởi hệ thức \(h = \left| d \right|\) với\(d = 3\cos \left[ {\dfrac{\pi }{3}\left( {2t - 1} \right)} \right]\). Trong đó quy ước rằng \(d > 0\) khi vị trí cân bằng ở phía sau lưng người chơi đu và \(d < 0\) trong trường hợp trái lại. Tìm thời điểm đầu tiên sau 10 giây mà người chơi đu ở xa vị trí cân bằng nhất.
Đáp án đúng là: D
Vị trí xa cân bằng nhất là ở biên nên cho \({h_{\max }}\), tìm \(t\) nhỏ nhất thỏa mãn.
Đáp án cần chọn là: D
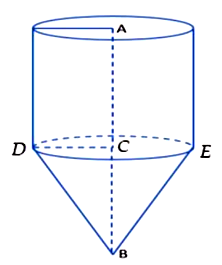
Người ta thiết kế một cái phễu có dạng gồm một hình trụ và một hình nón như hình vẽ.
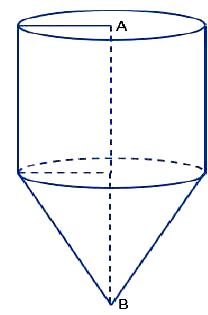
Biết chiều cao của phễu là \(AB = 6{\rm{\;cm}}\). Phần hình nón có thiết diện qua trục là một tam giác đều và thể tích phần khối trụ bằng 6 lần thể tích khối nón. Tính thể tích cái phễu đó, làm tròn kết quả tới hàng phần trăm.
Đáp án đúng là: B
Đáp án cần chọn là: B
Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \(A\left( {800;500;7} \right)\) đến điểm \(B\left( {940;550;9} \right)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là \(C(x;y;z)\). Tính \(x + y + z\).
Đáp án đúng là: 1595
Đáp án cần điền là: 1595
Tìm hệ số của \({x^8}\) trong khai triển của biểu thức \({\left( {\dfrac{4}{x} - {x^3}} \right)^8}\).
Đáp án đúng là: B
Sử dụng khai triển nhị thức Niu-tơn: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}} \).
Đáp án cần chọn là: B
Biết \(\int\limits_0^1 {\dfrac{{2{x^2} + 3x + 3}}{{{x^2} + 2x + 1}}\;{\rm{d}}x} = a - \ln b\) với a, b là các số nguyên dương. Tính \(P = {a^2} + {b^2}\).
Đáp án đúng là: 13
Đáp án cần điền là: 13
Cho hàm số $f(x) = \dfrac{ax - 6}{bx - c}(a,b,c \in {\mathbb{R}})$ có bảng biến thiên như sau:
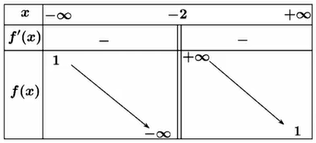
Xét tính đúng sai của các khẳng định sau
| Đúng | Sai | |
|---|---|---|
| a) Hàm số có tất cả 2 đường tiệm cận | ||
| b) Hệ số $a > 0$ | ||
| c) Trong 3 số a, b, c có 2 số âm |
Đáp án đúng là: Đ; S; Đ
Dựa vào đường tiệm cận, tính nghịch biến để xác định dấu của các hệ số
Đáp án cần chọn là: Đ; S; Đ
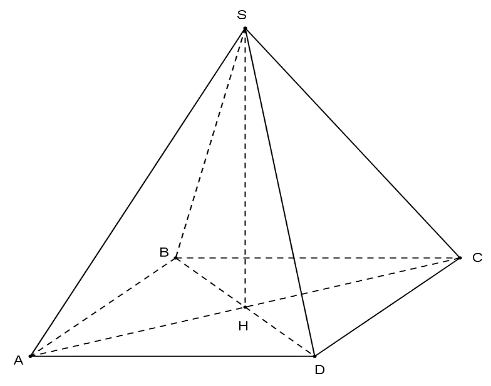
Cho khối chóp tứ giác đều có cạnh đáy bằng \(a\), cạnh bên gấp hai lần cạnh đáy. Tính thể tích \(V\) của khối chóp đã cho:
Đáp án đúng là: A
Thể tích khối chóp chiều cao \(h\), diện tích đáy \(B\) là: \(V = \dfrac{1}{3}Bh\).
Đáp án cần chọn là: A
Biết rằng đồ thị \((H):y = \dfrac{{{x^2} + 2x + m}}{{x - 2}}\) (với \(m\) là tham số thực) có hai điểm cực trị là A, B. Hãy tính khoảng cách từ gốc tọa độ \(O(0;0)\) đến đường thẳng AB.
Đáp án đúng là: A
Đáp án cần chọn là: A
Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc \(110^\circ \) và có độ lớn lần lượt là \(9N,\,\,4N\), lực \(\overrightarrow {{F_3}} \) vuông góc với mặt bàn và có độ lớn \(7N\). Độ lớn hợp lực của ba lực trên là \(a\left( N \right)\), tìm giá trị của \(a\) (kết quả quy tròn về số nguyên)
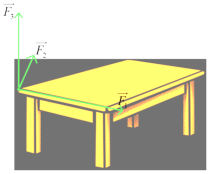
Đáp án đúng là: 11
Đáp án cần điền là: 11
Cho \({\rm{lo}}{{\rm{g}}_2}3 = a,{\rm{lo}}{{\rm{g}}_2}5 = b\). Khi đó \({\rm{lo}}{{\rm{g}}_{15}}8\) bằng
Đáp án đúng là: C
Đáp án cần chọn là: C
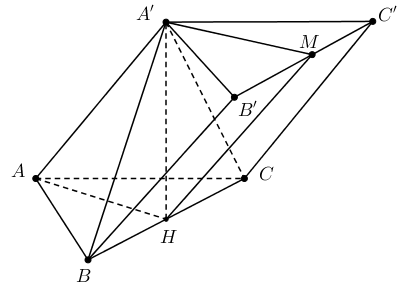
Cho khối lăng trụ \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(A'A = A'B = A'C = a\). Biết góc giữa hai mặt phẳng \(\left( {BCC'B'} \right)\) và \(\left( {ABC} \right)\) bằng \({30^ \circ }\), thể tích của khối lăng trụ đã cho bằng
Đáp án đúng là: C
Gọi H là trung điểm BC, M là trung điểm của B’C’
\( \Rightarrow A'H \bot \left( {ABC} \right)\) và \(A'MH = {30^0}\) từ đó tìm BC, AH và tính thể tích lăng trụ.
Đáp án cần chọn là: C
Từ các chữ số trong tập hợp \(X = \left\{ {0;1;2;3;4;5;6} \right\}\) thì có thể lập được bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhu có dạng \(\overline {abcdef} \) sao cho \(a + b = c + d = e + f\)
Đáp án đúng là: A
Xét các trường hợp:
TH1: \(a + b = c + d = e + f = 7\)
TH2: \(a + b = c + d = e + f = 6\)
TH3: \(a + b = c + d = e + f = 5\)
Đáp án cần chọn là: A
Xét tính đúng sai của khẳng định sau
| Đúng | Sai | |
|---|---|---|
| a) $7^{89} - 4^{81}$ có chữ số tận cùng là 3 | ||
| b) $2^{2014} \cdot 9^{1955}$ có chữ số tận cùng là 6 |
Đáp án đúng là: Đ; Đ
Đưa lũy thừa về các số đặc biệt để được số có tận cùng là 1, 5, 6
Đáp án cần chọn là: Đ; Đ
Khẳng định nào sau đây là đúng?
Đáp án đúng là: C
Tính chất đường thẳng vuông góc với mặt phẳng
Đáp án cần chọn là: C
Trên giá sách có 4 quyển sách Toán, 3 quyển sách Lý, 2 quyển sách Hóa. Lấy ngẫu nhiên 3 quyển sách. Xác suất để 3 quyển lấy ra có ít nhất 1 quyển là môn Toán có dạng $\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính hiệu b - a?
Đáp án đúng là: 5
Tính số cách lấy không có quyển Toán
Đáp án cần điền là: 5
Trong không gian với hệ trục tọa độ \(Oxyz\) cho tam giác \(ABC\) với \(A\left( {4;0;2} \right)\); \(B\left( {1; - 4; - 2} \right)\) và \(C\left( {2;1;1} \right).\). Khi đó
Diện tích của tam giác \(ABC\) bằng
Tọa độ điểm \(D (m,n,p\) thỏa mãn \(\;ABCD\) là hình bình hành thì \(m+n-p=\)
Gọi điểm \(E\left( {a;b;c} \right)\) là giao điểm của đường thẳng \(BC\) với mặt phẳng tọa độ \(\left( {Oxz} \right)\) khi đó \(\dfrac{{2a}}{c} + b =\)
Đáp án đúng là: \(\dfrac{\sqrt{210}}{2}\); 5; 9
Đáp án cần chọn là: \(\dfrac{\sqrt{210}}{2}\); 5; 9
Trong hệ tọa độ Oxyz cho hai mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 2}}{3} + \dfrac{{y - 1}}{2} + \dfrac{{z - 4}}{{ - 6}} = 1\) và \(\left( Q \right):{\mkern 1mu} x + 2y + 3z + 7 = 0\). Tính tang góc tạo bởi hai mặt phẳng đã cho.
Đáp án đúng là: D
Cho \(\left( \alpha \right):{a_1}x + {b_1}y + {c_1}z + {d_1} = 0,\,\,\,\left( \beta \right):{a_2}x + {b_2}y + {c_2}z + {d_2} = 0\) nhận \(\overrightarrow {{n_1}} = ({a_1};{b_1};{c_1}),\,\,\overrightarrow {{n_2}} = ({a_2};{b_2};{c_2})\) lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) được tính:
Đáp án cần chọn là: D
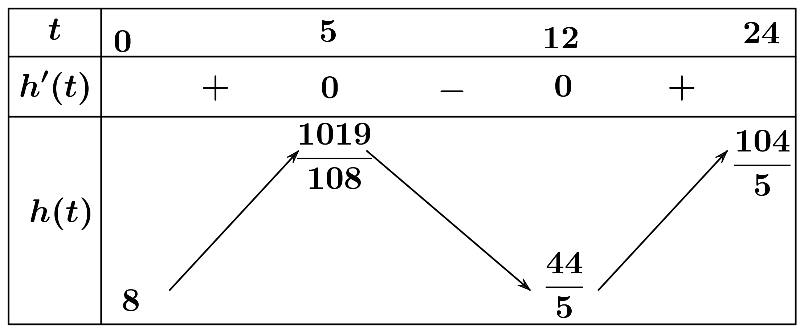
Mực nước trong hồ chứa của nhà máy điện thủy triều thay đổi trong suốt một ngày do nước chảy ra khi thủy triều xuống và nước chảy vào khi thủy triều lên (như hình vẽ). Tốc độ thay đổi của mực nước được xác định bởi hàm số \(h'(t) = \dfrac{1}{{90}}\left( {{t^2} - 17t + 60} \right)\), trong đó \(t\) tính bằng giờ \(\left( {0 \le t \le 24} \right)\), \(h'(t)\) tính bằng mét/giờ. Tại thời điểm \(t = 0\), mực nước trong hồ chứa cao \(8m\). Mực nước trong hồ cao nhất bằng m và thấp nhất bằng m.
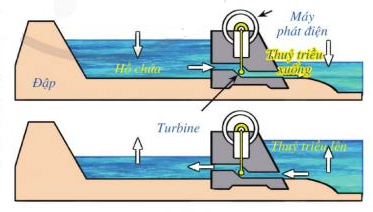
Đáp án đúng là: 20,8; 8
Tìm nguyên hàm của h'(x) để xác định hàm độ cao h(x) từ đó tìm GTLN, GTNN
Đáp án cần chọn là: 20,8; 8
Một cốc hình trụ có đường kính đáy bằng 7cm, chiều cao 15cm . Trong cốc chứa một lượng nước bằng \(\dfrac{2}{3}\) thể tích cốc. Một con quạ muốn uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 3cm. Con quạ thông minh đã mổ những viên sỏi hình cầu có bán kính \(0,9\;{\rm{cm}}\) thả vào cốc để mực nước đâng lên. Hỏi để uống được nước, con quạ cần thả ít nhất bao nhiêu viên sỏi?
Đáp án đúng là: 26
Đáp án cần điền là: 26
Cho $P\left( A \middle| B \right) = \dfrac{1}{4},\, P\left( B \middle| A \right) = \dfrac{1}{3},\, P\left( {\overline{A}\overline{B}} \right) = \dfrac{1}{10}$. Khi đó, giá trị của $P(A)$ bằng:
Đáp án đúng là: B
Vận dụng công thức xác suất toàn phần, công thức xác suất có điều kiện.
Đáp án cần chọn là: B
Cho hàm số \(y=\dfrac{x^2-m x+2 m}{x+m}\) có đồ thị \(\left(C_m\right)\). Có tất cả bao nhiêu đồ thị \(\left(C_m\right)\) đi qua điểm \((0 ; 1)\).
Đáp án đúng là: C
Đáp án cần chọn là: C
Trong mặt phẳng có vectơ $\overset{\rightarrow}{v}$. Phép biến hình biến mỗi đểm $M$ thành điểm $M'$ sao cho $\overset{\rightarrow}{MM^{\prime}} = \overset{\rightarrow}{v}$ được gọi là phép tịnh tiến theo vectơ $\overset{\rightarrow}{v}$. Phép tịnh tiến theo vectơ $\overset{\rightarrow}{v}$ thường được kí hiệu là $T_{\overset{\rightarrow}{v}},$ trong đó $\overset{\rightarrow}{v}$ được gọi là vectơ tịnh tiến. Giả sử có điểm $A\left( {1,2} \right)$ và $\overset{\rightarrow}{v}\left( {2, - 1} \right)$. Khi đó $T_{\overset{\rightarrow}{v}}$ biến điểm A thành $B\left( {a,b} \right)$ thì $a.b$ bằng bao nhiêu?
Đáp án đúng là: 3
Từ định nghĩa phép tịnh tiến xác định tọa độ B
Đáp án cần điền là: 3
Cho \(G\) lậ tập giác đều và \(M\) là tập hợp 11 điểm gồm 10 đỉnh cùng với tâm của \(G\) (Hình vẽ bên). Chọn ngẫu nhiên 3 điểm thuộc \(M\), xác suất để 3 điểm được chọn lập thành một tam giác bằng
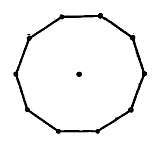
Đáp án đúng là: C
Chọn 3 điểm bất kì không thẳng hàng ta sẽ thu được một tam giác
Đáp án cần chọn là: C
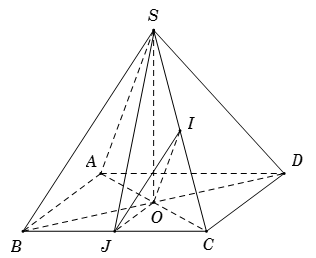
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Chọn các khẳng định đúng
Đáp án đúng là: A; C
- Cách xác định góc giữa hai mặt phẳng bằng cách đưa về góc giữa hai đường thẳng
- Xác định đường thẳng $d$//CD. Khi đó $\angle\left( {IJ,CD} \right) = \angle\left( {IJ,d} \right)$
- Thể tích hình chóp bằng $V = \dfrac{1}{3}h.S$
Đáp án cần chọn là: A; C
Cho hình vuông OABC cạnh bằng 8 , điểm M nằm trong hình vuông sao cho khoảng cách từ M đến các cạnh OA, OC cùng bằng 3. Parabol $\left( P_{1} \right)$ đi qua các điểm O, A, M, Parabol $\left( P_{2} \right)$ đi qua các điểm O, C, M. Tính diện tích phần tô đậm (hình vẽ bên). (kết quả làm tròn kết quả đến hàng đơn vị).
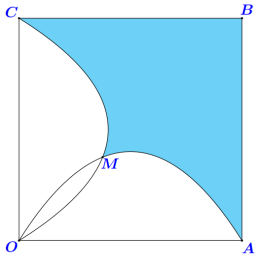
Đáp án đúng là: 32
Chọn hệ trục tọa độ Oxy sao cho tia Ox trùng tia OA, tia Oy trùng tia OC.
Chia hình thành các phần diện tích, ứng dụng tích phân để tính diện tích từng phần.
Đáp án cần điền là: 32
Tập xác định của hàm số $f(x) = \log_{2}\left( {20 - x^{2}} \right)$ chứa bao nhiêu số nguyên?
Đáp án đúng là: 9
Hàm số $y = \log_{2}\left( {f(x)} \right)$ xác định khi $f(x) > 0$
Đáp án cần điền là: 9
Tổng các nghiệm của phương trình \(\cos 3x - \sin 3x = \sqrt 2 \) với \(x \in \left( { - \dfrac{\pi }{2};\pi } \right)\) có dạng \(a.\pi\). Khi đó giá trị của \(2a\) bằng
Đáp án đúng là: 1
Biến đổi \(\cos 3x - \sin 3x\) về dạng \(\sin \left( {\dfrac{\pi }{4} - 3x} \right)\)
Đáp án cần điền là: 1
Số nghiệm nguyên của bất phương trình $\left( {x - 10} \right)\left( {4 - 5^{x}} \right) > 0$ bằng
Đáp án đúng là: 9
Dựa vào tính đồng biến nghịch biến
Đáp án cần điền là: 9
Có 1 kho bia kém chất lượng chứa các thùng giống nhau (24 lon/thùng) gồm 3 loại: loại I để lẫn mỗi thùng 3 lon quá hạn sử dụng, loại II để lẫn mỗi thùng 2 lon quá hạn và loại III để lẫn mỗi thùng 4 lon quá hạn. Biết số lượng thùng loại I gấp 2 lần số lượng thùng loại II và số thùng loại II gấp 3 lần thùng loại III. Chọn ngẫu nhiên 1 thùng từ trong kho, từ đó chọn ngẫu nhiên 10 lon. Tính xác suất để lấy được 2 lon quá hạn sử dụng (làm tròn đến kết quả phần chục).
Đáp án đúng là: 0,3
Gọi \({A_i}\) là biến cố chọn được thùng loại \(i.(i = I,II,III)\)
\(B\) là biến cố chọn được 10 sản phẩm trong đó có 2 lon quá hạn từ thùng được chọn ra.
Bài toán trở thành tìm \(P\left( B \right)\) bằng công thức xác suất toàn phần.
Đáp án cần điền là: 0,3
Gọi \(M, m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\dfrac{3 \sin x+2}{\sin x+1}\) trên đoạn \(\left[0 ; \dfrac{\pi}{2}\right]\). Khi đó giá trị của \(M^2+m^2\) là
Đáp án đúng là: B
Đáp án cần chọn là: B
Trong không gian, cho hình chóp \(S \cdot ABCD\) có đáy là hình bình hành tâm \(O, M\) là điểm thay đổi trên \(S O\). Khi biểu thức \(P=M S^2+M A^2+M B^2+M C^2+M D^2\) đạt giá trị nhỏ nhất thì ti số \(\dfrac{S M}{S O}\) bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười)
Đáp án đúng là: 0,8
Đáp án cần điền là: 0,8
Phần 2: Tư duy đọc hiểu
Dữ liệu số là tài nguyên để xây dựng thành phố thông minh
Theo Bộ Thông tin và Truyền thông, hiện đã có 54 địa phương tại Việt Nam triển khai các đề án liên quan đến đô thị thông minh, tập trung vào các lĩnh vực như giao thông, môi trường, y tế và hành chính. Tuy nhiên, chỉ có khoảng 30% các dự án đạt được mức tích hợp dữ liệu liên thông giữa các ngành, lĩnh vực.
“Dữ liệu hiện đang bị phân tán, thiếu sự đồng nhất và còn hạn chế trong việc phục vụ công tác ra quyết định,” ông Hồ Đức Thắng, Phó Cục trưởng Cục Chuyển đổi số Quốc gia, Bộ Thông tin và Truyền thông, nhận định.
Thực tế cho thấy, cơ sở dữ liệu đồng bộ không chỉ hỗ trợ cải cách hành chính mà còn là nền tảng để phát triển các ứng dụng thông minh. Thượng tá Nguyễn Thành Vĩnh, Giám đốc Trung tâm Dữ liệu Quốc gia về Dân cư, chia sẻ: “Hệ thống dữ liệu dân cư quốc gia hiện đã tích hợp hơn 87,9 triệu thông tin cá nhân, tạo điều kiện cho các dịch vụ định danh điện tử và nâng cao hiệu quả dịch vụ công.” Điều này không chỉ tiết kiệm thời gian và chi phí mà còn tăng tính minh bạch trong quản lý.
Hiện nay, nhiều địa phương trên cả nước đã đạt được những kết quả nổi bật trong hành trình này. Tại Đà Nẵng, hệ thống dữ liệu liên thông đã giúp thành phố điều hành thông minh và tối ưu hóa các dịch vụ công. Các tỉnh như Bình Dương hay Quảng Ninh cũng đang triển khai mạnh mẽ các giải pháp IoT và dữ liệu lớn để nâng cao năng lực quản lý và thúc đẩy phát triển kinh tế số. Những mô hình này không chỉ mang lại giá trị riêng lẻ mà còn tạo tiền đề cho sự hợp tác và chia sẻ kinh nghiệm giữa các địa phương.
Theo Phó Giám đốc Sở Thông tin và Truyền thông TP. Đà Nẵng, ông Trần Ngọc Thạch, Trung tâm Điều hành Thông minh (IOC) đã trở thành hình mẫu về ứng dụng dữ liệu trong quản trị đô thị. Ông cho biết: “Việc tích hợp dữ liệu từ hơn 20 cơ quan không chỉ giúp điều hành hiệu quả mà còn mở ra cơ hội phát triển các ứng dụng sáng tạo từ cộng đồng.” Nhờ sự kết nối liên thông này, Đà Nẵng đã trở thành một trong những thành phố tiên phong của Việt Nam trong lĩnh vực chuyển đổi số.
Một yếu tố không thể thiếu trong bức tranh này là việc khai thác dữ liệu lớn (Big Data). TS. Cù Kim Long, chuyên gia AI và dữ liệu lớn tại Viện Công nghệ Thông tin, Đại học Quốc gia Hà Nội, cho rằng: “Dữ liệu lớn không chỉ giúp dự đoán các xu hướng như biến đổi khí hậu hay tăng trưởng dân số mà còn đóng vai trò quan trọng trong việc nâng cao khả năng cạnh tranh của các đô thị trên toàn cầu.”
Tại hội thảo, nhiều chuyên gia chỉ ra rằng, để dữ liệu thực sự trở thành “trái tim” của thành phố thông minh, việc đảm bảo an toàn thông tin là yếu tố tiên quyết. Bà Võ Thị Trung Trinh, Giám đốc Trung tâm Chuyển đổi số TP.HCM, nhận định: “Các hệ thống dữ liệu cần được xây dựng trên nền tảng bảo mật vững chắc để bảo vệ quyền riêng tư của người dân và tạo niềm tin với cộng đồng.”
Trong hành trình xây dựng đô thị thông minh, vai trò của doanh nghiệp, chính quyền và cộng đồng là không thể tách rời. Từ các tập đoàn lớn đến doanh nghiệp vừa và nhỏ, tất cả đều góp phần cung cấp giải pháp công nghệ và dịch vụ số, hỗ trợ quản trị đô thị hiệu quả hơn. Để thúc đẩy sự tham gia này, việc xây dựng một "sân chơi chung" thông qua kiến trúc chính quyền số đồng bộ và các cơ chế chính sách rõ ràng là điều kiện tiên quyết.
Tuy nhiên, một trong những thách thức lớn nhất là việc dữ liệu hiện nay vẫn còn bị phân tán và thiếu tính liên thông. Đây không chỉ là vấn đề ở cấp quốc gia mà còn xuất hiện giữa các tỉnh thành, khi các hệ thống dữ liệu chưa được đồng bộ hóa để hỗ trợ phát triển vùng. Việc thúc đẩy sử dụng các nền tảng chung và chia sẻ dữ liệu ngang hàng giữa các địa phương sẽ giúp giảm chi phí và tối ưu hóa nguồn lực, đồng thời tạo ra hiệu quả lớn hơn trong việc cung cấp dịch vụ công và quản lý đô thị.
Hành trình chuyển đổi số và phát triển đô thị thông minh không phải là câu chuyện của riêng một thành phố hay một tỉnh, mà là trách nhiệm chung của tất cả các địa phương. Sự hợp lực giữa các tỉnh thành, từ Bắc vào Nam, sẽ là chìa khóa để Việt Nam xây dựng một mạng lưới đô thị thông minh bền vững và hiện đại.
(Hoàng Nam, Cơ sở dữ liệu là chìa khóa xây dựng Thành phố thông minh, kinhtedothi.vn, 2/12/2024)
Trả lời cho các câu 41, 42, 43, 44, 45, 46, 47, 48, 49, 50 dưới đây:
Việc chỉ khoảng 30% dự án đô thị thông minh đạt được mức tích hợp dữ liệu liên thông phản ánh điều gì về tư duy triển khai chuyển đổi số hiện nay tại các địa phương?
Đáp án đúng là: B
Đọc hiểu nội dung toàn bài.
Đáp án cần chọn là: B
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Theo Thượng tá Nguyễn Thành Vĩnh, hệ thống dữ liệu dân cư quốc gia đã giúp tiết kiệm chi phí và nâng cao minh bạch trong quản lý.
Đúng hay sai?
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A
Điền từ còn thiếu vào chỗ trống:
Việc thiếu sự liên thông và đồng nhất trong chia sẻ dữ liệu giữa các địa phương khiến cho việc ra quyết định và quản lý đô thị trở nên __________ và thiếu hiệu quả.
Đáp án đúng là: rời rạc
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần điền là: rời rạc
Theo quan điểm của ông Hồ Đức Thắng, đâu là nguyên nhân gốc rễ khiến dữ liệu tại các địa phương chưa hỗ trợ tốt cho việc ra quyết định?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Hoàn thành đoạn văn sau bằng cách kéo thả từ đúng vào mỗi vị trí:
Việc khai thác không chỉ giúp xu hướng phát triển như biến đổi khí hậu hay tăng dân số mà còn hỗ trợ xây dựng hệ thống quản trị thông minh có tính và hiệu quả cao. Tuy nhiên, để làm được điều đó, cần đảm bảo giữa các hệ thống và nền tảng .
Đáp án đúng là: dữ liệu lớn; dự đoán; bảo mật; liên thông; đồng bộ
Xét logic câu từ và thông tin có được sau bài đọc.
Đáp án cần chọn là: dữ liệu lớn; dự đoán; bảo mật; liên thông; đồng bộ
Vì sao Trung tâm Điều hành Thông minh (IOC) của Đà Nẵng được xem là hình mẫu điển hình?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B
Từ quan điểm của các chuyên gia trong bài, hãy xác định: điều kiện bắt buộc để dữ liệu trở thành “trái tim” của đô thị thông minh là gì?
Đáp án đúng là: C
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần chọn là: C
Từ thông tin trong văn bản, có thể rút ra thông điệp tổng quát nào về vai trò của dữ liệu trong xây dựng đô thị thông minh?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Chọn 2 đáp án đúng: Vai trò của doanh nghiệp và cộng đồng trong quá trình chuyển đổi số là:
Đáp án đúng là: A; D
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A; D
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Trong hành trình xây dựng đô thị thông minh, dữ liệu không chỉ là yếu tố kỹ thuật mà còn đóng vai trò như một công cụ __________, giúp liên kết chính quyền, doanh nghiệp và cộng đồng trong cùng một hệ sinh thái số.
Đáp án đúng là: kết nối
Xét logic câu từ.
Đáp án cần điền là: kết nối
ÔNG NGOẠI
(Nguyễn Ngọc Tư, Nhà xuất bản trẻ 2001.)
“Lược phần đầu: Người nhà Dung đi nước ngoài, Dung sang ở với ông ngoại. Ban đầu Dung không hòa nhập được với cuộc sống mới, than thở với mẹ và người mẹ khuyên cố gắng chăm ông thay mẹ…
Dung anh ách lái xe về nhà ngoại, cậu đi để lại chiếc Chaly màu xanh, Dung dùng đi học. Hồi sáng này, ông ngoại dắt xe ra đến cửa Dung hỏi:
– Ngoại định đi đâu
– Ông lên quận một chút.
Dung ngăn:
– Thôi, ngoại già rồi, không nên lái xe, có đi, con chở ông đi.
Ông tỏ vẻ giận, quầy quả vào nhà. Ôi, người già sao mà khổ đến vậy.
Thế nghĩa là có hai thế giới ở trong ngôi nhà. Thế giới của ông là mấy ông bạn già, là mấy chồng nhựt báo, là cái radio đâu hồi còn đánh nhau, là trầm tư suy ngẫm, là mảnh sân hoa trái. Thế giới của Dung là tiếng nhạc gào thét xập sinh, là sắc màu xanh đỏ, là quả đất như nằm gọn trong bàn tay. Sáng nó dậy thật sớm để nấu cơm, sau đó đi học, chiều lại học, buổi tối nó vù xe đến bạn chơi hoặc về nhà nghe mấy đứa em cãi nhau ỏm tỏi. Hai thế giới vừa giành giựt vừa hoà tan nhau.
Mặc dầu Dung đang ở trong thế giới của ông, mà không biết mình đang chìm dần vào đấy…
Có những sự thay đổi Dung không thể ngờ được. Bây giờ mỗi đêm Dung trở mình nghe ông ngoại ho khúc khắc. Nghe cây mai nhỏ nứt mình, nảy chồi Dung nghiện hương trầm tối tối ông thắp lên bàn thờ bà ngoại. Lắm khi lũ em Dung sang, chúng nó phá phách quậy tung cả lên, Dung mắng, chúng nó trề môi “Chị hai khó như một bà già”, Dung giật mình. Có lẽ quen với cái tĩnh lặng trong sân mà mỗi chiều Dung giúp ông tưới cây, cái khoảng không xanh lạc lõng trong khói bụi, đâu đó, trên tàng me già, dăm chú chim hót líu lo Dung quen dáng ông ngoại với mái tóc bạc, với đôi mắt hõm, cái cằm vuông, quen mỗi tháng một lần cọc cạch lên phường lương hưu. Có một điều Dung ngày càng nhận ra tiếng ho của ông ngày càng khô và rời rạc như lời kêu cứu. Chủ nhật Dung cắm cúi lau chùi bên dàn karaoke phủ bụi, ông đứng lên nheo mắt:
– Sao con không hát, con hát rất hay mà.- Dung thoáng ngỡ ngàng, nó hỏi:
– Ngoại có thích nghe không?
Rồi mở máy. Hôm ấy Dung rất vui, lần đầu tiên nó hát cho riêng ông nghe và quan trọng nhất là ông đã ngồi lại đấy, gật gù.
…
Hết mùa me dốt, ông cháu Dung nhặt là mai đón Tết. Cậu gửi thư và quà về. Ông ôm chầm lấy thư bảo Dung.
– Con đọc ngoại nghe.
Dung đọc một lèo, lúc ngước lên đã thấy mắt ông đỏ rưng. Ông đến bàn thờ bà, đốt nén hương, mùi trầm ngào ngạt, Dung hỏi:
– Ngoại thương cậu như vậy, sao không theo cậu?
Ông trìu mến:
– Ngoại muốn mỗi năm cùng con đón giao thừa và nghe con hát”.
( Ông ngoại, Nguyễn Ngọc Tư, Nhà xuất bản trẻ 2001.)
*Chú thích: Nguyễn Ngọc Tư: sinh năm 1976, quê ở Cà Mau, là nữ nhà văn trẻ của Hội nhà văn Việt Nam. Nguyễn Ngọc Tư thường viết về những điều bình dị, gần gũi xung quanh cuộc sống của mình. Giọng văn chị đậm chất Nam Bộ, là giọng kể mềm mại mà thâm trầm, sâu cay về những cuộc đời éo le, những số phận chìm nổi. Cái chất miền quê sông nước ngấm vào các tác phẩm, thấm đẫm cái tình của làng, của đất, của những con người chân chất hồn hậu nhưng ít nhiều gặp những bất hạnh. Truyện ngắn “Ông ngoại” với một cốt truyện đơn giản nhưng chủ đề, đề tài có giá trị nhân văn cao, khiến người đọc phải suy ngẫm về nhiều điều có giá trị của cuộc sống.
Trả lời cho các câu 51, 52, 53, 54, 55, 56, 57, 58, 59, 60 dưới đây:
Dựa vào thông tin dưới đây để trả lời các câu sau
Anh Thành vay của ngân hàng 400 triệu đồng để làm kinh tế với lãi suất là 1%/ tháng.
Trả lời cho các câu 51, 52, 53 dưới đây:
Nếu sau đúng 3 năm kể từ ngày vay, anh Thành trả toàn bộ gốc lẫn lãi cho ngân hàng thì số tiền anh Thành phải trả gần nhất với số nào dưới đây?
Đáp án đúng là: B
Áp dụng công thức: $T = A.\left( {1 + r} \right)^{n}$.
Đáp án cần chọn là: B
Biết sau đúng 1 tháng kể từ ngày vay, anh Thành bắt đầu trả nợ cho ngân hàng. Hai lần trả nợ liên tiếp cách nhau đúng 1 tháng, mỗi lần trả nợ, anh Thành trả cho ngân hàng số tiền là như nhau. Sau đúng 4 năm kể từ ngày vay ngân hàng, anh Thành đã trả hết nợ. Số tiền hằng tháng anh Thành phải trả cho ngân hàng gần nhất với số nào sau đây?
Đáp án đúng là: A
Vay ngân hàng số tiền là A đồng với lãi suất $r$/ kì hạn. Sau đúng một kì hạn kể từ ngày vay, bắt đầu hoàn nợ. Hai lần hoàn nợ cách nhau đúng một kì hạn, mỗi lần hoàn nợ số tiền là X đồng. Số tiền nợ còn lại sau khi đã trả được n kì hạn là:
$S_{n} = A.\left( {1 + r} \right)^{n} - X.\dfrac{\left( {1 + r} \right)^{n} - 1}{r}$.
Đáp án cần chọn là: A
Biết sau đúng 1 tháng kể từ ngày vay, anh Thành bắt đầu trả nợ cho ngân hàng. Hai lần trả nợ liên tiếp cách nhau đúng 1 tháng, mỗi lần anh Thành trả cho ngân hàng 10 triệu đồng. Sau 12 lần trả nợ ngân hàng, do công việc kinh doanh tiến triển thuận lợi, anh Thành quyết định trả cho ngân hàng 100 triệu đồng rồi đến đúng 1 tháng sau, anh bắt đầu trả cho ngân hàng 5 triệu đồng mỗi tháng. Hỏi cần ít nhất bao nhiêu tháng kể từ ngày vay ngân hàng, anh Thành trả hết nợ?
Đáp án đúng là: C
Vay ngân hàng số tiền là A đồng với lãi suất $r$/ kì hạn. Sau đúng một kì hạn kể từ ngày vay, bắt đầu hoàn nợ. Hai lần hoàn nợ cách nhau đúng một kì hạn, mỗi lần hoàn nợ số tiền là X đồng. Số tiền nợ còn lại sau khi đã trả được n kì hạn là:
$S_{n} = A.\left( {1 + r} \right)^{n} - X.\dfrac{\left( {1 + r} \right)^{n} - 1}{r}$.
Đáp án cần chọn là: C
Tác giả đã thể hiện hai thế giới “ông – cháu” trong ngôi nhà bằng thủ pháp nghệ thuật nào?
Đáp án đúng là: B
Liên hệ với kiến thức về ngôi kể, đối chiếu với đặc điểm của bài đọc.
Đáp án cần chọn là: B
Sự “giật mình” của Dung khi bị em trêu “khó như bà già” phản ánh điều gì?
Đáp án đúng là: A
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A
Hình ảnh “tiếng ho của ông ngày càng khô và rời rạc như lời kêu cứu” mang ý nghĩa gì?
Đáp án đúng là: C
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần chọn là: C
Thông điệp lớn nhất mà truyện ngắn gửi đến người đọc là gì?
Đáp án đúng là: C
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: C
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Ông ngoại trong truyện không chỉ là người già yếu cần chăm sóc, mà còn là người giàu tình cảm, âm thầm giữ gìn những __________ gia đình.
Đáp án đúng là: giá trị
Đọc hiểu nội dung toàn bài, kết hợp với ngữ cảnh câu văn.
Đáp án cần điền là: giá trị
Không gian sân vườn, cây mai, mùi trầm… trong truyện có thể xem như biểu tượng cho điều gì?
Đáp án đúng là: C
Đọc hiểu nội dung toàn bài, nắm được bút pháp nghệ thuật mà tác giả sử dụng chủ yếu.
Đáp án cần chọn là: C
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Việc ông ngoại từ chối theo cậu ra nước ngoài cho thấy ông sợ xa quê, không quen môi trường mới.
Đúng hay sai?
Đáp án đúng là: B
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: B
Hoàn thành đoạn văn sau bằng cách kéo thả từ đúng vào mỗi vị trí:
Ông ngoại gật gù nghe Dung hát:
Dung mắng các em khi chúng phá phách:
Dung lặng lẽ giúp ông tưới cây:
Đáp án đúng là: ghi nhận; trưởng thành; quan tâm
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Đáp án cần chọn là: ghi nhận; trưởng thành; quan tâm
Từ truyện ngắn “Ông ngoại”, em rút ra được điều gì trong mối quan hệ giữa người trẻ và người cao tuổi trong xã hội hiện đại? (Chọn 2 ý đúng)
Đáp án đúng là: A; D
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Đáp án cần chọn là: A; D
Phần 3: Tư duy khoa học/Giải quyết vấn đề
Hình 1 mô tả một động cơ phản lực:
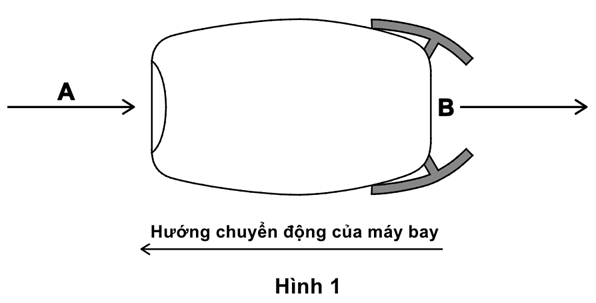
Không khí đi vào động cơ tại A bằng một chiếc quạt hút không khí. Sau đó, không khí được giữ lại bên trong động cơ, tại đó một máy nén tạo áp suất cho không khí. Nhiên liệu được đưa vào, một tia lửa được đốt cháy, khiến hỗn hợp nhiên liệu và không khí cháy. Không khí bị đốt cháy nhanh chóng nở ra và được dẫn qua một vòi phun, được đặt ở phía sau động cơ. Khí được làm nóng thoát ra khỏi B với tốc độ lớn hơn, tạo ra lực đẩy cho máy bay.
Trả lời cho các câu 61, 62, 63, 64, 65, 66, 67 dưới đây:
Phát biểu sau đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) Động lượng của không khí đi qua động cơ không đổi. |
Đáp án đúng là: S
Sử dụng dữ kiện từ đề bài: “Khí được làm nóng thoát ra khỏi B với tốc độ lớn hơn”
Động lượng: p = m.v
Đáp án cần chọn là: S
Điền số/từ/cụm từ thích hợp vào chỗ trống:
Để giải thích tại sao không khí tác dụng lực lên động cơ theo hướng về phía trước, sử dụng định luật Newton thứ ______.
Đáp án đúng là: 2 và 3
Sử dụng lý thuyết về chuyển động bằng phản lực
Đáp án cần điền là: 2 và 3
Trong một giây, một khối lượng không khí 210 kg đi vào A. Tốc độ của khối lượng không khí này tăng 570 m/s khi nó đi qua động cơ. Tính lực mà không khí tác dụng lên động cơ.
Đáp án đúng là: A
Xung lực: \(F = \dfrac{{\Delta p}}{{\Delta t}} = \dfrac{{m\Delta v}}{{\Delta t}}\)
Đáp án cần chọn là: A
Tính lực đẩy của động cơ phản lực nếu khí thoát ra có tốc độ 600 m/s và lưu lượng khí qua động cơ là 2 kg/s.
Đáp án đúng là: C
Động lượng: p = mv
Xung lượng của lực: \(\overrightarrow F = \dfrac{{\Delta \overrightarrow p }}{{\Delta t}}\)
Đáp án cần chọn là: C
Khi máy bay hạ cánh, động cơ phản lực của nó tác dụng lực giảm tốc lên máy bay bằng cách sử dụng các tấm chắn gió. Những tấm chắn gió này khiến không khí thoát ra khỏi động cơ bị lệch theo một góc so với hướng máy bay đang bay như trong Hình 2.
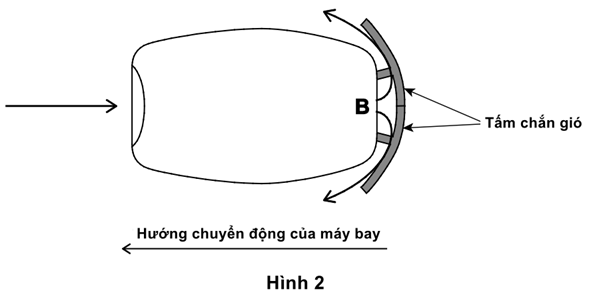
Tốc độ của không khí rời khỏi B bằng tốc độ của không khí bị lệch hướng.
Kéo thả từ/cụm từ tương ứng vào chỗ trống:
Động lượng là đại lượng . Không khí bị lệch hướng với tốc độ không đổi nên động lượng của không khí .
Đáp án đúng là: vector; thay đổi
Động lượng là đại lượng vector
Động lượng cùng hướng với vận tốc
Đáp án cần chọn là: vector; thay đổi
Giả sử tổng hợp lực giảm tốc theo phương ngang tác dụng lên các tấm chắn của động cơ phản lực có độ lớn không đổi và bằng 190 kN. Máy bay hạ cánh trên đường băng với tốc độ 68 m/s. Tính quãng đường máy bay di chuyển dọc theo đường băng cho đến khi dừng lại. Biết máy bay có khối lượng \({7.10^4}\,\,kg\).
Đáp án đúng là: D
Gia tốc: \(a = \dfrac{F}{m}\)
Mối liên hệ giữa tốc độ, quãng đường, gia tốc: \({v^2} - {v_0}^2 = 2as\)
Đáp án cần chọn là: D
Thực tế lực giảm tốc do các tấm chắn gió tạo ra có thể không giữ nguyên. Nguyên nhân nào sau đây là đúng?
Đáp án đúng là: A; B; D; E
Suy nghĩ các yếu tố thực tế có thể thay đổi tác động lên lực giảm tốc của tấm chắn gió: tốc độ của gió, tốc độ của máy bay, lượng không khí hút vào…
Đáp án cần chọn là: A; B; D; E
Phương pháp đầu dò điện trở (Electrical Resistance Probe) là phương pháp được sử dụng để đo tốc độ ăn mòn trong đường ống dẫn chất lỏng hoặc khí ăn mòn. Đầu dò được làm từ cùng loại kim loại với đường ống. Lượng kim loại bị ăn mòn được xác định thông qua sự thay đổi của giá trị điện trở đầu dò. Tốc độ ăn mòn của dây trong đầu dò giống như trong đường ống. Phương pháp này có thể được sử dụng trong hầu hết các môi trường.
Hình ảnh đầu dò được biểu diễn ở hình 1. Hình 2 là sơ đồ mạch điện đơn giản phương pháp đầu dò điện trở.
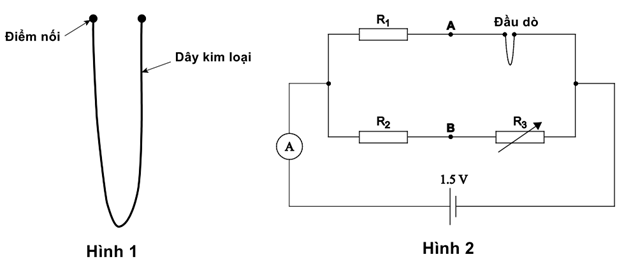
Trả lời cho các câu 68, 69, 70, 71, 72, 73, 74 dưới đây:
Dây dẫn trong một đầu dò chưa sử dụng có điện trở là \(0,07\,\,\Omega \) và chiều dài là 0,50 m. Biết điện trở suất của kim loại trong dây dẫn bằng \(9,{7.10^{ - 8}}\,\,\Omega m\). Tính đường kính của dây dẫn (Đơn vị: mm, kết quả lấy đến ba chữ số có nghĩa).
_______
Đáp án đúng là: 0,939
Điện trở dây dẫn kim loại: \(R = \rho \dfrac{l}{S}\)
Tiết diện dây dẫn: \(S = \dfrac{{\pi {d^2}}}{4}\)
Đáp án cần điền là: 0,939
Ban đầu điều chỉnh \({R_3}\) đến giá trị sao cho số chỉ của ampe kế là 0,66 A. Cho điện trở trong của nguồn không đáng kể. Trong các phát biểu dưới đây, phát biểu nào đúng, phát biểu nào sai?
| Đúng | Sai | |
|---|---|---|
| a) Tổng điện trở của mạch là \(2,3\,\,\Omega \). | ||
| b) Điện trở của \({R_1}\) là \(2,4\,\,\Omega \). Cường độ dòng điện qua đầu dò là 0,61 A. | ||
| c) Điện trở của \({R_2}\) là \(22\,\,\Omega \). Giá trị điện trở của \({R_3}\) là \(6,5\,\,\Omega \). |
Đáp án đúng là: S; S; S
Cường độ dòng điện toàn mạch: \(I = \dfrac{E}{{R + r}}\)
Hiệu điện thế: U = I.R
Điện trở tương đương của mạch điện gồm các điện trở mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\)
Điện trở tương đương của mạch điện gồm các điện trở mắc song song: \({R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Đáp án cần chọn là: S; S; S
Tính phần trăm thay đổi đường kính của đầu dò khi điện trở của nó tăng 1,6%.
Đáp án đúng là: A
Điện trở dây dẫn kim loại: \(R = \rho \dfrac{l}{S}\)
Tiết diện dây dẫn: \(S = \dfrac{{\pi {d^2}}}{4}\)
Đáp án cần chọn là: A
Điền từ/cụm từ thích hợp vào chỗ trống:
Khi đầu dò hoạt động, số chỉ của ampe kế _______.
Đáp án đúng là: giảm
Điện trở dây dẫn kim loại: \(R = \rho \dfrac{l}{S}\)
Điện trở tương đương của mạch điện gồm các điện trở mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\)
Điện trở tương đương của mạch điện gồm các điện trở mắc song song: \({R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Cường độ dòng điện toàn mạch: \(I = \dfrac{E}{{R + r}}\)
Hiệu điện thế: U = I.R
Đáp án cần điền là: giảm
Phương pháp đầu dò có thể áp dụng cho các loại ống dẫn khác ngoài kim loại không?
Đáp án đúng là: B
Kim loại là chất dẫn điện tốt
Đáp án cần chọn là: B
Cho biết tiết diện giảm 20% mỗi năm. Sau bao lâu thì tiết diện chỉ còn một nửa giá trị ban đầu?
Đáp án đúng là: D
Thiết lập biểu thức tiết diện còn lại theo thời gian
Đáp án cần chọn là: D
Ampe kế có ĐCNN 0,01 A. Khi đầu dò bị ăn mòn hết, số chỉ ampe kế là ______ A.
Đáp án đúng là: 0,05
Khi đầu dò bị ăn mòn hết, mạch điện tại đây bị đứt, không có dòng điện chạy qua nó
Điện trở tương đương của mạch điện gồm các điện trở mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\)
Điện trở tương đương của mạch điện gồm các điện trở mắc song song: \({R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Cường độ dòng điện toàn mạch: \(I = \dfrac{E}{{R + r}}\)
Hiệu điện thế: U = I.R
Đáp án cần điền là: 0,05
ĐIỆN PHÂN DUNG DỊCH
Điện phân là quá trình oxi hóa – khử xảy ra trên bề mặt các điện cực dưới tác dụng của dòng điện một chiều đi qua trong dung dịch chất điện li hoặc chất điện li nóng chảy. Ở quá trình điện phân của các ion trong nước, các ion sẽ di chuyển về phía điện cực mang điện tích trái dấu với nó. Các ion kim loại kiềm, kiềm thổ (Na+, K+, Ca2+…) và gốc muối có chứa oxygen (NO3-, CO32-,…) không tham gia quá trình điện phân mà nước sẽ bị điện phân. Tại điện cực dương (anode), xảy ra quá trình oxi hoá với sự nhường electron của chất có tính khử mạnh hơn, trong khi đó tại điện cực âm (cathode), xảy ra quá trình khử với sự nhận electron của chất có tính oxi hoá mạnh hơn.
Ví dụ quá trình điện phân nước ở mỗi điện cực
Anode: 2H2O ⟶ O2 + 4H+ + 4e
Cathode: 2H2O + 2e ⟶ H2 + 2OH-
Một trong những ứng dụng của phương pháp điện phân là mạ điện - đó là quá trình phủ một lớp kim loại lên bề mặt kim loại khác. Trong quá trình mạ điện, vật cần mạ được gắn với điện cực âm, kim loại mạ là một thanh nguyên chất được gắn với cực dương và cùng nhúng trong dung dịch chứa ion kim loại cần mạ. Khi có dòng điện chạy qua, các ion kim loại di chuyển về cực âm, bị khử thành kim loại và phủ lên vật cần mạ. Trên thực tế, để thu được lớp mạ sáng bóng, có độ bám tốt thì còn phải chú ý nhiều yếu tố khác như pH, nhiệt độ, cũng như thành phần và nồng độ các chất trong dung dịch.
Trả lời cho các câu 75, 76, 77, 78, 79, 80 dưới đây:
Những phát biểu nào dưới đây là đúng?
Khi điện phân dung dịch NaCl có màng ngăn thì
Đáp án đúng là: A; B; C
Đọc đoạn văn và trả lời câu hỏi.
Đáp án cần chọn là: A; B; C
Điền từ/cụm từ thích hợp vào chỗ trống?
Các vật làm bằng nhôm thường khá bền do có lớp màng oxide Al2O3 khó bị ăn mòn bởi các tác nhân oxi hoá. Người ta có thể tạo ra lớp oxide đó bằng phương pháp điện phân dung dịch acid với một điện cực làm bằng vật dụng nhôm cần tạo lớp màng oxide. Khi đó nhôm sẽ phản ứng với khí oxygen sinh ra ở điện cực nhờ quá trình điện phân nước. Vật dụng bằng nhôm được nối với điện cựccủa dòng điện một chiều. Tại bề mặt nhôm xảy ra quá trình .
Đáp án đúng là: dương; oxi hóa
Nguyên tắc điện phân:
(-) Cathode: xảy ra quá trình khử
(+) Anode: xảy ra quá tình oxi hóa
Đáp án cần chọn là: dương; oxi hóa
Người ta có thể tách các cation kim loại ra khỏi dung dịch bằng cách điện phân phân đoạn (điện phân khống chế hiệu điện thế áp đặt vào hai cực), khi đó cation có tính oxi hoá lớn hơn sẽ bị điện phân trước và tách nước ra. Điện phân phân đoạn (với điện cực trơ) dung dịch chứa các ion Ag+, Cu2+, Ni2+ và Mg2+ với anion $NO_{3}^{-}$. Cation nào sẽ bị điện phân trước tại cathode?
Đáp án đúng là: D
Căn cứ vào dữ liệu đoạn văn:’’cation có tính oxi hoá lớn hơn sẽ bị điện phân trước và tách nước ra’’.
Đáp án cần chọn là: D
Nhận định dưới đây là đúng hay sai?
‘’Trong sản xuất vỏ hộp, người ta có thể tráng thiếc (Sn) lên bề mặt thép bằng phương pháp điện phân với anode làm bằng Sn và cathode là vật làm bằng thép cần được mạ’’
Đáp án đúng là: A
Nguyên tắc mạ điện:
Quá trình xảy ra trong bình điện phân:
Anode (+): xảy ra quá trình oxi hóa
Cathode (-): xảy ra quá trình khử
Đáp án cần chọn là: A
Kéo thả cụm từ thích hợp vào chỗ trống?
Trong quá trình mạ điện, khối lượng cathode, khối lượng anode.
Đáp án đúng là: tăng lên; giảm xuống
Căn cứ vào dữ liệu đoạn văn.
Đáp án cần chọn là: tăng lên; giảm xuống
Người ta muốn mạ nickel lên một vật X có có diện tích 100 cm2, độ dày của lớp nikel phủ đều trên bề mặt là a μm. Dòng điện chạy qua bình điện phân có cường độ 0,5 A và thời gian mạ là 5 giờ. Giá trị của a là bao nhiêu? (Kết quả làm tròn đến hàng phần mười). Biết nikel có khối lượng mol nguyên tử là 58,7 g/mol; hoá trị II; khối lượng riêng là 8,8.103 kg/m3 và số mol nikel bám vào bề mặt vật X được tính theo công thức n =$\dfrac{I.t}{N.F}$
Trong đó:
t là thời gian điện phân (giây).
n là số mol chất sinh ra ở điện cực (mol).
N là số electron trao đổi.
F là hằng số Faraday (F = 96500).
I là cường độ dòng điện (A).
Đáp án đúng là: 31,1
Áp dụng công thức nNi =\(\dfrac{{I.t}}{{N.F}}\)
Đáp án cần điền là: 31,1
CITRULLINE
L – citrulline là một α – amino acid không thiết yếu có thể được tổng hợp trong cơ thể từ các hợp chất khác. L – citrulline có khả năng giảm đau mỏi cơ, tăng sức bền vận động và cải thiện chức năng sinh lí nam. Loại amino acid này được bổ sung vào đồ uống sinh dưỡng thể thao và được xem là một loại thực phẩm chức năng dạng viên hay bột.
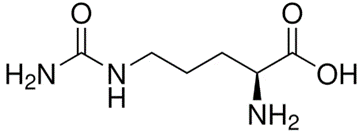
L – citrulline
Dưa hấu là một loại trái cây giàu L – citrulline. Phương pháp quang phổ hấp thụ UV-Vis được sử dụng để xác định hàm lượng L – citrulline trong vỏ trắng và thịt quả của dưa hấu dựa trên sự hình thành hợp chất màu (độ hấp thụ cực đại ở 490 nm đối với citrulline) do phản ứng của L – citrulline với diacetyl monoxime trong môi trường acid. Ánh sáng của bước sóng chiếu vào hỗn hợp phản ứng. Độ hấp thụ ánh sáng của hỗn hợp phản ứng sẽ được thiết bị đo được và giá trị này tỉ lệ thuận với nồng độ L – citrulline trong một phạm vi nhất định.
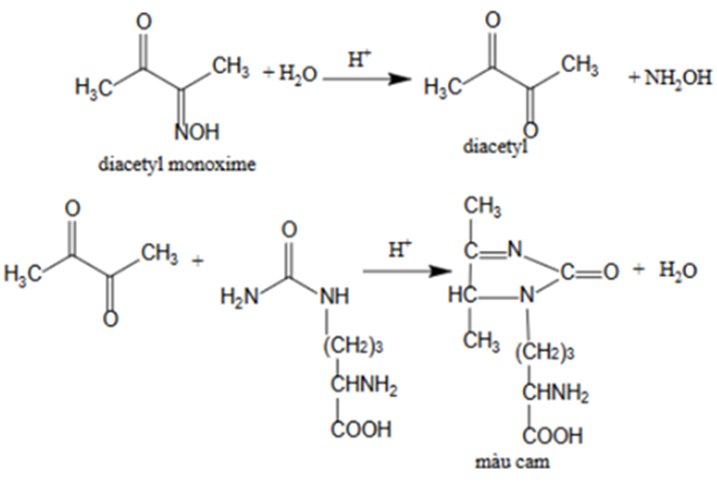
Phản ứng tạo hợp chất màu của L - citrulline với diacetyl monoxime
Tiến hành phân tích hàm lượng L – citrulline có trong vỏ trắng, thịt quả của dưa hấu ở 4 địa điểm khác nhau bằng phương pháp quang phổ hấp thụ UV-Vis từ hàm lượng L – citrulline được quy đổi theo trọng lượng khô, thu được kết quả như hình 1:
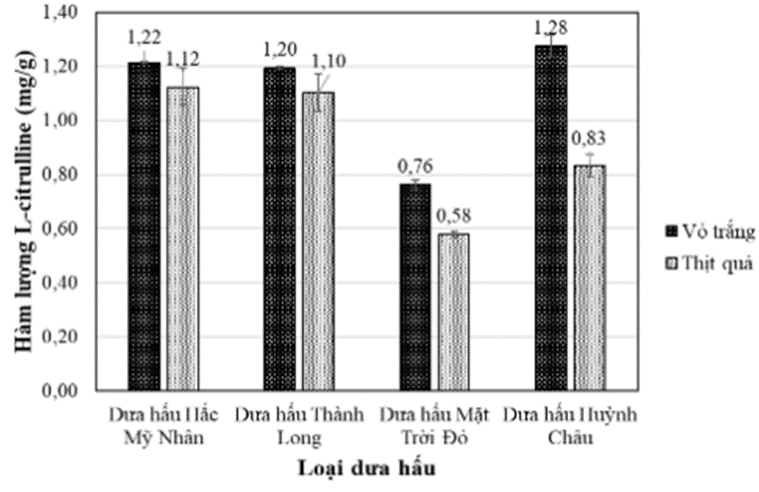
Hình 1: Hàm lượng L – Citrulline phân bố trong các loại dưa hấu khác nhau
Trả lời cho các câu 81, 82, 83, 84, 85, 86, 87 dưới đây:
Công thức phân tử của L - citrulline là
Đáp án đúng là: A
Từ CTCT để suy ra CTPT.
Đáp án cần chọn là: A
Những phát biểu nào sau đây là đúng về L – citrulline?
Đáp án đúng là: A; B; E
Từ CTCT để suy ra tính chất.
Căn cứ vào dữ liệu đoạn văn.
Đáp án cần chọn là: A; B; E
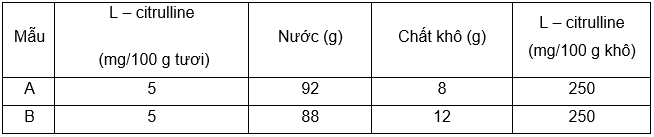
Phát biểu dưới đây là đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| a) L - citrulline phản ứng với với diacetyl monoxime được thực hiện trong môi trường acid. | ||
| b) Nồng độ L – citrulline càng lớn thì độ hấp thụ càng giảm. | ||
| c) Số nguyên tử hydrogen trong hợp chất màu cam là 17. | ||
| d) Hợp chất màu cam là hợp chất có chứa vòng. |
Đáp án đúng là: Đ; S; Đ; Đ
Căn cứ vào phản ứng tạo hợp chất màu của L - citrulline với diacetyl monoxime.
Đáp án cần chọn là: Đ; S; Đ; Đ
Hàm lượng L – citrulline có trong thịt quả ở 4 địa điểm tính theo trọng lượng khô dao động từ
Đáp án đúng là: B
Phân tích dữ liệu hình 1.
Đáp án cần chọn là: B
Kéo thả từ/cụm từ thích hợp vào chỗ trống?
’Hàm lượng L – citrulline phân bốtrong quả dưa hấu, trong đó vỏ trắng chứathịt quả của các loại dưa hấu khác nhau.’’
Đáp án đúng là: khác nhau; nhiều hơn
Phân tích dữ liệu hình 1.
Đáp án cần chọn là: khác nhau; nhiều hơn
Để sản xuất được 100 hộp thuốc có chứa L – citrulline thì cần bao nhiêu tấn vỏ trắng khô của dưa hấu Hắc Mỹ Nhân. Biết hàm lượng L – citrulline có trong 1 viên thuốc là 1200 mg. Mỗi hộp thuốc chứa 120 viên? (Làm tròn kết quả đến hàng phần mười)
Đáp án đúng là: 11,8
Phân tích dữ liệu đề bài.
Đáp án cần điền là: 11,8
Nhận định dưới đây là đúng hay sai?
‘’ Khi so sánh hàm lượng L – citrulline giữa các mẫu dưa hấu, nếu không quy đổi theo trọng lượng khô thì có thể dẫn đến kết kết quả sau lệch do ảnh hưởng của lượng nước trong mẫu’’
Đáp án đúng là: A
Phân tích căn cứ vào dữ liệu kết hợp với kiến thức thực tế.
Đáp án cần chọn là: A
Đọc đoạn thông tin sau và trả lời các câu hỏi:
NUÔI CẤY VI SINH VẬT ĐỂ THU SINH KHỐI
Vi sinh vật có kích thước rất nhỏ, có tỉ lệ diện tích bề mặt/ thể tích (S/V) rất lớn nên khả năng hấp thu và chuyển hóa các chất trong cơ thể rất lớn. Nhờ vậy, vi sinh vật có khả năng sinh trưởng, sinh sản rất nhanh, tạo ra khối lượng sinh khối lớn. Đặc điểm khiến vi sinh vật là đối tượng được ứng dụng trong sản xuất các chế phẩm sinh học.
Để nghiên cứu quá trình ứng dụng thu sinh khối vi sinh vật đối với từng loại sản phẩm khác nhau, người ta nuôi cấy hai loài vi khuẩn Streptomyces rimosus (thu kháng sinh tetracylin) và Propionibacterium shermanii (thu vitamin B12) vào từng môi trường với điều kiện dinh dưỡng thích hợp ở 300C. Đường cong sinh trưởng của từng loài vi khuẩn và sự biến đổi về hàm lượng sản phẩm được thể hiện ở hình dưới:
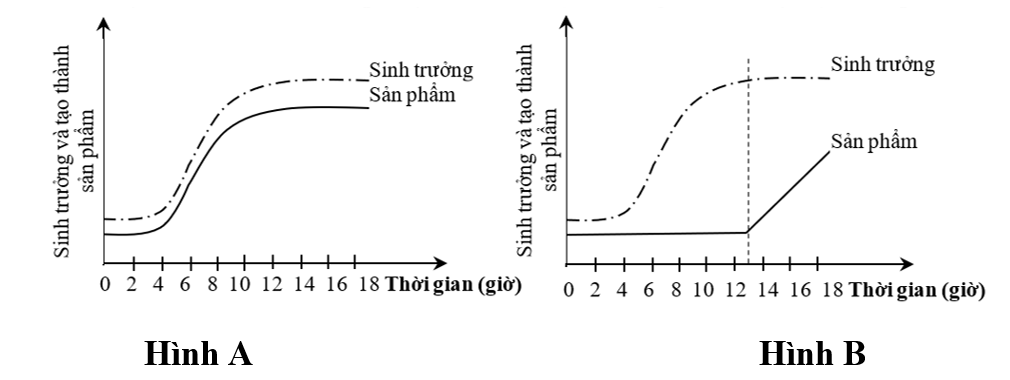
Biết rằng: Vitamin B12 là chất cần thiết cho quá trình sinh trưởng của vi khuẩn (cofactor của nhiều loại enzim tổng hợp ADN và chuyển hoá axit amin), chủ yếu được tạo ra trong giai đoạn vi khuẩn đang sinh trưởng và phát triển mạnh. Tetracylin là sản phẩm không cần thiết cho sự sinh trưởng của vi khuẩn (làm ức chế hoạt động của vi khuẩn khác và gia tăng khả năng cạnh tranh), thường được tạo ra sau khi pha sinh trưởng đã kết thúc.
Để tối ưu hiệu quả sản xuất các sản phẩm khác nhau từ các nhóm vi sinh vật khác nhau, người ta phải tiến hành các kiểu nuôi cấy trong môi trường thích hợp. Cụ thể: kháng sinh là sản phẩm tạo ra chủ yếu ở pha cân bằng nên vi sinh vật cần được nuôi cấy không liên tục để thu được lượng sản phẩm đối đa, vitamin là sản phẩm gắn liền với sự sinh trưởng, do đó muốn thu sinh khối tối đa từ vi khuẩn cần nuôi cấy trong điều kiện nuôi cấy liên tục (không có pha cân bằng, pha luỹ thừa kéo dài liên tục).
Trả lời cho các câu 88, 89, 90, 91, 92, 93, 94, 95 dưới đây:
Kéo thả các đáp án thích hợp vào chỗ trống
Vi khuẩn có kích thước nên có tỉ lệ lớn. Nhờ vậy có khả năng sinh trưởng và sinh sản , có thể thu lượng sinh khối lớn. Do đó, vi sinh vật được ứng dụng nhiều trong sản xuất các chế phẩm sinh học. Người ta nuôi cấy hai loài vi khuẩn Streptomyces rimosus để thu và Propionibacterium shermanii để thu .
Đáp án đúng là: Nhỏ; S/V; nhanh; kháng sinh Tetracylin; vitamin B12
Đọc thông tin trên bài đọc để tìm từ khóa chính xác
Đáp án cần chọn là: Nhỏ; S/V; nhanh; kháng sinh Tetracylin; vitamin B12
Kéo thả các đáp án thích hợp vào chỗ trống
- Sự sinh trưởng của vi khuẩn Streptomyces rimosus được biểu diễn ở ,
- Sự sinh trưởng của vi khuẩn Propionibacterium shermanii được biểu diễn ở
Để tối ưu hiệu quả sản xuất các sản phẩm từ hai nhóm vi sinh vật trên, người ta nuôi cấy vi khuẩn Streptomyces rimosus trong điều kiện và vi khuẩn Propionibacterium shermanii trong điều kiện
Đáp án đúng là: hình B; hình A; hình B; nuôi cấy liên tục
Phân tích đồ thì hình A và hình B, so sánh sự khác nhau giữa đường cong sinh trưởng và thời điểm sản phẩm được sản xuất với nồng độ cao.
Đáp án cần chọn là: hình B; hình A; hình B; nuôi cấy liên tục
Nhận định dưới đây là đúng hay sai?
Tỷ lệ S/V của vi sinh vật là rất lớn
Đáp án đúng là: A
Dựa vào đặc điểm về kích thước của VSV: kích thước rất nhỏ
Đáp án cần chọn là: A
Nhận định dưới đây là đúng hay sai?
Tetracylin là chất cần thiết cho quá trình sinh trưởng của vi khuẩn
Đáp án đúng là: B
Dựa vào vai trò của Tetracylin với VSV
Đáp án cần chọn là: B
Nhận định dưới đây là đúng hay sai?
Khi nuôi cấy vi sinh vật để thu sinh khối, chỉ có một kiểu môi trường nuôi cấy
Đáp án đúng là: B
Dựa vào đặc điểm về tỷ lề diện tích bề mặt / thể tích của vi sinh vật, vai trò của Tetracylin và các phương pháp nuôi cấy mà đề bài đưa ra trong đoạn văn bản.
Đáp án cần chọn là: B
Vitamin B12 là chất cần thiết cho quá trình sinh trưởng của vi khuẩn, chủ yếu được tạo ra ở thời điểm:
Đáp án đúng là: B
Đọc kỹ nội dung văn bản, quan sát và phân tích hai đồ thị mô tả quá trình nuôi cấy vi sinh vật nhằm thu vitamin B12 và thời điểm vitamin B12 được tạo ra.
Đáp án cần chọn là: B
Tetracylin được vi sinh tạo ra để làm ức chế hoạt động của vi khuẩn khác và gia tăng khả năng cạnh tranh, được tạo ra ở thời điểm:
Đáp án đúng là: B
Đọc kỹ nội dung văn bản, quan sát và phân tích hai đồ thị để tìm ra đồ thị mô tả quá trình nuôi cấy vi sinh vật nhằm thu Tetracylin và thời điểm Tetracylin được tạo ra.
Đáp án cần chọn là: B
Chọn các nhận định Đúng
Có bao nhiêu phát biểu sau đây là đúng khi nói về ứng dụng nuôi cấy vi sinh vật để thu sinh khối?
Đáp án đúng là: A; D
Đựa vào các dữ liệu trong bài đọc và thông tin được đưa ra trong đồ thị hình A và hình B để xác định tính đúng sai của các nhận định.
Đáp án cần chọn là: A; D
Dựa vào thông tin sau và trả lời 5 câu hỏi tiếp theo:
Nước thải chế biển thủy sản có chứa nhiều protein, khi protein bị thủy phân sinh ra ammonium làm cho nước thải có lượng ammonium cao. Ở dạng khí, nồng độ ammonium cao gây kích thích niêm mạc mũi, đường hô hấp dẫn đến dị ứng và tăng tiết dịch, co thắt khí quản và ho. Khi vào đường hô hấp, ammonia di chuyển từ phổi vào máu. Trong máu, ammonium bị oxy hóa tạo thành nitrite gây ức chế chức năng vận chuyển oxy của hồng cầu làm cho người bị xanh xao, nặng hơn có thể gây thiếu oxy não dẫn đến đau đầu, mệt mỏi, hôn mê thậm chí có thể tử vong.
Nghiên cứu này được thực hiện để đánh giá khả năng hấp thu ammonium của các 3 dòng vi khuẩn khác nhau, làm cơ sở cho các nghiên cứu ứng dụng để xử lý ammonium trong nước thải.
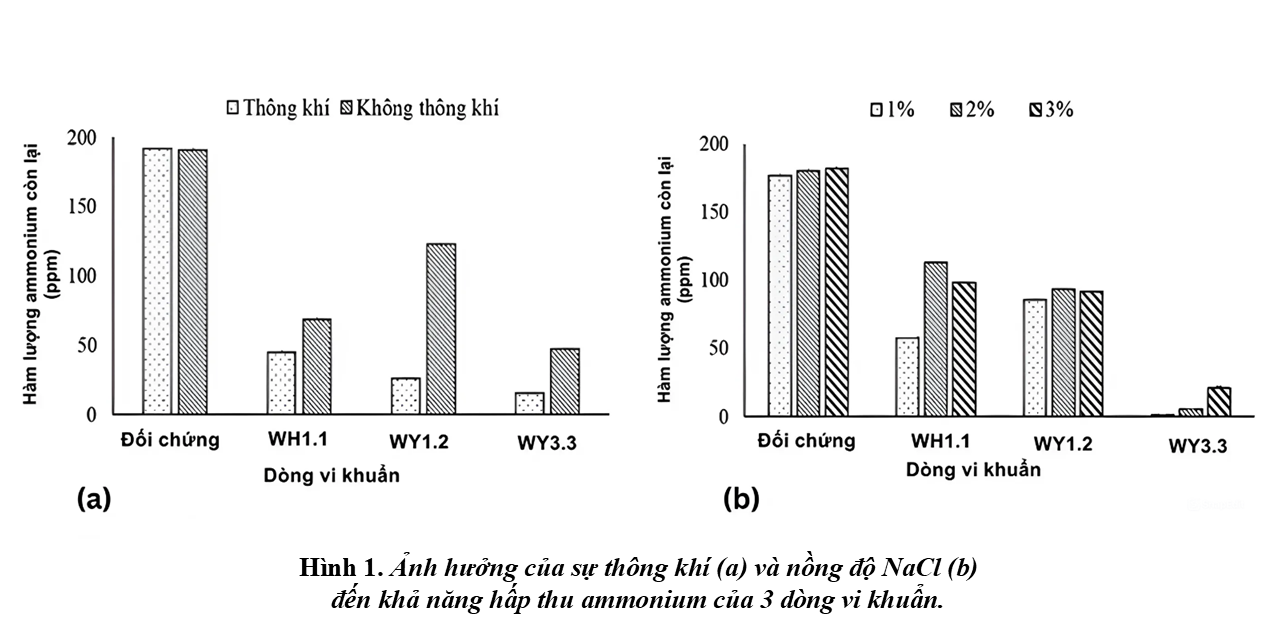
(Nguồn: Tạp chí Khoa học Đại học Cần Thơ, Tập 60, Số 1B (2024): 86-96).
Trả lời cho các câu 96, 97, 98, 99, 100 dưới đây:
Điền từ thích hợp vào chỗ trống
Trong nước thải chế biến thủy sản có chứa lượng _______ cao, vì trong nước này có chứa nhiều protein.
Đáp án đúng là: ammonium
Đọc kỹ và phân tích đoạn văn bản để tìm ra từ khóa phù hợp.
Đáp án cần điền là: ammonium
Chọn các đáp án đúng
Trong nghiên cứu này, yếu tố nào được sử dụng để đánh giá khả năng hấp thu ammonium của 3 dòng vi khuẩn.
Đáp án đúng là: A; C
Đọc kỹ văn bản và phân tích đồ thị để hiễu thí nghiệm, từ đó tìm ra các yếu tố được sử dụng để đánh giá khả năng hấp thu ammonium của 3 dòng vi khuẩn quan tâm.
Đáp án cần chọn là: A; C
Trong điều kiện không thông khí, dòng vi khuẩn nào có khả năng hấp thu ammonia tốt nhất?
Đáp án đúng là: D
- Quan sát biểu đồ mô tả ảnh hưởng của sự thông khí đến khả năng hấp thu ammonium.
- Tìm dòng vi khuẩn có hàm lượng ammonium còn lại thấp nhất trong điều kiện không thông khí.
Đáp án cần chọn là: D
Kéo thả đáp án chính xác vào chỗ trống
Dòng vi khuẩn đã hấp thu khoảng 75% ammonium trong điều kiện nồng độ NaCl 1% .
Đáp án đúng là: WH1.1
- Dựa vào biểu đồ về ảnh hưởng của nồng độ NaCl đến khả năng hấp thu ammonium của các dòng vi khuẩn.
- Xác định dòng vi khuẩn hấp thu 75% ammonium.
Đáp án cần chọn là: WH1.1
Để xử lí ammonium trong nước thải thủy sản thì cần dùng dòng vi khuẩn tương ứng với điều kiện nào phù hợp nhất?
Đáp án đúng là: D
Quan sát biểu đồ để tìm dòng vi khuẩn hấp thu ammonium tốt nhất trong điều kiện không thông khí và nồng độ NaCl 1%.
Đáp án cần chọn là: D